山西省太原市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-22 类型:期中考试
一、单选题
-
1. 一元二次方程(x﹣1)(x﹣2)=0的解是( )A、x=1 B、x=2 C、x1=1,x2=2 D、x1=﹣1,x2=﹣22. 若直角三角形的斜边长为12,则斜边上的中线长为( )A、6 B、8 C、10 D、123. 不透明的袋子中装有红球1个、绿球1个、白球2个,除颜色外无其他差别.随机摸出一个小球后不放回,再摸出一个球,则两次都摸到白球的概率是( )A、 B、 C、 D、4. 如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
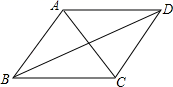 A、①③ B、②③ C、③④ D、①②③5. 下列性质中,平行四边形,矩形,菱形,正方形共有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分内角6. 根据下列表格的对应值:
A、①③ B、②③ C、③④ D、①②③5. 下列性质中,平行四边形,矩形,菱形,正方形共有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分内角6. 根据下列表格的对应值:x
…
6.17
6.18
6.19
6.20
…
ax2+bx+c
…
-0.02
-0.01
0.01
0.04
…
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)一个解x的取值范围是( )
A、6<x<6.17 B、6.17<x<6.18 C、6.18<x<6.19 D、6.19<x<6.207. 某学习小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示折线统计图,则符合这一结果的试验最有可能的是( ) A、不透明袋中装有大小和质地都相同的1个红球和2个黄球,从中随机取一个,取到红球 B、任意写一个整数,它能被2整除 C、掷一枚正六面体的骰子,出现1点朝上 D、先后两次掷一枚质地均匀的硬币,两次都出现反面8. 如图,在正方形ABCD中,点E、点F分别在AD、CD上,且AE=DF,若四边形OEDF的面积是1,OA的长为1,则正方形的边长AB为( )
A、不透明袋中装有大小和质地都相同的1个红球和2个黄球,从中随机取一个,取到红球 B、任意写一个整数,它能被2整除 C、掷一枚正六面体的骰子,出现1点朝上 D、先后两次掷一枚质地均匀的硬币,两次都出现反面8. 如图,在正方形ABCD中,点E、点F分别在AD、CD上,且AE=DF,若四边形OEDF的面积是1,OA的长为1,则正方形的边长AB为( ) A、1 B、2 C、 D、29. 将一条长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各自做成一个正方形,若两个正方形的面积之和为12.5 cm2 , 则这两段铁丝的长度是( )A、5 cm,15 cm B、12 cm,8 cm C、4 cm,16 cm D、10 cm,10 cm10. 定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )
A、1 B、2 C、 D、29. 将一条长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各自做成一个正方形,若两个正方形的面积之和为12.5 cm2 , 则这两段铁丝的长度是( )A、5 cm,15 cm B、12 cm,8 cm C、4 cm,16 cm D、10 cm,10 cm10. 定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.如图,在平面直角坐标系xOy中,矩形OABC的边OA=3,OC=4,点M(2,0),在边AB存在点P,使得△CMP为“智慧三角形”,则点P的坐标为( )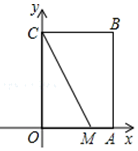 A、(3,1)或(3,3) B、(3,)或(3,3) C、(3,)或(3,1) D、(3,)或(3,1)或(3,3)
A、(3,1)或(3,3) B、(3,)或(3,3) C、(3,)或(3,1) D、(3,)或(3,1)或(3,3)二、填空题
-
11. 如果一个直角三角形斜边上的中线长为6.5cm,一条直角边长为5cm,则另一条直角边的长为cm.12. 若关于x的一元二次方程x2-mx-n=0有一个根是2,则2m+n= .13. 在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球不放回,再随机地摸出一个小球,则两次摸出的小球的标号的和为奇数的概率是.
14. 如图,要设计一幅宽25cm,长40cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比是2∶3,如果要使彩条所占面积是图案面积的 , 设每个横彩条的宽度是2xcm.则根据题意可列方程为 .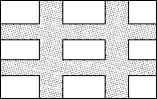 15. 如图,在矩形ABCD中,AB=6,BC=8.如果?、F分别是AD、BC上的点,且EF经过AC中点O,G,H是对角线AC上的点.下列判断正确的有 .
15. 如图,在矩形ABCD中,AB=6,BC=8.如果?、F分别是AD、BC上的点,且EF经过AC中点O,G,H是对角线AC上的点.下列判断正确的有 .①在AC上存在无数组G、H,使得四边形EGFH是平行四边形;②在AC上存在无数组G、H,使得四边形EGFH是矩形;③在AC上存在无数组G、H,使得四边形EGFH是菱形;④当AG=时,存在E、F、G,H,使得四边形EGFH是正方形.

三、解答题
-
16. 用适当的方法解方程.(1)、x2-6x+2=0;(2)、(2x+5)-3x(2x+5)=0.17. 如图,正方形ABCD的对角线AC与BD交于点O.过点C作CE∥BD,过点D作DE∥AC,CE与DE交于点E,求证:DE=CE.
 18. 2020年某县投入100万元用于农村“扶贫工程”,计划以后每年以相同的增长率投入,2022年该县计划投入“扶贫工程”144万元.(1)、求该县投入“扶贫工程”的年平均增长率;(2)、若2023年保持从2020年到2022年的年平均增长率不变,求2023年该县将投入“扶贫工程”多少万元.19. 中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是我国古代数学的重要文献.
18. 2020年某县投入100万元用于农村“扶贫工程”,计划以后每年以相同的增长率投入,2022年该县计划投入“扶贫工程”144万元.(1)、求该县投入“扶贫工程”的年平均增长率;(2)、若2023年保持从2020年到2022年的年平均增长率不变,求2023年该县将投入“扶贫工程”多少万元.19. 中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是我国古代数学的重要文献.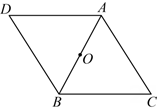 (1)、小聪想从这4部数学名著中随机选择1部阅读,则他选中《九章算术》的概率为;(2)、某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,求恰好选中《九章算术》和《孙子算经》的概率.20. 如图,在矩形ABCD中,AB=12 cm,BC=6 cm.点P沿AB边从点A开始向点B以2 cm/s的速度移动,点Q沿DA边从点D开始向点A以1 cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间(0<t<6),那么当t为何值时,△QAP的面积等于8 cm2?
(1)、小聪想从这4部数学名著中随机选择1部阅读,则他选中《九章算术》的概率为;(2)、某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,求恰好选中《九章算术》和《孙子算经》的概率.20. 如图,在矩形ABCD中,AB=12 cm,BC=6 cm.点P沿AB边从点A开始向点B以2 cm/s的速度移动,点Q沿DA边从点D开始向点A以1 cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间(0<t<6),那么当t为何值时,△QAP的面积等于8 cm2?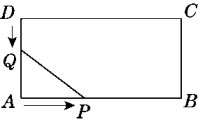 21. 如图,四边形ABCD和四边形CEFG都是正方形,连接BG、DE.求证:
21. 如图,四边形ABCD和四边形CEFG都是正方形,连接BG、DE.求证: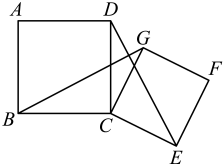 (1)、BG=DE;(2)、BG⊥DE.22. 2020东京奥运会于今年7月23日至8月8日举行,奥林匹克官方旗舰店在7月份推出了A和B两款奥运吉祥物公仔.7月份,两款公仔共售出了1500个,其中B款的销量不低于A款销量的2倍.(1)、7月份,店家卖出的B款公仔至少有多少个?(2)、已知7月份,A款的价格为56元/个,B款的价格为50元/个,且B款的销量恰好为(1)中的最小值.8月份,为了提高销量,A款的售价比7月份的售价下降了a%,销量与7月份相同;B款的售价比7月份的售价下降了a%,销量比7月份增加了a%,结果8月份两款公仔的总销售额为78000元,求a的值.23. 如图1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC.
(1)、BG=DE;(2)、BG⊥DE.22. 2020东京奥运会于今年7月23日至8月8日举行,奥林匹克官方旗舰店在7月份推出了A和B两款奥运吉祥物公仔.7月份,两款公仔共售出了1500个,其中B款的销量不低于A款销量的2倍.(1)、7月份,店家卖出的B款公仔至少有多少个?(2)、已知7月份,A款的价格为56元/个,B款的价格为50元/个,且B款的销量恰好为(1)中的最小值.8月份,为了提高销量,A款的售价比7月份的售价下降了a%,销量与7月份相同;B款的售价比7月份的售价下降了a%,销量比7月份增加了a%,结果8月份两款公仔的总销售额为78000元,求a的值.23. 如图1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC. (1)、探究PG与PC的位置关系及的值;(写出结论,不需要证明)(2)、如图2,将原问题中的正方形ABCD和正方形BEFC换成菱形ABCD和菱形BEFG,且∠ABC=∠BEF=60°,探究PG与PC的位置关系及的值.写出你的猜想并加以证明;(3)、如图3,将图2中的菱形BEFG绕点B顺时针旋转.使菱形BEFG的边BG恰好与菱形ABCD的边AB在同一条直线上,问题(2)中的其他条件不变,你在(2)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(1)、探究PG与PC的位置关系及的值;(写出结论,不需要证明)(2)、如图2,将原问题中的正方形ABCD和正方形BEFC换成菱形ABCD和菱形BEFG,且∠ABC=∠BEF=60°,探究PG与PC的位置关系及的值.写出你的猜想并加以证明;(3)、如图3,将图2中的菱形BEFG绕点B顺时针旋转.使菱形BEFG的边BG恰好与菱形ABCD的边AB在同一条直线上,问题(2)中的其他条件不变,你在(2)中得到的两个结论是否发生变化?写出你的猜想并加以证明.