山西省临汾市尧都区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图案中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知点A(m，2)与点B(-6，n)关于原点对称，则m-n的值为（）

A、4 B、-8 C、8 D、-4

查看试题解析
3. 若 $y = (a + 1) x^{| a + 3 |} - x + 3$ 是关于x的二次函数，则a的值是（）

A、1 B、-5 C、-1 D、-5或-1

查看试题解析
4. 一元二次方程 $x^{2} - 4 x + 5 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
5. 已知二次函数 $y = a x^{2} + b x + c$ 的部分图像如图所示，当y>0时，x的取值范围是（）

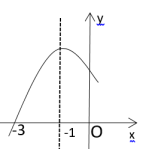A、x>-3 B、-3<x<1 C、x<-3或x>1 D、x<1

查看试题解析
6. 如果三点 $P_{1} (- 1 ， y_{1}) ， P_{2} (1 ， y_{2})$ 和 $P_{3} (5 ， y_{3})$ 在抛物线 $y = - x^{2} + 5 x + c$ 的图象上，那么 $y_{1} ， y_{2} ， y_{3}$ 之间的大小关系是（）

A、 $y_{3} < y_{1} < y_{2}$ B、 $y_{2} < y_{3} < y_{1}$ C、 $y_{1} < y_{3} < y_{2}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
7. 如图所示，点A、B、C、D都在方格纸的格点上，若△COD绕点O按顺时针方向旋转到△AOB的位置，则旋转的角度为（）

A、30° B、45° C、60° D、90°

查看试题解析
8. 把 $y = 2 x^{2} + 8 x + 5$ 配方成 $y = 2 {(x - h)}^{2} + k$ 的形式后，h和k对应的值分别是（）

A、-2，-3 B、2，-3 C、2，3 D、-2，3

查看试题解析
9. 2021年是中国共产党成立100周年，山西某中学发起了“热爱祖国，感恩共产党”说句心里话征集活动，学校学生会主席要求征集活动在微信朋友圈里进行传递，规则为：将征集活动发在自己的朋友圈，再邀请n个好友转发征集活动，每个好友转发朋友圈，又分别邀请n个互不相同的好友转发征集活动，以此类推，已知经过两轮传递后，共有1641人参与了传递活动，则方程列为（）

A、 ${(1 + n)}^{2} = 1641$ B、 $1 + (n + 1) + {(n + 1)}^{2} = 1641$ C、 $n + n^{2} = 1641$ D、 $1 + n + n^{2} = 1641$

查看试题解析
10. 如图， $⊙ A$ 过点O、D、C、B四点，连接CO，CD，已知 $∠ D C O = 30 °$ ， $B (4 ， 0)$ ，则D点坐标为（）

A、 $(0 ， 2)$ B、 $(0 ， \frac{4 \sqrt{3}}{3})$ C、 $(0 ， \frac{8 \sqrt{3}}{3})$ D、 $(0 ， 3)$

查看试题解析

二、填空题

11. 抛物线 $y = - 3 x^{2} + 6$ 的顶点坐标为．

查看试题解析
12. 如图，AB是圆O的直径，BC、CD是弦，OC是∠BCD的平分线，若∠BAD＝80°，则∠OCB的度数是．

查看试题解析
13. 抛物线 $y = (k + 1) x^{2} - x - 2$ 与x轴有交点，则k的取值范围是．

查看试题解析
14. 如图，四边形ABCD内接于圆O，∠BOD=116°，则∠BCD的度数是．

查看试题解析
15. 如图，山西汾河大桥十号线桥可以近似地看作直径为500m的圆弧，桥拱和路面之间用数根钢索垂直相连，其正下方的路面AB长度为300m，那么这些钢索中最长的一根为．

查看试题解析

三、解答题

16.

(1)、解方程： $2 x^{2} - 4 x - 3 = 0$ ．

(2)、下面是大壮同学进行解方程的过程，请你认真阅读并完成相应任务：
解方程： $4 {(2 y - 5)}^{2} = 9 {(3 y - 1)}^{2}$ ．
解： $4 {(2 y - 5)}^{2} - 9 {(3 y - 1)}^{2} = 0$ ， ……第一步
$[(4 y - 10) + (9 y - 3)] [(4 y - 10) - (9 y - 3)] = 0$ ， ……第二步
$(13 y - 13) (5 y - 7) = 0$ ， ……第三步
$13 y - 13 = 0$ 或 $5 y - 7 = 0$ ， ……第四步
解得： $y_{1} = 1$ ， $y_{2} = \frac{7}{5}$ ． ……第五步
任务一：①以上解方程过程中，主要是依据      ▲ 来求解的（填“配方法”或“公式法”或“因式分解法”）．
②第      ▲ 步开始出现错误，错误的原因是      ▲ ．
任务二：请直接写出本题的正确结果．

查看试题解析
17. 如图，正方形ABCD与正方形A₁B₁C₁D₁关于某点中心对称，已知A， $A_{1} ， B_{1}$ 三点的坐标分别是（0，5），（0，1），（3，1）．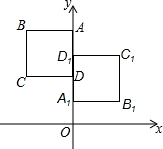

(1)、求对称中心的坐标．

(2)、写出顶点D，B， $D_{1} ， C_{1}$ 的坐标．

查看试题解析
18. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC(顶点是网格线的交点) ，线段MN在网格线上．

⑴画出△ABC关于线段MN所在直线对称的△DEF．

⑵将线段AB绕点C顺时针旋转90°，得到线段GH，画出线段GH．

查看试题解析
19. 太谷壶瓶枣，是山西省太谷区特产，传说在春秋战国时期就有栽培，果实大，以形似“壶”
状而得名．红枣味甜可口，营养丰富，保健医疗价值很高，民间有“每日食三枣，一辈子不显老”的说法，长期食用，对增进人体健康有重要作用．某经销商销售一种新品种壶瓶枣，这种新品种进价每千克50元(规定每千克销售利润不低于5元且不高于30元)，现在以75元/千克的售价卖出，则每周可卖出80千克．该经销商通过对当地市场调查发现：若每千克降价5元，则每周多卖出20千克；因疫情原因，该经销商决定暂时降价销售，设每千克销售价降低x元，每周销售利润为y元．

(1)、当售价为每千克65元时，每周销售量为千克，利润为元．

(2)、求y与x之间的函数关系式并写出自变量x的取值范围．

(3)、当销售单价定为多少元时，该经销商每周可获得最大利润？最大利润是多少元？

查看试题解析
20. 阅读与思考
请阅读下列材料，并完成相应的任务：
阿尔·花拉子米(约780~约850)，著名阿拉伯数学家、天文学家、地理学家，是代数与算术的整理者，被誉为“代数之父”．他利用正方形图形巧妙解出了一元二次方程 $x^{2} + 2 x - 35 = 0$ 的一个解．将边长为x的正方形和边长为1的正方形，外加两个长方形，长为x，宽为1，拼合在一起面积就是 $x^{2} + 2 x \times 1 + 1^{2}$ ，即 $x^{2} + 2 x + 1$ ，而由原方程 $x^{2} + 2 x - 35 = 0$ 变形得 $x^{2} + 2 x + 1 = 35 + 1$ ，即边长为x+1的正方形面积为36．所以 ${(x + 1)}^{2} = 36$ ，则x=5．
任务：

(1)、上述求解过程中所用的方法与下列哪种方法是一致的（）

A、直接开平方法 B、公式法 C、配方法 D、因式分解法

(2)、所用的数学思想方法是（）

A、分类讨论思想 B、数形结合思想 C、建模思想 D、整体思想

(3)、运用上述方法构造出符合方程 $x^{2} + 6 x - 7 = 0$ 的一个正根的正方形(画出拼接的正方形并求出正根)．

查看试题解析
21. 如图，CD为圆O的直径，CD⊥AB，垂足为F，AO⊥BC，垂足为E，连接AC．

(1)、求∠B的度数．

(2)、若 $C E = 4 \sqrt{3}$ ，求圆O的半径．

查看试题解析
22. 综合与实践
问题情境：数学活动课上，老师要求学生出示两个大小不一样的等腰直角三角形，如图1所示，把Rt△ADE和Rt△ABC摆在一起，其中直角顶点A重合，延长CA至点F ，满足AF=AC，然后连接DF、BE．

(1)、实践猜想：
图1中的BE与DF的数量关系为：，位置关系为：．

(2)、猜想证明：
当△ADE绕着点A顺时针旋转一定角度α（0＜α＜90°）时，如图2所示，（1）中的结论是否还成立?若成立，请写出证明过程，若不成立，请说明理由．

(3)、问题解决：
若 $B C = 4 \sqrt{2} ， D E = 2 \sqrt{2}$ ， △ADE绕着点A顺时针旋转一定角度α（0＜α＜360°）的过程中，求BE的最大值与最小值．

查看试题解析
23. 综合与探究
如图，开口向下的抛物线y=ax²+bx+c与x轴交于点A(-3，0)、C(1，0)，与y轴交于点B(0，3)，连接AB．

(1)、求抛物线解析式．

(2)、若P为线段AB上一点，且AP=2 $\sqrt{2}$ ，求点P的坐标．

(3)、在(2)的条件下，设M是y轴上一点，试探究：抛物线上是否存在点N，使得以A，P，M，N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析