山西省晋城市高平市2020-2021学年九年级上学期期中数学测试卷

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 化简 $\sqrt{12}$ 的结果是（）

A、 $3 \sqrt{2}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $2 \sqrt{2}$

查看试题解析
2. 若 $\frac{a - b}{b} = \frac{3}{5}$ ，则 $\frac{a}{b}$ 的值为（）

A、 $\frac{8}{5}$ B、 $\frac{5}{3}$ C、 $\frac{3}{5}$ D、 $\frac{5}{8}$

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{(- 5)^{2}} = \pm 5$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{8} \div \sqrt{2} = 4$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$

查看试题解析
4. 下列说法中正确的是（）

A、两个直角三角形相似 B、两个等腰三角形相似 C、两个等边三角形相似 D、两个锐角三角形相似

查看试题解析
5. 下列方程没有实数根的是（）

A、 $x^{2} - 7 x - 18 = 0$ B、 $x^{2} + 1 = 4 x$ C、 $x^{2} - 2 x + 3 = 0$ D、 $(x - 2) x = 12$

查看试题解析
6. 如图，网格中的两个三角形是位似图形，它们的位似中心是（）

A、点A B、点B C、点C D、点D

查看试题解析
7. 若 $x = 1$ 是一元二次方程 $(m + 3) x^{2} - m x + m^{2} - 12 = 0$ 的其中一个解，则 $m$ 的值为（）

A、3 B、-3 C、±3 D、2

查看试题解析
8. 若矩形ABCD∽矩形EFGH，相似比为2：3，已知AB＝4cm，BC＝5cm，则矩形EFGH的周长是（）

A、12cm B、27cm C、24cm D、18cm

查看试题解析
9. 已知在 $Δ A B C$ 中， $∠ A = 78 ° ， A B = 4 ， A C = 6$ ，下列阴影部分的三角形与原 $Δ A B C$ 不相似的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在平面直角坐标系中，将正方形OABC绕点O逆时针45°后得到正方形 $O A_{1} B_{1} C_{1}$ ，依次方式，将正方形 $O A B C$ 绕点O连续旋转2021次得到正方形 $O A_{2021} B_{2021} C_{2021}$ ，如果点C的坐标为 $(0 ， 1)$ ，那么点 $B_{2021}$ 的坐标为（）

A、 $(- 1 ， 1)$ B、 $(- \sqrt{2} ， 0)$ C、 $(0 ， - \sqrt{2})$ D、 $(1 ， 0)$

查看试题解析

二、填空题

11. 计算： $(\sqrt{3} + 1) (\sqrt{3} - 1)$ =.

查看试题解析
12. 如图，若四边形ABCD∽四边形EFGH，则 $∠ α$ 的度数为．

查看试题解析
13. 现要在一个长为35m，宽为22m的矩形花园中修建等宽的小道，剩余的地方种植花草，如图，要使种植花草的面积为625m²，设小道的宽为xm，则根据题意，可列方程为．

查看试题解析
14. 如图，在 $Δ A B C$ 中，DE//BC， $G$ 为 $B C$ 上一点，连接 $A G$ 交 $D E$ 于点 $F$ ，已知 $A F = 2$ ， $A G = 6$ ， $E C = 5$ ，则 $A C$ = ．

查看试题解析
15. 如图， $P$ 为平行四边形 $A B C D$ 边 $B C$ 上一点， $E ， F$ 分别为 $P A ， P D$ 上的点，且 $D F = 3 P F ， A E = 3 P E$ ， $Δ P E F ， Δ P D C ， Δ P A B$ 的面积分别为 $S ， S_{1} ， S_{2}$ ，若 $S = 3$ ，则 $S_{1} + S_{2}$ = ．

查看试题解析

三、解答题

16.

(1)、计算： $(\sqrt{5} - \sqrt{2})^{2} + \sqrt{40}$

(2)、解方程： $2 x^{2} - 7 x + 6 = 0$

查看试题解析
17. 如图，在 $Δ A B C$ 中， $∠ B A E = ∠ C A E$ ， $B E ⊥ A E$ 于点 $E$ ， $B E$ 的延长线交 $A C$ 于点 $D$ ， $F$ 是 $C D$ 的中点，求证： $E F = \frac{1}{2} B C$ ．

查看试题解析
18. 如图，在四边形ABCD中，AD∥BC，∠BAD＝90°，且 $B D ⊥ D C$ ．

(1)、△ABD与△DCB相似吗？请说明理由；

(2)、若AD＝4，BC＝9，请求出BD的长．

查看试题解析
19. 如图，在平面直角坐标系中，给出了格点△ABC（顶点式网格线的交点），已知点B的坐标为（1，2）．
⑴画出△ABC关于 $y$ 轴对称的△ $A_{1} B_{1} C_{1}$ ，并写出 $C_{1}$ 的坐标；
⑵在给定的网格中，以点O为位似中心，将△ $A_{1} B_{1} C_{1}$ 作位似变换且放大到原来的两倍，得到△ $A_{2} B_{2} C_{2}$ ，画出△ $A_{2} B_{2} C_{2}$ ；并写出点 $B_{2}$ 的坐标．

查看试题解析
20. 阅读下面问题： $\frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ ； $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ； $\frac{1}{\sqrt{5} + 2} = \sqrt{5} - 2$ ．

(1)、根据以上规律，化简： $\frac{1}{\sqrt{11} + \sqrt{10}} =$ ；

(2)、 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ （ $n$ 为正整数）=；

(3)、比较 $\sqrt{23} - \sqrt{22}$ 和 $\sqrt{22} - \sqrt{21}$ 的大小．

查看试题解析
21. 某饮料批发商店平均每天可售出某款饮料300瓶，售出1瓶该款饮料的利润是1元.经调查发现，若该款饮料的批发价每降低0.1元，则每天可多售出100瓶.为了使每天获得的利润更多，该饮料批发商店决定降价 $x$ 元．

(1)、当 $x$ 为多少时，该饮料批发商店每天卖出该款饮料的利润为400元？

(2)、该饮料批发商店每天卖出该款饮料的利润能达到600元吗？若能，请求出 $x$ 的值，若不能，请说明理由．

查看试题解析
22. 综合与实践
某“综合与实践”小组开展了测量本校旗杆高度的实践活动，他们制定了测量方案，并利用课余时间完成了实地测量．他们在旗杆底部所在的平面上，放置一个平面镜E．来测量学校旗杆的高度，当镜子中心与旗杆的距离 $E B = 20$ 米，镜子中心与测量者的距离 $E D = 2$ 米时，测量者刚好从镜子中看到旗杆的顶端点A．已知测量者的身高为1.6米，测量者的眼睛距地面的高度为1.5米，求学校旗杆的高度是多少米．
任务一：在计算过程中C，D之间的距离应该是 ▲ 米．
任务二：根据以上测量结果，请你帮助“综合与实践”小组求出学校旗杆AB的高度．
任务三：该“综合与实践”小组在制定方案时，讨论过“利用测量者在阳光下的影子测量旗杆的高度”的方案，请你在备用图中画出该方案的示意图，并说明必要的已知条件．

查看试题解析
23. 如图，将矩形纸片ABCD（AD＞DC）的∠A沿着过点D的直线折叠，使点A落在BC边上，落点为E，折痕交AB边于点F．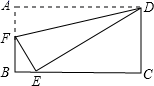

(1)、图中的全等三角形是，相似三角形是．

(2)、若BE：EC＝1：4，CD＝9，求BF的长；

(3)、若BE：EC＝m：n，求AF：FB．（用含有m，n的代数式表示）

查看试题解析