内蒙古自治区赤峰市松山区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-22 类型:期中考试
一、单选题
-
1. 方程的解为( )A、 , B、 , C、 , D、2. 若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是( )A、
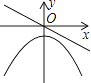 B、
B、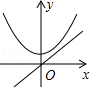 C、
C、 D、
D、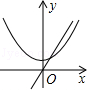 3. 下列图形是中心对称图形的是( )A、
3. 下列图形是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )A、1 B、﹣1 C、1或﹣1 D、5. 抛物线 的顶点坐标是( )A、 B、 C、 D、6. 学生冬季运动装原来每套的售价是100元,后经连续两次降价,现在的售价是81元,则平均每次降价的百分数是( )A、9% B、8.5% C、9.5% D、10%7. 若 , , 为二次函数 的图象上的三点,则 , , 的大小关系是 .A、 B、 C、 D、8. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确的个数是( )
4. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )A、1 B、﹣1 C、1或﹣1 D、5. 抛物线 的顶点坐标是( )A、 B、 C、 D、6. 学生冬季运动装原来每套的售价是100元,后经连续两次降价,现在的售价是81元,则平均每次降价的百分数是( )A、9% B、8.5% C、9.5% D、10%7. 若 , , 为二次函数 的图象上的三点,则 , , 的大小关系是 .A、 B、 C、 D、8. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确的个数是( )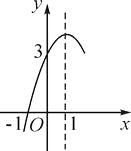 A、4个 B、3个 C、2个 D、1个9. 西宁中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
A、4个 B、3个 C、2个 D、1个9. 西宁中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为米,在如图所示的坐标系中,这个喷泉的函数关系式是( ) A、y=-(x-)2+3 B、y=-3(x+)2+3 C、y=-12(x-)2+3 D、y=-12(x+)2+310. 把边长为3的正方形 绕点A顺时针旋转45°得到正方形 ,边 与 交于点O,则四边形 的周长是( )
A、y=-(x-)2+3 B、y=-3(x+)2+3 C、y=-12(x-)2+3 D、y=-12(x+)2+310. 把边长为3的正方形 绕点A顺时针旋转45°得到正方形 ,边 与 交于点O,则四边形 的周长是( ) A、6 B、 C、 D、11. 如图,将△OAB绕点O逆时针旋转到△OA'B',点B恰好落在边A'B'上.已知AB=4cm,BB'=1cm,则A'B的长是( )
A、6 B、 C、 D、11. 如图,将△OAB绕点O逆时针旋转到△OA'B',点B恰好落在边A'B'上.已知AB=4cm,BB'=1cm,则A'B的长是( ) A、1cm B、2cm C、3cm D、4cm12. 已知关于x的方程x2+2x+m=0有两个不相等的实数根,则m的取值范围是( )A、m=1 B、m≥1 C、m<1 D、m<1且m≠013. 如图,在长 ,宽 的矩形花园中,欲修宽度相等的观赏路(阴影部分),要使观赏路面积占总面积的 ,则路宽 应满足的方程是( ).
A、1cm B、2cm C、3cm D、4cm12. 已知关于x的方程x2+2x+m=0有两个不相等的实数根,则m的取值范围是( )A、m=1 B、m≥1 C、m<1 D、m<1且m≠013. 如图,在长 ,宽 的矩形花园中,欲修宽度相等的观赏路(阴影部分),要使观赏路面积占总面积的 ,则路宽 应满足的方程是( ). A、 B、 C、 D、14. 如图,D、E是等边的BC边和AC边上的点, , AD与EE相交于P点,则的度数是( )
A、 B、 C、 D、14. 如图,D、E是等边的BC边和AC边上的点, , AD与EE相交于P点,则的度数是( ) A、45° B、55° C、60° D、75°
A、45° B、55° C、60° D、75°二、填空题
-
15. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .16. 已知p,q是方程的两根,则代数式的值为 .17. 已知x能使得 + 有意义,则点P(x+2,x﹣3)关于原点的对称点P′在第象限.18. 某厂今年一月份新产品的研发资金为1000元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=
三、解答题
-
19. 先化简,再求值: , 其中20. 作图并完成解答:
 (1)、在平面直角坐标系中,点A的坐标是 , 在x轴上任取一点M,完成下列作图步骤:①连接AM,作线段M的垂直平分线 , (要求尺规作图,保留作图痕迹)过M作x轴的垂线 , 记 , 的交点为P.②在x轴上多次改变点M的位置,用①的方法得到相应的点P,把这些点用平滑的曲线连接起来.(2)、对于曲线上的任意一点P,线段PA与PM有什么关系?设点P的坐标是 , 求y与x的函数关系式.21. 已知二次函数 .(1)、用配方法将解析式化为的形式;(2)、求这个函数图象与x轴的交点坐标.22. 某网店销售某款童装,每件售价60元,每星期可卖300件.为了促销,该店决定降价销售,市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元.设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定多少元时,每星期的销售利润最大,最大利润是多少?23. 已知关于x的方程 , 试按要求解答下列问题:(1)、当该方程有一根为1时,试确定m的值;(2)、当该方程有两个不相等的实数根时,试确定m的取值范围.(3)、若m是符合条件的最大整数,求此时方程的根.24. 阅读理解:
(1)、在平面直角坐标系中,点A的坐标是 , 在x轴上任取一点M,完成下列作图步骤:①连接AM,作线段M的垂直平分线 , (要求尺规作图,保留作图痕迹)过M作x轴的垂线 , 记 , 的交点为P.②在x轴上多次改变点M的位置,用①的方法得到相应的点P,把这些点用平滑的曲线连接起来.(2)、对于曲线上的任意一点P,线段PA与PM有什么关系?设点P的坐标是 , 求y与x的函数关系式.21. 已知二次函数 .(1)、用配方法将解析式化为的形式;(2)、求这个函数图象与x轴的交点坐标.22. 某网店销售某款童装,每件售价60元,每星期可卖300件.为了促销,该店决定降价销售,市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元.设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定多少元时,每星期的销售利润最大,最大利润是多少?23. 已知关于x的方程 , 试按要求解答下列问题:(1)、当该方程有一根为1时,试确定m的值;(2)、当该方程有两个不相等的实数根时,试确定m的取值范围.(3)、若m是符合条件的最大整数,求此时方程的根.24. 阅读理解:转化思想是常用的数学思想之一.在研究新问题或复杂问题时,常常把问题转化为熟悉的或比较简单的问题来解决.如解一元二次方程是转化成一元一次方程来解决的;解分式方程是转化为整式方程来解决的.由于“去分母”可能产生增根,所以解分式方程必须检验.
利用转化思想,我们还可以解一些新的方程,如无理方程(根号下含有未知数的方程).解无理方程关键是要去掉根号,可以将方程适当变形后两边同时平方,将其转化为整式方程.由于“去根号”可能产生增根,所以解无理方程也必须检验.
例如:解方程
解:两边平方得:
解得: ,
经检验, 是原方程的根,
代入原方程中不合理,是原方程的增根.
∴原方程的根是 .
解决问题:
(1)、填空:已知关于x的方程 有一个根是 ,那么a的值为;(2)、求满足 的x的值;(3)、代数式 的值能否等于8 ? 若能,求出 的值;若不能,请说明理由.25. 如图1,点O为正方形ABCD的中心. (1)、将线段OE绕点O逆时针方向旋转90°,点E的对应点为点F,连结EF,AE,BF,请依题意补全图1;(2)、根据图1中补全的图形,猜想并证明AE与BF的关系;(3)、如图2,点G是OA中点,是等腰直角三角形,H是EF的中点, , , , 绕G点逆时针方向旋转角度,请直接写出旋转过程中BH的最大值.26. 如图,平面直角坐标系xOy中,直线AC分别交坐标轴于A,C(8,0)两点,AB∥x轴,B(6,4).
(1)、将线段OE绕点O逆时针方向旋转90°,点E的对应点为点F,连结EF,AE,BF,请依题意补全图1;(2)、根据图1中补全的图形,猜想并证明AE与BF的关系;(3)、如图2,点G是OA中点,是等腰直角三角形,H是EF的中点, , , , 绕G点逆时针方向旋转角度,请直接写出旋转过程中BH的最大值.26. 如图,平面直角坐标系xOy中,直线AC分别交坐标轴于A,C(8,0)两点,AB∥x轴,B(6,4). (1)、求过B,C两点的抛物线y=ax2+bx+4的表达式;(2)、点P从C点出发以每秒1个单位的速度沿线段CO向O点运动,同时点Q从A点出发以相同的速度沿线段AB向B点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t秒.当t为何值时,四边形BCPQ为平行四边形;(3)、若点M为直线AC上方的抛物线上一动点,当点M运动到什么位置时,△AMC的面积最大?求出此时M点的坐标和△AMC的最大面积.
(1)、求过B,C两点的抛物线y=ax2+bx+4的表达式;(2)、点P从C点出发以每秒1个单位的速度沿线段CO向O点运动,同时点Q从A点出发以相同的速度沿线段AB向B点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为t秒.当t为何值时,四边形BCPQ为平行四边形;(3)、若点M为直线AC上方的抛物线上一动点,当点M运动到什么位置时,△AMC的面积最大?求出此时M点的坐标和△AMC的最大面积.