内蒙古乌海市海南区2020-2021学年九年级上学期期中考试数学试题

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 方程 $x^{2} - 3 = 0$ 的根是（）

A、 $\sqrt{3}$ B、 $- \sqrt{3}$ C、 $\frac{1}{2}$ D、3

查看试题解析
2. 在俄罗斯方块游戏中，已拼好的图案如图所示，现又出现一小方格体正向下运动，为了使所有图案消失，你必须进行以下哪项操作，才能拼成一个完整图案，使其自动消失（）

A、顺时针旋转 $9 0^{∘}$ ，向右平移 B、逆时针旋转 $9 0^{∘}$ ，向右平移 C、顺时针旋转 $9 0^{∘}$ ，向下平移 D、逆时针旋转 $9 0^{∘}$ ，向下平移

查看试题解析
3. 对于二次函数y=﹣x2﹣1的二次项系数a，一次项系数b，常数项c描述正确的是（）

A、a=﹣1，b=﹣1，c=0 B、a=﹣1，b=0，c=1 C、a=﹣1，b=0，c=﹣1 D、a=1，b=0，c=﹣1

查看试题解析
4. 在平面直角坐标系中，将△AOB绕原点O顺时针旋转180°后得到△A₁OB₁ ，若点B的坐标为（2，1），则点B的对应点B₁的坐标为（）

A、（1，2） B、（2，－1） C、（－2，1） D、（－2，－1）

查看试题解析
5. 将抛物线 $y = x^{2}$ 向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的函数表达式为（）

A、 $y = {(x + 2)}^{2} - 3$ B、 $y = {(x + 2)}^{2} + 3$ C、 $y = {(x - 2)}^{2} + 3$ D、 $y = {(x - 2)}^{2} - 3$

查看试题解析
6. 方程 $x^{2} + 6 x - 5 = 0$ 的左边配成完全平方后所得方程为（）

A、 ${(x + 3)}^{2} = 14$ B、 ${(x - 3)}^{2} = 14$ C、 ${(x + 3)}^{2} = 4$ D、 ${(x - 3)}^{2} = 4$

查看试题解析
7. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分比率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）

A、 $560 {(1 + x)}^{2} = 315$ B、 $560 {(1 + 2 x)}^{2} = 315$ C、 $560 {(1 - 2 x)}^{2} = 315$ D、 $560 {(1 - x)}^{2} = 315$

查看试题解析
8. 已知1是关于x的一元二次方程（m﹣1）x²+x+1=0的一个根，则m的值是（　　）
　

A、1 B、﹣1 C、0 D、无法确定

查看试题解析
9. 若抛物线的顶点为点（2，3）且抛物线经过点（3，1），那么抛物线解析式是（）

A、y=4（x-2）² -3 B、y=-2（x-2）²+3 C、y=-2（x-2）²-3 D、y= - $\frac{2}{25}$ (x-2）²+3

查看试题解析
10. 如果关于 $x$ 的方程 $k x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则 $k$ 的取值范围是（）

A、 $k < 1$ B、 $k < 1$ 且 $k \neq 0$ C、 $k > 1$ D、 $k \leq 1$ 且 $k \neq 0$

查看试题解析
11. 若抛物线y＝x²＋mx的对称轴是x＝2.5，则关于x的方程x²＋mx＝6的解为（）.

A、－2，3 B、2，－3 C、－1，6 D、1，－6

查看试题解析
12. 二次函数y=ax²+bx+c的y与x的部分对应值如表，则下列判断中正确的是（）
x
…
0
1
3
4
…
y
…
2
4
2
-2
…

A、抛物线开口向上 B、y最大值为4 C、当x＞1时，y随着x的增大而减小 D、当0＜x＜2时，y＞2

查看试题解析

二、填空题

13. 如图，将 $△ A B C$ 绕点 $A$ 按顺时针方向旋转某个角度得到 $△ A B^{'} C^{'}$ ，使 $A B^{'} / / C B$ ， $C B$ ， $A C^{'}$ 的线相交于点 $D$ ，如果 $∠ D = 28 °$ ，那么 $∠ B A C =$ ．

查看试题解析
14. 一元二次方程 $(x + 6)^{2} = 5$ 可转化为两个一次方程，其中一个一次方程是 $x + 6 = \sqrt{5}$ ，则另一个一次方程是.

查看试题解析
15. 已知 $x_{1}, x_{2}$ 是一元二次方程 $x^{2} - 2 x - 1 = 0$ 的两根，则 $\frac{1}{x_{1} x_{2}} =$ .

查看试题解析
16. 二次函数 $y = a x^{2} + b x + c$ 的图象如图，则方程 $a x^{2} + b x + c = 0$ 的解为．

查看试题解析
17. 若 $y = (a + 2) x^{| a |} + 1$ 是以x为自变量的二次函数，则a= ．

查看试题解析
18. 如图是一张长 $20 c m$ 、宽 $12 c m$ 的矩形纸板．将纸板四个角各剪去一个边长为 $x c m$ 的正方形，然后将四周突出部分折起，可制成一个底面积是 $180 c m^{2}$ 的无盖长方体纸盒，则 $x$ 的值为．

查看试题解析
19. 抛物线的部分图像如图所示，则当y＞0时，x的取值范围是．

查看试题解析
20. 如图，铅球运动员掷铅球的高度 $y$ (m)与水平距离 $x$ (m)之间的函数关系式是： $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则该运动员此次掷铅球的成绩是 m.

查看试题解析

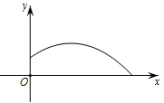
三、解答题

21. 在平面直角坐标系中， $Δ A B C$ 的位置如图所示（每个小方格都是边长为1个单位长度的正方形）.其中 $A (1 ， 1)$ 、 $B (4 ， 4)$ 、 $C (5 ， 1)$ .
⑴将 $Δ A B C$ 沿 $x$ 轴方向向左平移6个单位，画出平移后得到的 $Δ A_{1} B_{1} C_{1}$ ；
⑵将 $Δ A B C$ 绕着点 $A$ 顺时针旋转90°，画出旋转后得到的 $Δ A_{2} B_{2} C_{2}$ ， $A$ 、 $B$ 、 $C$ 的对应点 $C$ 分别是 $A_{2}$ 、 $B_{2}$ 、 $C_{2}$ ；

查看试题解析
22. 已知关于x的一元二次方程x²+2x﹣k＝0有两个不相等的实数根．

(1)、求k的取值范围；

(2)、当k＝1时，求方程的解．

查看试题解析
23. 如图， $Δ A B C$ 逆时针旋转一定角度后与 $Δ A D E$ 重合，且点C在AD上.

(1)、指出旋转中心；

(2)、若 $∠ B = 21^{°}$ ， $∠ A C B = 26^{°}$ ，求出旋转的度数；

(3)、若 $A B = 5$ ， $C D = 3$ ，则AE的长是多少？为什么？

查看试题解析
24. 从地面竖直向上抛出一个小球，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是 $h = 30 t - 5 t^{2}$ ．

(1)、小球从抛出到落地经过了多少秒？

(2)、当小球的运动时间是多少时，小球最高？小球运动中的最大高度是多少？

查看试题解析
25. 今年我国发生了较为严重的新冠肺炎疫情，口罩供不应求．某商店恰好年前新进了一批口罩，若按每个盈利1元销售，每天可售出200个，如果每个口罩的售价上涨0.5元，则销售量就减少10件，问应将每件涨价多少元时，才能让顾客得到实惠的同时每天利润为480元？

查看试题解析
26. 如图：已知抛物线的顶点为A（1，4），抛物线与y轴交于点B（0，3）与x轴交于C、D两点，点P是x轴上的一个动点.

(1)、求抛物线的解析式；

(2)、当PA+PB的值是最小时，求点P的坐标.

查看试题解析

x	…	0	1	3	4	…
y	…	2	4	2	-2	…