江西省上饶市余干县八校联考2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 二次函数y= $- \frac{1}{2}$ (x+1)²-3的对称轴为直线（）

A、x=3 B、x=-3 C、x=1 D、x=-1

查看试题解析
2. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若x₁、x₂是方程x²-2x-3=0的两根，则x₁+x₂+x₁x₂的值是（）

A、1 B、-1 C、5 D、-5

查看试题解析
4. 如图， $B C$ 是 $⊙ O$ 的直径， $A B$ 是 $⊙ O$ 的弦.若 $∠ A O C = 60 °$ ，则 $∠ O A B$ 的度数是（）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $35 °$

查看试题解析
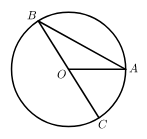5. 如图，在△ABC中，∠ACB＝90°，∠BAC＝20°，将△ABC绕点C顺时针旋转90°得到△A'B'C'，点B的对应点B'在边AC上（不与点A，C重合），则∠AA'B'的度数为（）

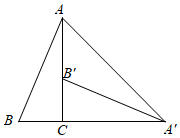A、20° B、25° C、30° D、45°

查看试题解析
6. 二次函数的 $y$ 与 $x$ 的部分对应值如表，则下列判断中正确的是（）

$x$

…

0

1

3

4

…

$y$

…

2

4

2

－2

…

A、抛物线开口向上 B、 $y$ 的最大值为4 C、当 $x > 1$ 时， $y$ 随 $x$ 的增大而减小 D、当 $0 < x < 2$ 时， $2 < y \leq \frac{17}{4}$

查看试题解析

二、填空题

7. 已知方程x²+x﹣k＝0有一根为﹣2，则该方程的另一个根为．

查看试题解析
8. 如图， $△$ ABC的三个顶点都在方格纸的格点上，其中A点的坐标是 $(- 1 ， 0)$ ，现将 $△$ ABC绕A点按逆时针方向旋转 $90 °$ ，则旋转后点C对应点的坐标是．

查看试题解析
9. 如图，AB是⊙O的直径，CD是⊙O的弦，连接AC、AD，若∠CAB＝35°，则∠ADC的度数为度．

查看试题解析
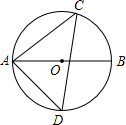10. 已知关于x的方程mx²﹣2x+1＝0有两个不相等的实数根，则m的取值范围是．

查看试题解析
11. 如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，AC＝3，将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′，使点C′落在AB边上，连接BB′，则BB′的长度为．

查看试题解析
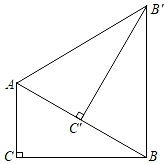12. 已知正方形ABCD中，AB＝2，⊙A是以A为圆心，1为半径的圆，若⊙A绕点B顺时针旋转，旋转角为α（0°＜α＜180°），则当旋转后的圆与正方形ABCD的边相切时，α＝．

查看试题解析

三、解答题

13.

(1)、解方程：5（x﹣2）²＝2（2﹣x）；

(2)、已知二次函数y＝kx²﹣2x+1的图象与x轴无交点，求k的取值范围．

查看试题解析
14. 如图，△ABC中，AD是中线，将△ABD旋转后与△ECD重合.

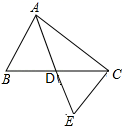(1)、旋转中心是点，旋转了度；

(2)、如果AB＝3，AC＝4，求中线AD长的取值范围.

查看试题解析
15. 如图，点A，B，C在⊙O上，且∠ABC＝120°，请仅用无刻度的直尺，按照下列要求作图．（保留作图痕迹，不写作法）

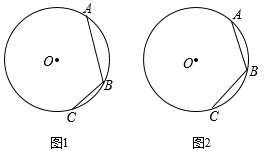(1)、在图（1）中，AB＞BC，作一个度数为30°的圆周角；

(2)、在图（2）中，AB＝BC，作一个顶点均在⊙O上的等边三角形．

查看试题解析
16. 已知抛物线 $y = a x^{2} + b x - 1$ 经过 $A (1 ， 2)$ ， $B (- 3 ， 2)$ 两点．

(1)、求该抛物线的函数关系式；

(2)、若将该抛物线向上平移3个单位长度，求出平移后的函数关系式并直接写出开口方向及顶点坐标．

查看试题解析
17. 某市新冠疫情防控应急指挥部要求全市18岁以上符合新冠疫苗接种的人群应打尽打，为落实这一要求，梅林区经统计7月份共有2500人接种，9月份增加到3600人，如果每月接种人数的增长率相同，求每月接种人数的平均增长率．

查看试题解析
18. 已知关于x的方程x²﹣2x+m＝0的一个根为1+ $\sqrt{2}$ ．

(1)、求m的值及方程的另一个根．

(2)、设方程的两个根为x₁ ， x₂ ，求式子x₁²⁰²⁰x₂²⁰²¹+x₁的值．

查看试题解析
19. 如图是某蔬菜基地搭建一座圆弧型蔬菜棚，跨度AB＝3.2米，拱高CD＝0.8米（C为AB的中点，D为弧AB的中点）．

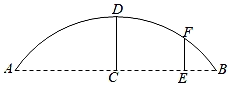(1)、求该圆弧所在圆的半径；

(2)、在距蔬菜棚的一端0.4米处竖立支撑杆EF，求支撑杆EF的高度．

查看试题解析
20. 直播购物逐渐走进了人们的生活，某电商在抖音上对一款成本价为8元的小商品进行直播销售，如果按每件10元销售，每天可卖出200件，通过市场调查发现，每件小商品售价每上涨1元，销售件数减少20件．

(1)、应将每件售价定为多少元时，才能使每天利润为640元？

(2)、电商想要获得每天800元的利润，小红同学认为不可能，那么你同意小红同学的说法吗？（说明理由）

查看试题解析
21. 如图，四边形ABCD内接于⊙O，AB为⊙O的直径，过点C作CE⊥AD交AD的延长线于点E，延长EC，AB交于点F，CD＝CB，连接AC．

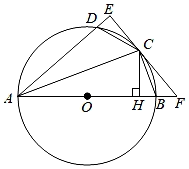(1)、求证：EF为⊙O的切线；

(2)、过点C作CH⊥AB，垂足为H，若DE＝1，CH＝3，求AC长．

查看试题解析
22. 如图，二次函数y＝ax²+bx﹣3（x≤3）的图象过点A（﹣1，0），B（3，0），C（0，c），记为L．将L沿直线x＝3翻折得到“部分抛物线”K，点A，C的对应点分别为点A'，C'．

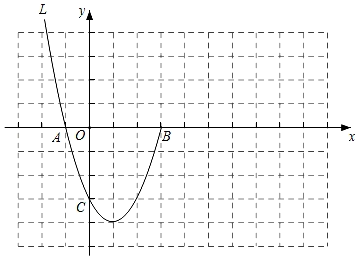(1)、求a，b，c的值；

(2)、在平面直角坐标系中描出点A'，C'，并画出“部分抛物线”K；

(3)、求“部分抛物线”K的解析式；

(4)、某同学把L和“部分抛物线”K看作一个整体，记为图形“W”，若直线y＝m和图形“W”只有两个交点M，N（点M在点N的左侧）．
①直接写出m的取值范围；
②若△MNB为等腰直角三角形，求m的值．

查看试题解析
23. 如图1，我们把一副两个三角板如图摆放在一起，其中OA，OD在一条直线上，∠B＝45°，∠C＝30°，固定三角板ODC，将三角板OAB绕点O按顺时针方向旋转，记旋转角∠AOA'＝α（0＜α＜180°）．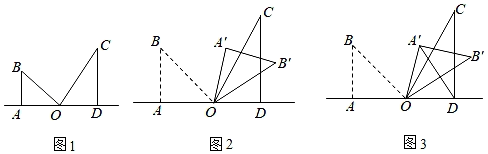

(1)、在旋转过程中，当α为度时，A'B' $∥$ OC，当α为度时，A'B'⊥CD；

(2)、如图2，将图1中的△OAB以点O为旋转中心旋转到△OA'B'的位置，求当α为多少度时，OB'平分∠COD；

(3)、当90°＜α＜120°时，连接A'D，利用图3探究∠B'A'D+∠B'OC+∠A'DC值的大小变化情况，并说明理由．

查看试题解析

$x$	…	0	1	3	4	…
$y$	…	2	4	2	－2	…