江西省南昌市南昌县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列4个图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程x²+kx－1＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
3. 在平面直角坐标系中，将二次函数 $y = x^{2}$ 的图像向左平移2个单位长度，再向上平移1个单位长度，所得抛物线对应的函数表达式为（）

A、 $y = {(x - 2)}^{2} + 1$ B、 $y = {(x + 2)}^{2} + 1$ C、 $y = {(x + 2)}^{2} - 1$ D、 $y = {(x - 2)}^{2} - 1$

查看试题解析
4. 某校八年级组织一次篮球赛，各班均组队参赛，赛制为单循环形式（每两班之间都赛一场），共需安排15场比赛，则八年级班级的个数为（）

A、5 B、6 C、7 D、8

查看试题解析
5. 如图，已如抛物线 $y = a x^{2} + b x + c$ 开口向上，与 $x$ 轴的一个交点为 $(- 1 ， 0)$ ，对称轴为直线 $x$ $= 1$ .下列结论错误的是（）

A、 $a b c > 0$ B、 $b^{2} > 4 a c$ C、 $4 a + 2 b + c > 0$ D、 $2 a + b = 0$

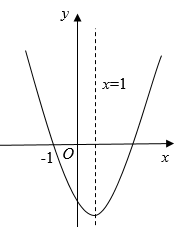查看试题解析
6. 如图，在平面直角坐标系中，以坐标原点O为顶点的正方形OBCD，其中点D（2，0），点B在y轴上，点C在第一象限，以BC为边在正方形OBCD外作等边△ABC，若将△ABC与正方形OBCD组成的图形绕点O顺时针旋转，每次旋转90°，则第2020次旋转结束时，点A的坐标为（）

A、（1，2+ $\sqrt{3}$ ） B、（2+ $\sqrt{3}$ ， ﹣1） C、（﹣1，﹣2﹣ $\sqrt{3}$ ） D、（﹣2﹣ $\sqrt{3}$ ， ﹣1）

查看试题解析

二、填空题

7. 若 $x_{1} ， x_{2}$ 是方程 $x^{2} + 3 x = 0$ 的两个根，则 $x_{1} + x_{2} =$ .

查看试题解析
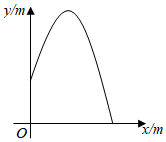
8. 已知点P（a﹣3，7）关于原点对称的点在第四象限，则a的取值范围是．

查看试题解析
9. 将y=-2(x-1)²+8的图象先向左平移2个单位，再向下平移5个单位，则最终所得图象的函数表达式为 .

查看试题解析
10. 从喷水池喷头喷出的水珠，在空中形成一条抛物线，如图所示，在抛物线各个位置上，水珠的竖直高度 $y$ （单位： $m$ ）与它距离喷头的水平距离 $x$ （单位： $m$ ）之间满足函数关系式 $y = - 2 x^{2} + 4 x + 1$ ，喷出水珠的最大高度是 $m$ .

查看试题解析
11. 如图，将边长为1的正方形 $A B C D$ 绕点 $A$ 顺时针旋转 $30 °$ 到 $A B_{1} C_{1} D_{1}$ 的位置，则阴影部分的面积是；

查看试题解析
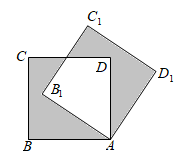12. 如图，已知二次函数 $y = a x^{2} + b x + c$ （a≠0（的图象，且关于x的一元二次方程 $a x^{2} + b x + c - m = 0$ 没有实数根，有下列结论：① $b^{2} - 4 a c > 0$ ；② $a b c < 0$ ；③ $m < - 3$ ；④ $3 a + b > 0$ .其中正确结论的序号有.

查看试题解析

三、解答题

13. 解方程：

(1)、4x²＝12x；

(2)、3x²﹣4x﹣2＝0.

查看试题解析
14. 已知函数 $y = (m - 3) {(x + 2)}^{m^{2} - 7} + m - 2$ 是二次函数．

(1)、求m的值；

(2)、求这个二次函数的解析式，并指出开口方向、对称轴和顶点坐标．

查看试题解析
15. 如图，在正方形网格中， $△ A B C$ 的顶点在格点上，请仅用无刻度直尺完成以下作图（保留作图痕迹）．

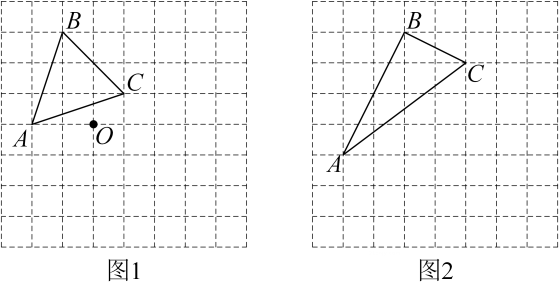(1)、在图1中，作 $△ A B C$ 关于点O对称的 $△ A^{'} B^{'} C^{'}$ ；

(2)、在图2中，作 $△ A B C$ 绕点A顺时针旋转一定角度后，顶点仍在格点上的 $△ A^{'} B^{'} C^{'}$ ．

查看试题解析
16. 已知二次函数的顶点坐标为 $A (1 ， - 4)$ ，且经过点 $B (3 ， 0)$ .

(1)、求该二次函数的解析式；

(2)、判断点 $C (2 ， - 3)$ 是否在该函数图象上，并说明理由.

查看试题解析
17. 2021年7日1日建党100周年纪念日，在本月日历表上可以用一个方框圈出4个数（如图所示），若圈出的四个数中，最小数与最大数的乘积为65，求这个最小数（请用方程知识解答）．

查看试题解析
18. 关于 $x$ 的一元二次方程 $x^{2} - (k + 3) x + 2 k + 2 = 0$ .

(1)、求证：方程总有两个实数根；

(2)、若方程有一根小于1，求 $k$ 的取值范围.

查看试题解析
19. 某超市经销一种商品，每件成本为50元.经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件.设该商品每件的销售价为x元，每个月的销售量为y件.

(1)、求y与x的函数表达式；

(2)、当该商品每件的销售价为多少元时，每个月的销售利润最大？最大利润是多少？

查看试题解析
20. 已知抛物线y＝-2x²+(m-3)x-8.

(1)、若抛物线的对称轴为y轴，求m的值；

(2)、若抛物线的顶点在x正半轴上，求m的值.

查看试题解析
21. 如图，点 $A ， B$ 在函数 $y = \frac{1}{4} x^{2}$ 的图像上．已知 $A ， B$ 的横坐标分别为－2、4，直线 $A B$ 与 $y$ 轴交于点 $C$ ，连接 $O A ， O B$ ．

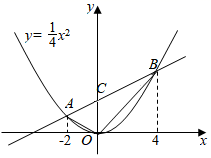(1)、求直线 $A B$ 的函数表达式；

(2)、求 $Δ A O B$ 的面积；

(3)、若函数 $y = \frac{1}{4} x^{2}$ 的图像上存在点 $P$ ，使得 $Δ P A B$ 的面积等于 $Δ A O B$ 的面积的一半，则这样的点 $P$ 共有个．

查看试题解析
22. 如图，在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF＝45°，求证：EF＝DF+BE．观察：EF，DF，BE三条线段都不在同一条直线上，能不能借助图形的运动，将部分线段放置在一条直线上加以证明呢？思路：将△ABE绕点A顺时针旋转9O°使AB与AD重合，得到了旋转后的△ADG．
①根据上述思路在图中画图分析并证明（写出详细的证明过程）．
②若正方形ABCD的边长为6，当动点E在BC边上运动到中点位置时，动点F在CD边上距离D点多长的位置？

查看试题解析
23. 甲秀楼是贵阳市一张靓丽的名片.如图①，甲秀楼的桥拱截面 $O B A$ 可视为抛物线的一部分，在某一时刻，桥拱内的水面宽 $O A = 8 m$ ，桥拱顶点 $B$ 到水面的距离是 $4m$ .

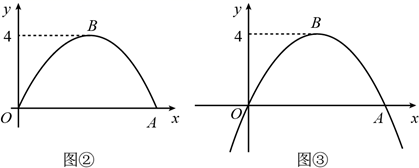(1)、按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；

(2)、一只宽为 $1 .2m$ 的打捞船径直向桥驶来，当船驶到桥拱下方且距 $O$ 点 $0 .4m$ 时，桥下水位刚好在 $O A$ 处.有一名身高 $1.68 m$ 的工人站立在打捞船正中间清理垃圾，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）；

(3)、如图③，桥拱所在的函数图象是抛物线 $y = a x^{2} + b x + c (a \neq 0)$ ，该抛物线在 $x$ 轴下方部分与桥拱 $O B A$ 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 $m (m > 0)$ 个单位长度，平移后的函数图象在 $8 \leq x \leq 9$ 时， $y$ 的值随 $x$ 值的增大而减小，结合函数图象，求 $m$ 的取值范围.

查看试题解析