江西省九江市湖口县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 矩形、菱形、正方形都具有的性质是（　　）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分对角

查看试题解析
2. 如果关于x的一元二次方程 $(m - 3) x^{2} + 3 x + m^{2} - 9 = 0$ ，有一个解是0，那么m的值是（）

A、3 B、-3 C、±3 D、0或-3

查看试题解析
3. 一个盒子内装有大小、形状相同的四个球，其中红球1个、绿球1个、白球2个，小明摸出一个球不放回，再摸出一个球，则两次都摸到白球的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{12}$

查看试题解析
4. 如图，已知△ABC∽△ADB，点D是AC的中点， AC=4 ，则AB的长为（）

A、2 B、4 C、 $2 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
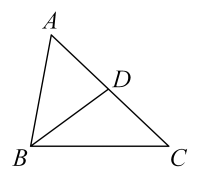5. 若m是方程 $x^{2} - x - 1 = 0$ 的根，则 $m^{3} - 2 m^{2}$ 的值为（）

A、-1 B、0 C、1 D、2

查看试题解析
6. 如图，以正方形 $A B C D$ 的顶点 $B$ 为直角顶点，作等腰直角三角形 $B E F$ ，连接 $A F$ 、 $F C$ ，当 $E$ 、 $F$ 、 $C$ 三点在--条直线上时，若 $B E = \sqrt{2}$ ， $A F = 3$ ，则正方形 $A B C D$ 的面积是（）

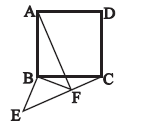A、10 B、14 C、5 D、7

查看试题解析

二、填空题

7. 若 $\frac{x}{y} = \frac{2}{3}$ ，则 $\frac{3 x + 2 y}{4 y + 3 x} =$ ．

查看试题解析
8. 有一只鸡患了 $H 7 N 9$ 流感，经过两轮传染后共有 $100$ 只鸡患了流感，那么每轮传染中，平均一只鸡传染的只数为．

查看试题解析
9. 现有4条线段，长度依次是2、4、6、7，从中任选三条，能组成三角形的概率是．

查看试题解析
10. 若 $x_{1}$ ， $x_{2}$ 是方程 $2 x^{2} - 3 x - 4 = 0$ 的两个根，则 $x_{1} x_{2} + x_{1} + x_{2}$ 的值为.

查看试题解析
11. 如图，在边长为6的正方形ABCD内作 $∠ E A F = 45 °$ ， AE交BC于点E，AF交CD于点F，连接EF，将 $△ A D F$ 绕点A顺时针旋转90°得到 $△ A B G$ ，若 $D F = 3$ ，则BE的长为．

查看试题解析
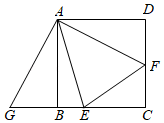12. 如图，在矩形ABCD中， $A B = 4$ ， $A D = 8$ ，点P在BC边上，点M在AD边上， $A M = 5$ ，点Q为AP的中点，当 $△ A M Q$ 为直角三角形时，AP的长为．

查看试题解析

三、解答题

13. 如图：

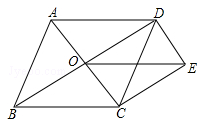(1)、解方程： $5 x^{2} - 8 x = - 2$

(2)、如图，点O是菱形ABCD对角线的交点， $D E ∥ A C$ ， $C E ∥ B D$ ，连接OE，求证： $O E = B C$ ．

查看试题解析
14. 印度古算书中有这样一首诗：“一群猴子分两队，高高兴兴在游戏．八分之一再平方，蹦蹦跳跳树林里；其余十二叽喳喳，伶俐活泼又调皮．告我总数共多少，两队猴子在一起．”你能解决这个问题吗？

查看试题解析
15. 如图，点E是正方形ABCD内一点，且 $E B = E C$ ，请仅用无刻度的直尺按要求作图（保留画图痕迹，不写作法）．

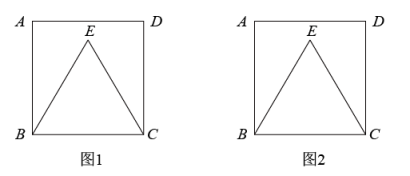(1)、在图1中，作出边BC的中点；

(2)、在图2中，作出边CD的中点．

查看试题解析
16. 小明从家到学校需要中途转车，从家到站台P有A、B、C三路车（乘A、B、C三路车的可能性相同）．到了站台P后转乘D路或E路到学校（乘D路、E路车的可能性相同）．

(1)、“小明从家到学校乘A路车”是事件；

(2)、请用列表或画树状图的方法，求小明乘坐A路、E路车到学校的概率．

查看试题解析
17. 如图，已知在△ABC中， AF⊥BC，CE⊥AB，垂足分别是F、E，求证：△BEF∽△BCA．

查看试题解析
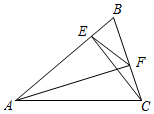18. 正方形ABCD的边长为6，点P在对角线BD上，点E是线段AD上或AD延长线上的一点，且 $P E ⊥ P C$ ．

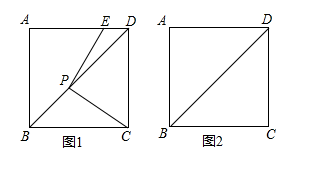(1)、如图1，点E在线段AD上，求证： $P E = P C$ ．

(2)、如图2，点E在线段AD的延长线上，请补全图形，并判断（1）中的结论是否仍然成立？请说明理由．

查看试题解析
19. 已知关于x的一元二次方程x²+(2m+1)x+m²−2=0．

(1)、若该方程有两个实数根，求m的最小整数值；

(2)、若方程的两个实数根为x₁ ， x₂ ，且 ${(x_{1} - x_{2})}^{2} + m^{2} = 21$ ，求m的值．

查看试题解析
20. 如图，在 $△ A B C$ 中，点D、E、F分别在AB、BC、AC边上， $D E ∥ A C$ ， $E F ∥ A B$ ．

(1)、求证： $△ B D E ∽ △ E F C$ ．

(2)、若 $B C = 12$ ， $\frac{A F}{F C} = \frac{1}{2}$ ，求线段BE的长．

查看试题解析
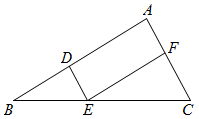21. 某商店将进价为8元的商品按每件10元售出，每天可售出200件，现在采取提高商品售价减少销售量的办法增加利润，如果这种商品每件的销售价每提高0.5元其销售量就减少10件，问：

(1)、应将每件售价定为多少元时，才能使每天利润为640元？

(2)、店主想要获得每天800元的利润，小红同学认为不可能，如果你同意小红同学的说法，请进行说明；如果你不同意，请简要说明理由．

查看试题解析
22. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．

(1)、求证：四边形OEFG是矩形；

(2)、若AD=10，EF=4，求OE和BG的长．

查看试题解析
23. 综合与实践
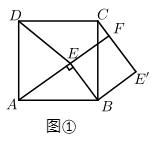
问题情境：
如图①，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′（点A的对应点为点C）．延长AE交CE′于点F，连接DE．
猜想证明：

(1)、试判断四边形BE'FE的形状，并说明理由；

(2)、如图②，若DA＝DE，请猜想线段CF与FE'的数量关系并加以证明；

(3)、如图①，若AB＝15，CF＝3，请求出DE的长．

查看试题解析