江西省景德镇市2020-2021学年九年级上学期期中数学试题

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程式属于一元二次方程的是（）

A、 $x^{2} - x^{3} - 7 = 0$ B、 $x^{2} - x = 2 + \frac{1}{x}$ C、 $(x + 1) (x - 1) = y$ D、 $x^{2} = 0$

查看试题解析
2. 在菱形ABCD中，周长为24，已知其两个相邻的内角度数比为 $1 ： 2$ ，则菱形ABCD中较短对角线长度为（）

A、6 B、8 C、 $6 \sqrt{3}$ D、 $8 \sqrt{3}$

查看试题解析
3. 随着10月18号第十七届景德镇国际博览会开幕，吸引来无数国内外陶瓷爱好者来景德镇旅游，外国友人汤姆和杰瑞计划看完陶瓷会展之后，然后各自在“古窑”，“瑶里”，“古县衙”，“陶溪川”这四个景点中选一个去参观，汤姆和杰瑞正好选中同一地方的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
4. 如图，E为 $▱ A B C D$ 的边CB的延长线上一点，若 $\frac{E B}{E C} = \frac{1}{3}$ ，则 $\frac{A F}{B F}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、2 D、3

查看试题解析
5. 已知3是关于x的方程 $x^{2} - a x + 2 a = 0$ 的一个根，并且这个方程的两个根恰好是等腰三角形ABC的两条边长，则三角形ABC的周长为（）

A、9 B、12 C、12或15 D、15

查看试题解析
6. 如图，在矩形ABCD中， $A D = 2$ ， $A B > 2$ ， AG平分 $∠ B A D$ ，分别过点B，C作 $B E ⊥ A G$ 于点E， $C F ⊥ A G$ 于点F，则 $A E - G F$ 的值为（）

A、1 B、2 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析

二、填空题

7. 已知m是方程 $x^{2} - x - 3 = 0$ 的一个根，则 $m^{2} - m =$ ．

查看试题解析
8. 如图，在正方形ABCD中，点E为边长AB延长线上一点，且 $A C = A E$ ，则 $∠ B C E =$ ．

查看试题解析
9. 在 $▱ A B C D$ 中，现有以下四个条件：① $A C = B D$ ， ② $A C ⊥ B D$ ， ③ $∠ A B C = 90 °$ ， ④ $A B = B C$ ，小马准备从以上四个条件中，随机选出两个，可以得出 $▱ A B C D$ 为正方形的概率为．

查看试题解析
10. 我国古代数学著作《九章算术》中记载了一个问题：“今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问：邑方几何？”．其大意是：如图，一座正方形城池，A为北门中点，从点A往正北方向走30步到B处有一树木，C为西门中点，从点C往正西方向走750步到D处正好看到B处的树木，则正方形城池的边长为步．

查看试题解析
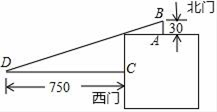11. 如图，在Rt△ABC中，∠ACB＝90°，AC＝5，BC＝12，D是AB上一动点，过点D作DE⊥AC于点E，DF⊥BC于点F，连接EF，则线段EF的最小值是．

查看试题解析
12. 如图，在直角梯形ABCD中， $A D ∥ B C$ ， $∠ D A B = 90 °$ ， $A B = 14$ ， $A D = 4$ ， $B C = 6$ ，动点P从点A出发，以每秒2个单位的速度向点B运动，运动到B点停止，若以点P，A，D为顶点的三角形与 $△ P B C$ 相似时，运动时间 $t =$ ．

查看试题解析

三、解答题

13.

(1)、解方程； $x^{2} - 4 x = - 1$ ．

(2)、已知 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4} \neq 0$ ，试求出 $\frac{2 x + 3 y - z}{z}$ 的值．

查看试题解析
14. 如图，在 $▱ A B C D$ 中，对角线AC与BD交于点O， $O H ⊥ A B$ 于点H，且 $A H = B H$ ，求证： $▱ A B C D$ 是矩形．

查看试题解析
15. 如图，AE为菱形ABCD的高，请用无刻度的直尺按要求画图（保留画图痕迹）．

(1)、在图1中，过点C画出AB边上的高CF；

(2)、在图2中，过点C画出AD边上的高CH．

查看试题解析
16. 李老师通过学习强国平台中的任务选项去获得每日积分，平台中获得每日积分的选项中大致可以分为以下几项：1.有效阅读；2.试听学习；3.每日答题；4.分享；5.强国运动（每项任务只能完成一次）．

(1)、李老师随机在以上5项任务中选择一项去完成，积分不少于5分的概率是多少？

(2)、李老师随机在以上5项任务中选择两项去完成，积分大于10分的概率是多少？（用树状图或者表格法表示）

查看试题解析
17. 已知关于x的方程 $x^{2} - (2 a + 1) x + a^{2} + 2 a - 3 = 0$ ．

(1)、若该方程有两个不相等的实数根，求实数α的取值范围；

(2)、若该方程的一个根为1时，求a的值．

查看试题解析
18. 在菱形ABCD中， $A B = 6$ ， $∠ B = 60 °$ ， E，F分别是BC，CD边上的两个动点，且 $B E = C F$ ．

(1)、证明： $A E = A F$ ；

(2)、点E，F在移动过程中， $△ A E F$ 的周长是否存在最小值，若存在，求出最小值，若不存在，请说明理由．

查看试题解析
19. 从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交．顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们就把这条线段叫做这个三角形的理想分割线．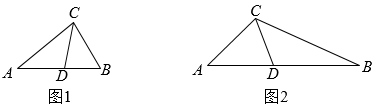

(1)、如图1，在 $△ A B C$ 中，CD为角平分线， $∠ A = 40 °$ ， $∠ B = 60 °$ ，求证：CD为 $△ A B C$ 的理想分割线；

(2)、如图2，在 $△ A B C$ 中，CD为 $△ A B C$ 的理想分割线，且 $△ A C D$ 是以CD为底的等腰三角形．
①若 $∠ A = 44 °$ ，求∠ACB的度数；
②若 $A C = 2$ ， $B C = \sqrt{2}$ ，求理想分割线CD的长．

查看试题解析
20. 由于新冠疫情的影响，口罩需求量急剧上升，经过连续两次价格的上调，口罩的价格由每包10元涨到了每包14.4元，

(1)、求出这两次价格上调的平均增长率；

(2)、在有关部门调控下，口罩价格还是降到了每包10元，而且调查发现，定价为每包10元时，一天可以卖出30包，每降价1元，可以多卖出5包，当销售额为315元时，且让顾客获得更大的优惠，应该降价多少元？

查看试题解析
21. 如图1，在正方形ABCD中， $A D = 12$ cm，动点M，N同时分别从A，C两点出发，均以1cm/s的速度做直线运动，已知点M沿射线AB运动，点N沿边BC的延长线运动，MN与直线AC相交于点E，设点M的运动时间为 $t (s)$ ， $△ M C N$ 的面积为 $S (c m^{2})$ ．

(1)、求S与t的函数关系式；

(2)、当M运动几秒时， $S_{△ M C N} = S_{△ A B C}$ ？

(3)、如图2，作 $M F ⊥ A C$ 于点F，点M在AB边上运动时，线段EF的长度是否会发生改变，不变，请求出EF的长度，如果改变，请说明理由．

查看试题解析
22. 如图，点E是正方形ABCD的边AB上一动点，点A与点F关于DE对称，点F在正方形ABCD的内部，作射线CF交DE延长线于点P，连接AP，EF，DF．

(1)、若 $∠ A D E = 20 °$ ，求∠DPC的度数；

(2)、试探究点E在边AB的任意位置时，AP与PC的位置关系，并说明理由；

(3)、若 $A B = 4$ ，直接写出BF的最小值．

查看试题解析
23. 定义：
如图1，关于直线PQ同侧有两点M，N，点T在直线PQ上，若 $∠ M T P = ∠ N T Q$ ，则称点M，N为关于直线PQ在T处的反射点．

(1)、理解：
如图2，在 $△ A B C$ 中，P，Q分别是AB，AC上的点， $C P = C B$ ， $P Q ∥ B C$ ．求证：C，Q为关于直线AB在P处的反射点．

(2)、应用：
如图3，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， D，E分别是AB，AC上的中点，且点C，E是关于直线AB在D处的反射点，求∠B的度数．

(3)、拓展：
如图4，BD是矩形ABCD的对角线，E是边BC延长线上一点，且 $C E = C B$ ，连接AE交CD于点F，交BD于点P，连接BF，CP．
①求证：点A，B为关于直线CD在F处的反射点；
②若点C，F为关于直线BD在P处的反射点， $C P = 2 P F = \sqrt{15}$ ，求AB的长．

查看试题解析