河北省唐山市玉田县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-22 类型:期中考试
一、单选题
-
1. 若关于的方程是一元二次方程,则的值不可能是( )A、1 B、-1 C、0 D、32. 已知 , , 是 , 的比例中项,那么为( )A、10 B、9 C、-9 D、±93. 2022年将在北京--张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示,选手成绩更稳定的是( )
 A、甲 B、乙 C、都一样 D、不能确定4. 老师出示问题:“解方程”,四位同学给出了以下答案:小琪:;子航:;一帆:;萱萱:其中答案正确的是( )A、小琪 B、子航 C、一帆 D、萱萱5. 如图所示,已知 , 那么下列结论正确的是( )
A、甲 B、乙 C、都一样 D、不能确定4. 老师出示问题:“解方程”,四位同学给出了以下答案:小琪:;子航:;一帆:;萱萱:其中答案正确的是( )A、小琪 B、子航 C、一帆 D、萱萱5. 如图所示,已知 , 那么下列结论正确的是( )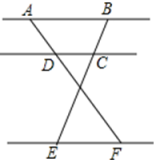 A、 B、 C、 D、6. 下列关于的一元二次方程中,两根之和为5的是( )A、 B、 C、 D、7. 某校在计算学生的数学总评成绩时,规定期中考试成绩占40%,期末考试成绩占60%,林琳同学的期中数学考试成绩为分,期末数学考试成绩为94分,那么他的数学总评成绩是( )A、86分 B、88分 C、90分 D、90.8分8. 如图,平行四边形 的对角线 , 相交于点O,E是 的中点,则 与 的面积的比等于( )
A、 B、 C、 D、6. 下列关于的一元二次方程中,两根之和为5的是( )A、 B、 C、 D、7. 某校在计算学生的数学总评成绩时,规定期中考试成绩占40%,期末考试成绩占60%,林琳同学的期中数学考试成绩为分,期末数学考试成绩为94分,那么他的数学总评成绩是( )A、86分 B、88分 C、90分 D、90.8分8. 如图,平行四边形 的对角线 , 相交于点O,E是 的中点,则 与 的面积的比等于( )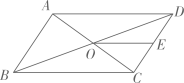 A、 B、 C、 D、9. 如图,点为边上的任意一点,作于点 , 于点 , 下列用线段比表示的值,正确的是( )
A、 B、 C、 D、9. 如图,点为边上的任意一点,作于点 , 于点 , 下列用线段比表示的值,正确的是( )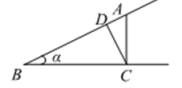 A、 B、 C、 D、10. 扬帆中学有一块长 ,宽 的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为 ,则可列方程为( )
A、 B、 C、 D、10. 扬帆中学有一块长 ,宽 的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为 ,则可列方程为( )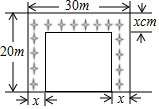 A、 B、 C、 D、11. 班长王亮依据今年月“书香校园”活动中全班同学的课外阅读数量单位:本 , 绘制了如图折线统计图,下列说法正确的是( )
A、 B、 C、 D、11. 班长王亮依据今年月“书香校园”活动中全班同学的课外阅读数量单位:本 , 绘制了如图折线统计图,下列说法正确的是( ) A、每月阅读数量的平均数是58 B、众数是83 C、中位数是50 D、每月阅读数量超过50的有5个月12. 如图,琪琪一家驾车从地出发,沿着北偏东的方向行驶,到达地后沿着南偏东的方向行驶来到地,且地恰好位于地正东方向上,则下列说法正确的是( )
A、每月阅读数量的平均数是58 B、众数是83 C、中位数是50 D、每月阅读数量超过50的有5个月12. 如图,琪琪一家驾车从地出发,沿着北偏东的方向行驶,到达地后沿着南偏东的方向行驶来到地,且地恰好位于地正东方向上,则下列说法正确的是( )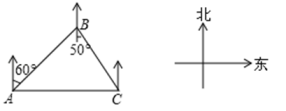 A、地在地的北偏西方向上 B、地在地的南偏西方向上 C、 D、13. 如图,原点在网格格点上的平面直角坐标系中,两个三角形(顶点均在网格的格点上)是以点 为位似中心的位似图形,则点 的坐标是( )
A、地在地的北偏西方向上 B、地在地的南偏西方向上 C、 D、13. 如图,原点在网格格点上的平面直角坐标系中,两个三角形(顶点均在网格的格点上)是以点 为位似中心的位似图形,则点 的坐标是( ) A、 B、 C、 D、14. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( )
A、 B、 C、 D、14. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( ) A、①处 B、②处 C、③处 D、④处15. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A、①处 B、②处 C、③处 D、④处15. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )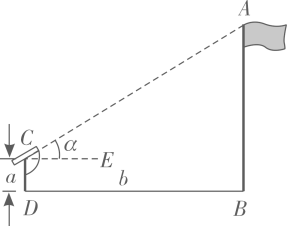 A、 B、 C、 D、16. 如图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面直径AB的长度是( )
A、 B、 C、 D、16. 如图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面直径AB的长度是( ) A、2cm B、2.5cm C、3cm D、4cm
A、2cm B、2.5cm C、3cm D、4cm二、填空题
-
17. 已知一组数据1,2,3,它们的平均数是2,则 , 这一组数据的方差为 .18. 小刚在解关于的方程时,只抄对了 , , 解出其中一个根是他核对时发现所抄的比原方程的值小2则 , 原方程的根的情况是 .19. 如图,在正方形中,是边的中点,是边上异于 , 的一点.
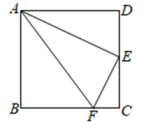 (1)、若∽ , 则;(2)、当与满足数量关系时,∽ .
(1)、若∽ , 则;(2)、当与满足数量关系时,∽ .三、解答题
-
20. 如图,在中,于点 , 若 , , .
 (1)、求边的长;(2)、求的值.21. 如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
(1)、求边的长;(2)、求的值.21. 如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.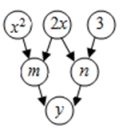 (1)、当时,请直接写出的值;(2)、当时,求的值.22. 如图,嘉琪在一座桥的附近试飞一架小型无人机,无人机飞行的高度为AD,且D,B,C在同一水平线上.
(1)、当时,请直接写出的值;(2)、当时,求的值.22. 如图,嘉琪在一座桥的附近试飞一架小型无人机,无人机飞行的高度为AD,且D,B,C在同一水平线上.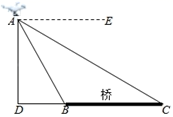 (1)、有下列说法:①无人机俯视桥头B的俯角为∠EAC;②无人机俯视桥头C的俯角为∠C;③站在桥头B处看无人机的仰角为∠ABD;④从C处走向B处的过程中观察无人机,仰角越来越大;其中正确的是(只填序号即可).(2)、若∠EAB=60°,∠EAC=30°,桥BC的长度为24米,求无人机飞行的高度AD(结果保留整数,参考数据 , ).23. 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,:4棵;:5棵;:6棵;:7棵.将各类的人数绘制成扇形统计图和条形统计图(如图所示),经确认扇形统计图是正确的,而条形统计图尚有一处不符合题意.
(1)、有下列说法:①无人机俯视桥头B的俯角为∠EAC;②无人机俯视桥头C的俯角为∠C;③站在桥头B处看无人机的仰角为∠ABD;④从C处走向B处的过程中观察无人机,仰角越来越大;其中正确的是(只填序号即可).(2)、若∠EAB=60°,∠EAC=30°,桥BC的长度为24米,求无人机飞行的高度AD(结果保留整数,参考数据 , ).23. 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,:4棵;:5棵;:6棵;:7棵.将各类的人数绘制成扇形统计图和条形统计图(如图所示),经确认扇形统计图是正确的,而条形统计图尚有一处不符合题意.
回答下列问题:
(1)、写出条形统计图中存在的不符合题意,并说明理由;(2)、写出这20名学生每人植树量的众数、中位数;(3)、在求这20名学生每人植树量的平均数时,小宇是这样分析的:第一步:求平均数的公式是;
第二步:在该问题中, , , , , ;
第三步:(棵).
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估这260名学生共植树多少棵.
24. 卫生部疾病控制专家经过调研提出,如果1人传播10人以上而且被传染的人已经确定为新冠肺炎,那么这个传播者就可以称为“超级传播者”如果某镇有1人不幸成为新冠肺炎病毒的携带者,假设每轮传染的人数相同,经过两轮传染后共有144人成为新冠肺炎病毒的携带者.(1)、经过计算,判断最初的这名病毒携带者是“超级传播者”吗?请先写出结论,再说明理由;(2)、若不加以控制传染渠道,经过3轮传染,共有多少人成为新冠肺炎病毒的携带者?25. 如图,在矩形中, , , 点在边上, , 点从点出发沿折线匀速移动,到达点时停止. (1)、边AD的长为;(2)、设点运动的时间为秒,若点从到再到共用时28秒.连接 , 请求出当被线段截得的三角形与相似时的值.
(1)、边AD的长为;(2)、设点运动的时间为秒,若点从到再到共用时28秒.连接 , 请求出当被线段截得的三角形与相似时的值.