山东省淄博市高青县2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-09-22 类型:期中考试
一、单选题
-
1. 下列四个图形中,轴对称图形有( )个.
 A、1 B、2 C、3 D、42. 三角形三边之长分别是:①3,4,5;②8,15,17;③9,24,25;④13,12,15.其中能构成直角三角形的有( )A、1个 B、2个 C、3个 D、4个3. 如图,已知△ABC≌△CDE,其中AB=CD,错误的是( )
A、1 B、2 C、3 D、42. 三角形三边之长分别是:①3,4,5;②8,15,17;③9,24,25;④13,12,15.其中能构成直角三角形的有( )A、1个 B、2个 C、3个 D、4个3. 如图,已知△ABC≌△CDE,其中AB=CD,错误的是( ) A、AC=CE B、∠BAC=∠DCE C、∠ACB=∠ECD D、∠B=∠D4. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB , 若CD=10,则点D到AB的距离是( )
A、AC=CE B、∠BAC=∠DCE C、∠ACB=∠ECD D、∠B=∠D4. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB , 若CD=10,则点D到AB的距离是( )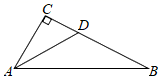 A、8 B、9 C、10 D、115. 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )
A、8 B、9 C、10 D、115. 如图,AB=AC,若要使△ABE≌△ACD,则添加的一个条件不能是( )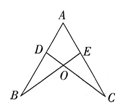 A、∠B=∠C B、BE=CD C、BD=CE D、∠ADC=∠AEB6. 下列各图中,作△ABC边AC上的高,正确的是( )A、
A、∠B=∠C B、BE=CD C、BD=CE D、∠ADC=∠AEB6. 下列各图中,作△ABC边AC上的高,正确的是( )A、 B、
B、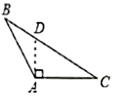 C、
C、 D、
D、 7. 已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )A、等边三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形8. 在等腰三角形ABC中,∠A=2∠B,则∠C的度数为( )A、36° B、45° C、36°或45° D、45°或72°9. 下列说法正确的是( )
7. 已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )A、等边三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形8. 在等腰三角形ABC中,∠A=2∠B,则∠C的度数为( )A、36° B、45° C、36°或45° D、45°或72°9. 下列说法正确的是( )①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;
④三角形的三条高都在三角形内部.
A、①② B、②③ C、③④ D、②④10. 等腰三角形的一边长为5cm,另一边长为10cm,则该等腰三角形的周长为( )A、25cm B、15cm或25cm C、20cm D、20cm或25cm11. 图,等边中,于点分别为上的两个定点且 , 在上有一动点使最短,则的最小值为( ) A、 B、 C、 D、12. 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 , P2 , 连接P1P2交OA于M,交OB于N,若∠AOB=40°,则∠MPN的度数是( )
A、 B、 C、 D、12. 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 , P2 , 连接P1P2交OA于M,交OB于N,若∠AOB=40°,则∠MPN的度数是( ) A、90° B、100° C、120° D、140°
A、90° B、100° C、120° D、140°二、填空题
-
13. 如图,在△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 .
 14. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若△ABC的周长26cm,△AEC的周长17cm,则AB的长为 .
14. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若△ABC的周长26cm,△AEC的周长17cm,则AB的长为 . 15. 如图,已知△ABC的面积为10 , AD平分∠BAC且AD⊥BD于点D,则△ADC的面积为 .
15. 如图,已知△ABC的面积为10 , AD平分∠BAC且AD⊥BD于点D,则△ADC的面积为 . 16. 如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是cm.
16. 如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是cm. 17. 在 中, , , ,如果点P在AC边上,且点P到 的两个顶点的距离相等,那么AP的长为.
17. 在 中, , , ,如果点P在AC边上,且点P到 的两个顶点的距离相等,那么AP的长为.三、解答题
-
18. 如图,∠A=∠BCD,CA=CD,点E在BC上,且DE∥AB,求证:AB=EC.
 19. 如图,在△ABC中,AE是角平分线,AD是高,∠BAC=70°,∠EAD=10°,求∠B的度数.
19. 如图,在△ABC中,AE是角平分线,AD是高,∠BAC=70°,∠EAD=10°,求∠B的度数. 20. 如图,方格纸中每个小方格都是边长为1个单位的正方形,已知△ABC的三个顶点在格点上.
20. 如图,方格纸中每个小方格都是边长为1个单位的正方形,已知△ABC的三个顶点在格点上. (1)、画出△A1B1C1 , 使它与△ABC关于直线a对称;(2)、求出△A1B1C1的面积;(3)、在直线a上画出点P,使PA+PC最小,最小值为 ▲ .21. 如图,在三角形ABC中,AB=10,BC=12,AD为BC边上的中线,且AD=8,过点D作DE⊥AC于点E.
(1)、画出△A1B1C1 , 使它与△ABC关于直线a对称;(2)、求出△A1B1C1的面积;(3)、在直线a上画出点P,使PA+PC最小,最小值为 ▲ .21. 如图,在三角形ABC中,AB=10,BC=12,AD为BC边上的中线,且AD=8,过点D作DE⊥AC于点E. (1)、求证:AD⊥BC;(2)、求DE的长.22. 在等边△ABC中,D为AC的中点,延长BC至点E,使CE=DC,连接ED并延长交AB于点F.
(1)、求证:AD⊥BC;(2)、求DE的长.22. 在等边△ABC中,D为AC的中点,延长BC至点E,使CE=DC,连接ED并延长交AB于点F. (1)、求证:△DBE是等腰三角形;(2)、DF与DE有怎样的数量关系?请说明理由.
(1)、求证:△DBE是等腰三角形;(2)、DF与DE有怎样的数量关系?请说明理由.

