山东省烟台市牟平区(五四制)2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-09-22 类型:期中考试
一、单选题
-
1. 改革开放以来,我国众多科技实体在各自行业取得了举世瞩目的成就,大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表.上述四个企业的标志是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若长度分别为a,4,7的三条线段能组成一个三角形,则a的值可以是( )A、2 B、3 C、4 D、113. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、
2. 若长度分别为a,4,7的三条线段能组成一个三角形,则a的值可以是( )A、2 B、3 C、4 D、113. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、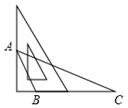 B、
B、 C、
C、 D、
D、 4. 如图,要使 , 下面给出的四组条件,错误的一组是( )
4. 如图,要使 , 下面给出的四组条件,错误的一组是( )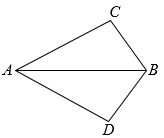 A、 , B、 , C、 , D、 ,5. 如图,在中, , , 与关于直线为称, , 连接 , 则的度数是( )
A、 , B、 , C、 , D、 ,5. 如图,在中, , , 与关于直线为称, , 连接 , 则的度数是( )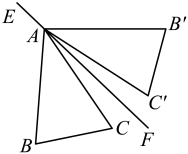 A、36° B、40° C、42° D、46°6. 如图,分别以线段AB的两端点A,B为圆心,大于 AB长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与O重合),连接PA,PB,则下列结论不一定成立的是( )
A、36° B、40° C、42° D、46°6. 如图,分别以线段AB的两端点A,B为圆心,大于 AB长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与O重合),连接PA,PB,则下列结论不一定成立的是( )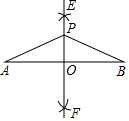 A、 B、 C、 D、7. 如图,是的边的垂直平分线,为垂足,交于点 , 且 , , , 则的周长是( )
A、 B、 C、 D、7. 如图,是的边的垂直平分线,为垂足,交于点 , 且 , , , 则的周长是( )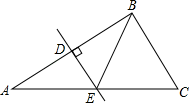 A、14 B、16 C、18 D、228. 勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )A、
A、14 B、16 C、18 D、228. 勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )A、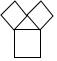 B、
B、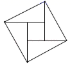 C、
C、 D、
D、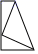 9. 下列说法:①满足的 , , 三条线段一定能组成三角形;②三角形的外心在三角形外部;③成轴对称的两个三角形一定全等;④在中,已知两边长分别为5和12,则第三边长为13;⑤在中,三边分别为 , , , 若 , 那么 , 其中正确的个数是( )A、4个 B、3个 C、2个 D、1个10.
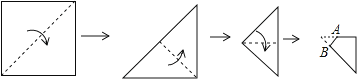
9. 下列说法:①满足的 , , 三条线段一定能组成三角形;②三角形的外心在三角形外部;③成轴对称的两个三角形一定全等;④在中,已知两边长分别为5和12,则第三边长为13;⑤在中,三边分别为 , , , 若 , 那么 , 其中正确的个数是( )A、4个 B、3个 C、2个 D、1个10.如图所示,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是( )
 A、
A、 B、
B、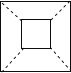 C、
C、 D、
D、 11. 如图,已知在四边形中, , 平分 , , , , 则四边形的面积是( )
11. 如图,已知在四边形中, , 平分 , , , , 则四边形的面积是( ) A、40 B、42 C、46 D、4812. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、40 B、42 C、46 D、4812. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
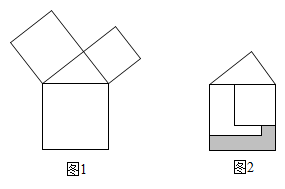 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和二、填空题
-
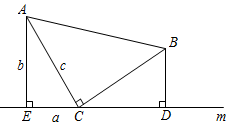
13. 正六边形对称轴的条数是条.14. 等腰三角形的两边长分别为7cm,15cm,其周长为cm.15. 在中,若一个内角等于另外两个内角的差,则最大一个内角等于 .16. 下面三个命题: 底边和顶角对应相等的两个等腰三角形全等; 两边及其中一边上的中线对应相等的两个三角形全等; 斜边和斜边上的中线对应相等的两个直角三角形全等,其中正确的命题的序号为 .17. 如图,已知 ,请你添加一个条件,使得 ,你添加的条件是 . (不添加任何字母和辅助线)
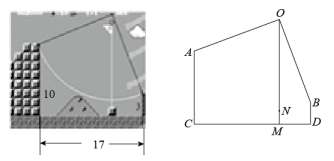
 18. 如图,长方体的长,宽,高分别是6,3,5,现一只蚂蚁从点爬行到点,设爬行的最短路线长为 , 则的值是 .
18. 如图,长方体的长,宽,高分别是6,3,5,现一只蚂蚁从点爬行到点,设爬行的最短路线长为 , 则的值是 .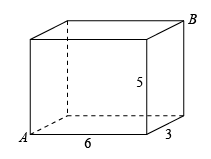
三、解答题
-
19. 把下列各数分别填入相应的集合内:
, -2,-3.14,0, , , -0.1212212221…,(每两个1之间依次增加1个2) , 0.232323……
(1)、有理数集合:{ …}.(2)、无理数集合:{ …}.(3)、请你再举出3个无理数的例子.20. 计算:(1)、求的算术平方根.(2)、求下列式子中的值: .21. 与关于直线成轴对称,如图所示: (1)、请用无刻度的直尺,在图1中作出对称轴所在直线 .(2)、类比图1的思维方式,请用无刻度的直尺,在图2中作出对称轴所在直线 .22. 如图,是上一点,交于点 , , , 求证: .
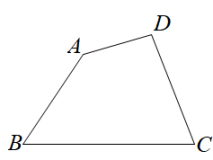
(1)、请用无刻度的直尺,在图1中作出对称轴所在直线 .(2)、类比图1的思维方式,请用无刻度的直尺,在图2中作出对称轴所在直线 .22. 如图,是上一点,交于点 , , , 求证: . 23. 已知:四边形 .
23. 已知:四边形 .求作:点 , 使 , 且点到边和的距离相等.(写出作图的方法,不必写具体步骤,保留作图痕迹)
 24. 如图, ,点 在 上.
24. 如图, ,点 在 上.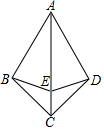 (1)、求证: 平分 ;(2)、求证: .25. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)、求证: 平分 ;(2)、求证: .25. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.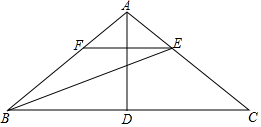 (1)、若∠C=36°,求∠BAD的度数;(2)、求证:FB=FE.
(1)、若∠C=36°,求∠BAD的度数;(2)、求证:FB=FE.