山东省威海市文登区2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 在 $△ A B C$ 中， $∠ A = 3 0^{∘}$ ， $∠ B = 5 0^{∘}$ ，那么 $△ A B C$ 形状是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
2. 下列学习用具中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依次为2，3，4，6，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任两螺丝之间距离最大为（）

A、10 B、8 C、7 D、5

查看试题解析
4. $△ A B C$ 是等腰三角形，若 $∠ A = 7 0^{∘}$ ，则 $∠ B$ 不可能是（）

A、40° B、50° C、55° D、70°

查看试题解析
5. 如图，已知AC垂直平分BD，垂足为E，下列结论不一定成立的是（）

A、 $A B = A D$ ． B、AC平分 $∠ B C D$ ． C、 $∠ A B C = ∠ A D C$ ． D、 $∠ B A D = ∠ B C D$ ．

查看试题解析
6. 如图，在 $△ A B C$ 中，AD是BC边上的高，BE平分 $∠ A B C$ 交AC边于E， $∠ B A C = 6 0^{∘}$ ， $∠ A B E = 2 5^{∘}$ ，则 $∠ D A C$ 的大小是（）

A、20° B、25° C、30° D、35.

查看试题解析
7. 如图，长方形门框高为2m，宽为1.5m，现有3块木板，尺寸如下：①号木板长3m，宽2.7m；②号木板长4m，宽2.4m；③号木板长2.8m，宽2.6m．能从这扇门通过的木板是（）

A、① B、② C、③号 D、都不能通过

查看试题解析
8. 如图，已知 $A E ∥ B F$ ， $A E = B F$ ，再添加下列一个条件，不能确定 $△ A C E ≌ △ B D F$ 的是（）

A、 $A D = B C$ B、 $∠ E = ∠ F$ C、 $E C = D F$ D、 $E C ∥ D F$

查看试题解析
9. 如图，已知 $A B = A C$ ， $∠ B = ∠ C$ ， $∠ 1 = ∠ 2$ ，给出下列结论：① $A E = A F$ ；② $A M = A N$ ；③ $B M = C N$ ；④ $D M = D N$ ．正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P，作射线AP交BC于点D，则下列说法中正确的个数是（）
①AD是∠BAC的平分线；②AD=BD；③AD=2CD；④S_△ABD=2 S_△ACD．

A、4个 B、3个 C、2个 D、1个

查看试题解析
11. 如图是由4个全等的直角三角形与1个小正方形拼成的正方形图案．已知大正方形面积为25，小正方形面积为1，若用a、b表示直角三角形的两直角边（a＞b），则下列说法：①a²+b²=25，②a－b=1，③ab=12，④a+b=7．正确的是（）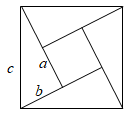

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析
12. 如图，是可调躺椅示意图，AE与BD的交点为C，且 $∠ A$ ， $∠ B$ ， $∠ E$ 保持不变．为了舒适，需调整 $∠ D$ 的大小，使 $∠ E F D = 11 0^{∘}$ ．根据图中数据信息，下列调整 $∠ D$ 大小的方法正确的是（）

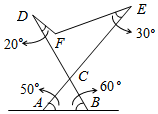A、增大10° B、减小10° C、增大15° D、减小15°

查看试题解析

二、填空题

13. 如图， $△ A B C ≌ △ D C B$ ，若 $∠ A = 8 0^{∘}$ ， $∠ D B C = 3 5^{∘}$ ，则 $∠ A C D$ 等于．

查看试题解析
14. 如图，两个正方形的面积分别是64和49，则AC的长为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A = 9 0^{∘}$ ， $A B = A C$ ， CD平分 $∠ A C B$ ， $D E ⊥ B C$ 于E，若 $A C = a$ ， $A D = b$ ，则 $△ D E B$ 的周长为．

查看试题解析
16. 如图所示，是一个外轮廓为矩形的机器零件平面示意图，根据图中标出尺寸（单位： $m m$ ）计算两圆孔中心A和B的距离为．

查看试题解析
17. $△ A B C$ 中， $A B = A C$ ， DE垂直平分AB，交BC与D，交AB与E， $A C = D C$ ．则 $∠ B A C$ 的大小为．

查看试题解析
18. 如图，长方体鱼缸长宽高分别为120cm，50cm，40cm，一只壁虎从外表面点A出发，沿长方体表面爬到内侧点E处，点E在棱 $D D^{'}$ 上且距离上沿10cm，壁虎爬行最短路程是cm．

查看试题解析

三、解答题

19. 已知：如图，△ABC中，∠BAC＝80°，AD⊥BC于D，AE平分∠DAC，∠B＝60°，求∠AEC的度数．

查看试题解析
20. 如图，∠C=90°，AC=12，BC=9，AD=8，BD=17，求△ABD的面积．

查看试题解析
21. 如图，已知△ABC中，∠B=2∠A，点D在边AC上，且CD＝CB．

(1)、用尺规作图：在AB边上求作一点P ，使点P到CA，CB距离相等（保留作图痕迹，不要求写作法）；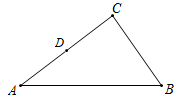

(2)、在（1）中，线段BP与AD是否相等？说明理由．

查看试题解析
22. 已知，如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，点D在AB边上．

(1)、图中哪一对三角形全等？说明理由；

(2)、若BD=9，AD=12，求DE的长．

查看试题解析
23. 如图，点A，E，F，C在同一条直线上， $A E = C F$ ，过点E，F分别作 $D E ⊥ A C$ ， $B F ⊥ A C$ ， $A B ∥ C D$ ，求证：AC与BD互相平分．

查看试题解析
24. 如图，E是 $∠ A O B$ 的平分线上一点， $E C ⊥ O B$ ， $E D ⊥ O A$ ， C、D是垂足，连接CD交OE于点F，若 $∠ A O B = 6 0^{∘}$ ．

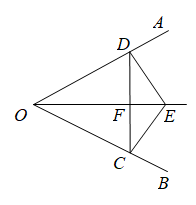(1)、求证： $△ O C D$ 是等边三角形；

(2)、若 $E F = 1$ ，求线段OF的长．

查看试题解析
25. 数学兴趣小组在活动时，老师提出了这样一个问题：
如图1，在 $△ A B C$ 中， $A B = 6$ ， $A C = 10$ ， D是BC的中点，求BC边上的中线AD的取值范围．

(1)、【阅读理解】
小明在组内经过合作交流，得到了如下的解决方法：

如图1，延长AD到E点，使 $D E = A D$ ，连接BE．根据可以判定 $△ A D C ≌$ ，得出 $A C =$ ．

这样就能把线段AB、AC、 $2 A D$ 集中在 $△ A B E$ 中．利用三角形三边的关系，即可得出中线AD的取值范围是．

(2)、【方法感悟】
当条件中出现“中点”、“中线”等条件时，可以考虑做“辅助线”——把中线延长一倍，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中，这种做辅助线的方法称为“中线加倍”法．

【问题解决】

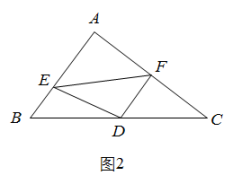
如图2，在 $△ A B C$ 中， $∠ A = 9 0^{∘}$ ， D是BC边的中点， $∠ E D F = 9 0^{∘}$ ， DE交AB于点E，DF交AC于点F，连接EF，求证： $B E^{2} + C F^{2} = E F^{2}$ ．

(3)、【问题拓展】
如图3， $△ A B C$ 中， $∠ B = 9 0^{∘}$ ， $A B = 3$ ， AD是 $△ A B C$ 的中线， $C E ⊥ B C$ ， $C E = 5$ ，且 $∠ A D E = 9 0^{∘}$ ．直接写出AE的长＝．

查看试题解析