山东省威海乳山市（五四制）2021-2022学年七年级上学期期中考试数学试题
试卷更新日期：2022-09-22 类型：期中考试
一、单选题
-
1. 手机作为人们日常通讯的主要工具，其背后离不开通讯运营商的技术支持，下图展现的是我国四大通讯运营商的企业图标，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 如图，是工人师傅用同一种材料制成的金属框架，已知 ， ， ， 其中的周长为24cm， ， 则制成整个金属框架所需这种材料的总长度为（ ）
A、45cm B、48cm C、51cm D、54cm3. 下列条件中，能判定△ABC≌△DEF的是（ ）A、AB=DE，BC=EF，∠A=∠D B、∠A=∠D，∠C=∠F，AC=EF C、∠B=∠E，∠A=∠D，AC=EF D、∠B=∠E，∠A=∠D，AB=DE4. 如图①是一张画有小方格的等腰直角三角形纸片，将图①按箭头方向折叠成图②，再将图②按箭头方向折叠成图③，再沿直线l剪掉直线l上方的三角形部分，最后把剩余部分展开，所得到的图形是（ ）．
A、
B、
C、
D、
5. 下列图形：①两个正方形；②底边相等的两个等腰三角形；③每边都是2cm的两个三角形；④半径都是1.5cm的两个圆．其中是一对全等图形的有（ ）A、1个 B、2个 C、3个 D、4个6. 等腰三角形的一个角是50°，则一腰上的高与底边的夹角是（ ）A、25° B、40° C、25°或40° D、25°或60°7. 下面是“求作∠AOB的角平分线”的尺规作图过程（ ）已知：钝角∠AOB．
求作：∠AOB的角平分线．
作法：
①在OA和OB上，分别截取OD，OE，使OD=OE；
②分别以D，E为圆心，大于DE的长为半径作弧，交∠AOB内部的点C；
③作射线OC．
所以，射线OC就是所求作的∠AOB的角平分线．
上述尺规作图的依据是（ ）
A、ASA B、SAS C、AAS D、SSS8. 折纸是我国的传统文化，折纸不仅和自然科学结合在一起，还发展出了折纸几何学，成为现代几何学的一个分支．如图，将一长方形纸条首先沿EF进行第一次折叠，使得C，D两点落在 ， 的位置，再将纸条沿GF折叠（GF与BC在同一直线上），使得 ， 分别落在 ， 的位置．若3∠ EFB=∠EF ， 则∠GEF的度数为（ ）
A、30° B、36° C、45° D、60°9. 如图为5×5的方格，点A，B，C均在格点上，点P在方格的其它格点上，且点A，B，C，P构成一个轴对称的点阵图，则符合条件的P点的位置有（ ）
A、5个 B、4个 C、3个 D、2个10. 如图，ABCD是一张长方形纸片，将AD，BC折起，使A、B两点重合于CD边上的P点，然后压平得折痕EF与GH．若PE＝8cm，PG＝6cm，EG＝10cm，则长方形纸片ABCD的面积为（ ）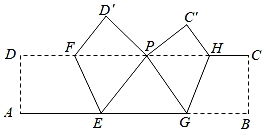
A、105.6cm2 B、110.4cm2 C、115.2cm2 D、124.8cm2二、多选题
-
11. 下列四组数不能作为直角三角形三边长的是（ ）A、4，8，9 B、1，1，2 C、4.5，6，7.5 D、12. 如图，△ABC是等边三角形，AP平分∠BAC，AQ=PQ，PR⊥AB于点R，PS⊥AC于点S．下列结论正确的是（ ）
A、 B、AS=AR C、QP∥AR D、△BRP≌△QSP三、填空题
-
13. 如图， ， 则线段是中边上的高．
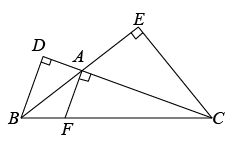14. 一根长度为16cm的圆珠笔，放在一个长宽高分别为3cm ，4cm，12cm的长方体笔筒内，则圆珠笔至少有cm 露在笔筒外面．15. 如图，△ABC≌△DBE，∠C=45°，∠ABE=70°，∠ABD=40°，则∠D的度数为 ．
16. 已知△ABC的三边长分别为5，7，8，△DEF的三边分别为5，2x，3x﹣5，若两个三角形全等，则x= ．17. 如图，在△ABC中，AB＝12，AC＝8，AD是BC边上的中线，则AD的取值范围是 ．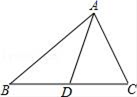
18. 如图是按照一定规律“生长”的“勾股树”：
经观察可以发现：图（1）中共有3个正方形，图（2）在图（1）的基础上增加了4个正方形，图（3）在图（2）的基础上增加了8个正方形，……，照此规律“生长”下去，图（6）应在图（5）的基础上增加的正方形的个数是 ．
四、解答题
-
19. 如图，∠BAC=∠DAC，∠B=∠D．写出∠1=∠2的理由．
20. 从“①AD=AE；②∠ABE=∠ACD；③FB=FC”三个条件中选择一个，补充在下面问题的横线上，并对问题进行解答．如图，在△ABC中，∠ABC=∠ACB，点D，E分别在边AB，AC上，连接BE，CD，BE与CD交于点F，增加条件 ▲ ， 可以得出BE=CD．请写出BE=CD的理由．
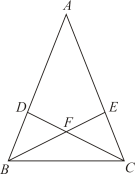21. 如图，小明的家（A点）在一条河流（直线l）的一侧，在河流l同侧有一个公园（B点），点A，B都在格点上．小明要带着他的狗先到河边喝水，然后再去公园．
(1)、要使小明所走的路线最短，请你确定出喝水的地点；（要求：保留画图痕迹）(2)、若每个小方格的边长都表示200米，求出小明所走最短路线的长度．22. 如图，△ABC是等边三角形，点D在BC边上，连接AD，点E在AB的延长线上，点F在AC边上，∠EDF=120°，ED= DF．写出AD与BC垂直的理由．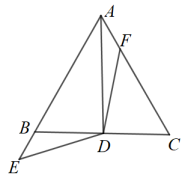
23. 【模型呈现】如图①，D是△ABC边BC的中点，则 ．
(1)、【模型变式】
如图②，若MN∥AB，直接写出图中面积相等的三角形： ．
(2)、【模型应用】如图③，在四边形ABCD中，过A点画直线AF，交BC于点F，使得AF能将四边形ABCD的面积二等分．请简要写出画法，并写明理由．
24. 在△ABC中，∠A=90°，AB=AC，点D是边BC的中点．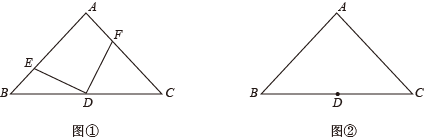
(1)、如图①，若点E，F分别在边AB，AC上，DE⊥DF，写出BE=AF的理由；(2)、若点E，F分别在AB，CA的延长线，DE⊥DF．请先在图②上补全图形，再解决问题： BE与AF是否仍然相等？若相等，写出理由；若不相等，写出新的数量关系及理由．25. 【备用性质】对于正方形ABCD，具有下面的性质：
①四边都相等，即：AB=BC=CD=AD；
②四角都是直角，即：∠ABC=∠BCD=∠CDA=∠DAB =90°；
③对角线相等且互相平分，即：AC=BD=2AO=2BO
④对角线互相垂直，即：AC⊥BD．
【问题解决】
如图，点G是正方形ABCD对角线CA延长线上一点，以线段AG为边作正方形AGFE，EB与GD交于点H．
(1)、写出△EAB≌△GAD的理由；(2)、若BD=12，AG=2，求EB的长．