山东省泰安市肥城市2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-09-22 类型:期中考试
一、单选题
-
1. 下列四个图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )
2. 如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D、点E、点F,△ABC中AC边上的高是( )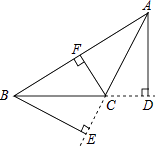 A、CF B、BE C、AD D、CD3. 下列一组数:﹣2.5,0,﹣3 , , ,0.080080008,1.121121112…其中无理数有( )A、0个 B、1个 C、2个 D、3个4. 如图 , , 下列条件中不能判定的是( )
A、CF B、BE C、AD D、CD3. 下列一组数:﹣2.5,0,﹣3 , , ,0.080080008,1.121121112…其中无理数有( )A、0个 B、1个 C、2个 D、3个4. 如图 , , 下列条件中不能判定的是( )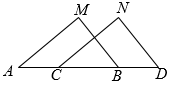 A、 B、 C、 D、5. 如图,一副三角板叠在一起,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,AC与DE交于点M,如果 ,则 的度数为( )
A、 B、 C、 D、5. 如图,一副三角板叠在一起,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,AC与DE交于点M,如果 ,则 的度数为( ) A、80 B、85 C、90 D、956. 已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )A、5 B、25 C、25或7 D、77. 下列条件中,不能判定 为直角三角形的是( )A、 B、 C、 D、 , ,8. 下列说法:①36的平方根是6;②;③0.1是0.01的平方根;④81的算术平方根是 . 其中正确的说法有( )A、0个 B、1个 C、2个 D、3个9. 如图,有一块直角三角形纸片,两直角边 , . 现将直角边沿直线折叠,使它落在斜边上,且与重合,则的大小为( )
A、80 B、85 C、90 D、956. 已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )A、5 B、25 C、25或7 D、77. 下列条件中,不能判定 为直角三角形的是( )A、 B、 C、 D、 , ,8. 下列说法:①36的平方根是6;②;③0.1是0.01的平方根;④81的算术平方根是 . 其中正确的说法有( )A、0个 B、1个 C、2个 D、3个9. 如图,有一块直角三角形纸片,两直角边 , . 现将直角边沿直线折叠,使它落在斜边上,且与重合,则的大小为( ) A、2cm B、3cm C、4.8cm D、5cm10. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
A、2cm B、3cm C、4.8cm D、5cm10. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.
 A、4 B、3 C、2 D、111. 如图,在 中, 垂直平分 ,分别交 于 ,连接 平分 ,交 于 ,若 ,则 的度数为( )
A、4 B、3 C、2 D、111. 如图,在 中, 垂直平分 ,分别交 于 ,连接 平分 ,交 于 ,若 ,则 的度数为( ) A、58° B、63° C、67° D、70°12. 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了上图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是( )
A、58° B、63° C、67° D、70°12. 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了上图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是( ) A、1 B、2021 C、2020 D、2019
A、1 B、2021 C、2020 D、2019二、填空题
-
13. 在等腰三角形中,已知一个角为40°,那么另两个角的度数是.14. 若一个正数的两个不同平方根分别是和 , 则这个数是 .15. 如图是一块地的平面示意图,已知AD=4 m,CD=3 m,AB=13 m,BC=12 m,∠ADC=90°,则这块地的面积为m2.
 16. 如图,AB∥EF,∠C=∠D=85°,CF=BD,若∠A=40°,则∠EFD= .
16. 如图,AB∥EF,∠C=∠D=85°,CF=BD,若∠A=40°,则∠EFD= .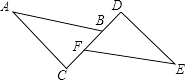 17. 如图,的斜边的垂直平分线与交于点 , , , 则的面积为 .
17. 如图,的斜边的垂直平分线与交于点 , , , 则的面积为 . 18. 如图所示,是长方形地面,长 , 宽 , 中间整有一堵砖墙高 , 一只蚂蚁从点爬到点,它必须翻过中间那堵墙,则它至少要走 .
18. 如图所示,是长方形地面,长 , 宽 , 中间整有一堵砖墙高 , 一只蚂蚁从点爬到点,它必须翻过中间那堵墙,则它至少要走 .
三、解答题
-
19. 如图,已知∠AOB及点E、F,在∠AOB的内部求作点P,使点P到OA、OB的距离相等,且PE=PF.(请尺规作图,保留作图痕迹,并写结论)
 20. 如图, 中,点D、E在边 上, , .求证: .
20. 如图, 中,点D、E在边 上, , .求证: . 21. 如图,是等边三角形,D是上一点, , , 试判断的形状并说明理由.
21. 如图,是等边三角形,D是上一点, , , 试判断的形状并说明理由. 22. 在8×8的方格纸中,设小方格的边长为1.
22. 在8×8的方格纸中,设小方格的边长为1.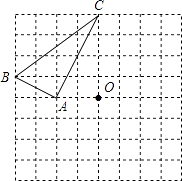 (1)、请判断△ABC的形状并说明理由.
(1)、请判断△ABC的形状并说明理由.
(2)、画出△ABC以CO所在直线为对称轴的对称图形△A′B′C′,并在所画图中标明字母.
23. 已知 , 平分交于 , 于 , , 连结 , 判断的形状,并说明理由.


