山东省德州市陵城区2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-09-22 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，检测4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数．从轻重的角度看，最接近标准的是（　　）

A、 B、 C、 D、

查看试题解析
2. $- \frac{1}{8}$ 的倒数的相反数是（）

A、8 B、－8 C、 $\frac{1}{8}$ D、 $- \frac{1}{8}$

查看试题解析
3. 若两个有理数a、b在数轴上表示的点如图所示，则下列各式中正确的是（）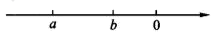

A、a＞b B、|a|＜|b| C、-a＞-b D、-a＜|b|

查看试题解析
4. 下列各组数中，① $- (- \frac{1}{2})$ 和 $- | - 2 |$ ；② ${(- 1)}^{2}$ 和 $- 1^{2}$ ；③ $2^{3}$ 和 $3^{2}$ ；④ ${(- 2)}^{3}$ 和 $2^{3}$ ，互为相反数的有（）

A、①③ B、②④ C、②③④ D、③④

查看试题解析
5. 某商品原价为 $a$ 元，以 $(\frac{7}{10} a - 5)$ 元出售，则下列说法中，能正确表达该商品出售价格的是（）

A、先打3折，再降5元 B、先打7折，再降5元 C、先降5元，再打3折 D、先降5元，再打7折

查看试题解析
6. 在算式（－2）□（－3）的□中填上运算符号，使结果最小，运算符号是（）

A、加号 B、减号 C、乘号 D、除号

查看试题解析
7. 将 $(x + y) - 2 (x + y)$ 化简得（）

A、 $x + y$ B、 $x - y$ C、 $- x + y$ D、 $- x - y$

查看试题解析
8. 若 $| a | = 4$ ， $| b | = 2$ ，且 $a + b$ 的绝对值与相反数相等，则 $a - b$ 的值是（）

A、 $- 2$ B、 $- 6$ C、 $- 2$ 或 $- 6$ D、2或6

查看试题解析
9. 下列说法中错误的是（　　）

A、如果a＞0，b＜0且a+b＞0，则|a|＞|b| B、如果a＜0，b＞0，则a-b＜0 C、如果a+b＜0，且a，b同号，那么a＞0，b＞0 D、如果a＜0，b＜0且|a|＞|b|，则a-b＜0

查看试题解析
10. 现规定一种新运算“*”：a*b＝（a﹣b）﹣|b﹣a|．则（﹣3）*2的值为（ )

A、10 B、0 C、-10 D、12

查看试题解析
11. 如图所示，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字0所对应的点与数轴上的数－2所对应的点重合，再让圆沿着数轴按顺时针方向滚动，那么数轴上的数－2020将与圆周上的哪个数字重合（）

A、0 B、1 C、2 D、3

查看试题解析
12. 将两边长分别为a和b（a＞b）的正方形纸片按图1、图2两种方式置于长方形ABCD中，（图1、图2中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1上中阴影部分的周长为C₁ ，图2中阴部分的周长为C₂ ，则C₁－C₂的值（）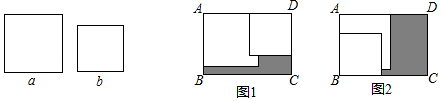

A、0 B、a－b C、2a－2b D、2b－2a

查看试题解析

二、填空题

13. 6月11日，国家航天局在北京举行天问一号探测器成功着陆火星首批科学影像图揭幕仪式，公布了着陆点全景、火星地形地貌、“中国印迹”和“着巡合影”等影像图，标志着我国首次火星深测任务取得圆满成功．人类为什么热衷登录火星，原因之一就是火星距离地球足够“近”，火星距离地球最近时能达到55000000公里，将55000000用科学记数法表示为．

查看试题解析
14. 已知a，b互为相反数，c，d互为倒数，则代数式 $5 (a + b) - 4 c d$ 的值为．

查看试题解析
15. 已知 $2 a - 3 b + 2 = 0$ ，则 $6 b - 4 a - 5 =$ ．

查看试题解析
16. 若代数式﹣（3x³ym－1）＋3（xny＋1）（x，y≠0，1）经过化简后的结果等于4，则m﹣n的值是．

查看试题解析
17. 2021加上它的 $\frac{1}{2}$ 得到一个数，再加上所得的数的 $\frac{1}{3}$ 又得到一个数，再加上这次得数的 $\frac{1}{4}$ 又得到一个数…，以此类推，一直加到上一次得数的 $\frac{1}{2021}$ ，最后得到的数是．

查看试题解析
18. 在纸面上有一数轴，折叠纸面，使数 $- 3$ 表示的点与数 $7$ 表示的点重合，则
①数 $3$ 表示的点与数表示的点重合；
②若数轴上 $A$ 、 $B$ 两点之间距离为 $11$ ．（ $A$ 在 $B$ 的左侧），且 $A$ 、 $B$ 两点经折叠后重合，则点 $A$ 表示的数是，点 $B$ 表示的数是．

查看试题解析

三、解答题

19. 计算：

(1)、 $(\frac{1}{4} + \frac{3}{8} - \frac{7}{12}) \div \frac{1}{24}$ ；

(2)、 ${(- 1)}^{2021} \times | 1 \frac{1}{2} | - (0.5) \div (- \frac{1}{3})$ ．

查看试题解析
20. 为了有效控制酒后驾驶，广州交警的汽车在一条东西方向的公路上巡逻，约定向东为正方向，从出发点A开始所走的路程为（单位：千米）：+14．﹣9，+8，﹣7，+13，﹣6，+12，﹣5．

(1)、请你帮忙确定交警最后所在地相对于A地的方位？

(2)、若汽车每千米耗油0.2升，如果队长命令他马上返回出发点，这次巡逻（含返回）共耗油多少升？

查看试题解析
21. 请根据图示的对话解答下列问题．

(1)、求：a、b、c的值；

(2)、计算9﹣2^a+3b﹣c的值．

查看试题解析
22. 化简求值：已知 $A = - a^{2} + 2 a b + 2 b^{2}$ ， $B = 2 a^{2} - a b - 2 b^{2}$ ，当 $a = - \frac{1}{2}$ ， $b = 1$ 时，求 $2 A + B$ 的值．

查看试题解析
23. 利用运算律有时能进行简便计算．
例1 98×12=（100-2） ×12=1 200-24=1 176；
例2 -16×233+17×233=（-16+17）×233=233．
请你参考黑板中老师的讲解，用运算律简便计算：

(1)、 $999 \times (- 15)$ ；

(2)、 $999 \times 118 \frac{4}{5} + 999 \times (- \frac{1}{5}) - 999 \times 18 \frac{3}{5}$

查看试题解析
24. 若在一个 $3 \times 3$ 的方格中填写了9个不同的数字（正整数），且使得每行、每列及每条对角线上的三个数字之和均相等，则称这个 $3 \times 3$ 的方格为“三阶幻方”；

(1)、如图1是一个三阶幻方，则 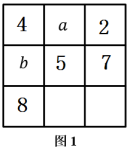$a =$ ； $b =$ ；

(2)、在图2中空格处填上合适的数字，使它构成一个三阶幻方；

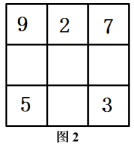(3)、已知 $m 、 n$ 为正整数，且 $m > 4 n$ ，在下面的方格中填写适当的代数式，使它能构成一个三阶幻方
$m + 3 n$

$m$
$m + 2 n$
$m - n$
$m - 3 n$

查看试题解析
25. 为丰富校园体育生活，某校增设网球兴趣小组，需要采购某品牌网球训练拍30支，网球x筒（x＞30）．经市场调查了解到该品牌网球拍定价100元/支，网球20元/筒．现有甲、乙两家体育用品商店有如下优惠方案：
甲商店：买一支网球拍送一筒网球；
乙商店：网球拍与网球均按则90%付款，

(1)、方案一：到甲商店购买，需要支付元；方案二：到乙商店购买，需要支付元（用含x的代数式表示）

(2)、若x＝100，请通过计算说明学校采用以上哪个方案较为优惠．

(3)、若x＝100，如果到甲店购买30支球拍（送30筒球），剩余的网球到乙店购买，能更省钱吗？如果可以省钱，请直接写出比方案一省多少钱？

查看试题解析

$m + 3 n$
	$m$	$m + 2 n$
$m - n$		$m - 3 n$