四川省德阳广汉市2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2022-09-21 类型:期中考试
一、单选题
-
1. 下列图形绕某点旋转180°后,不能与原来图形重合的是( )A、
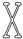 B、
B、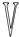 C、
C、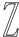 D、
D、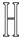 2. 下列方程中是关于x的一元二次方程的是( )A、x2+ =0 B、ax2+bx+c=0 C、(x-1)(x+2)=1 D、3x-2xy-5y2=03. 用配方法解下列方程时,配方有错误的是( )A、2m2+m﹣1=0化为 B、x2﹣6x+4=0化为(x﹣3)2=5 C、2t2﹣3t﹣2=0化为 D、3y2﹣4y+1=0化为4. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C , 连接AA',若∠1=25°,则∠BAA'的度数是( )
2. 下列方程中是关于x的一元二次方程的是( )A、x2+ =0 B、ax2+bx+c=0 C、(x-1)(x+2)=1 D、3x-2xy-5y2=03. 用配方法解下列方程时,配方有错误的是( )A、2m2+m﹣1=0化为 B、x2﹣6x+4=0化为(x﹣3)2=5 C、2t2﹣3t﹣2=0化为 D、3y2﹣4y+1=0化为4. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C , 连接AA',若∠1=25°,则∠BAA'的度数是( )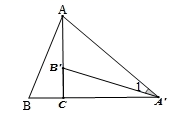 A、70° B、65° C、60° D、55°5. 二次函数y=x2-1的图象可由下列哪个函数图象向右平移2个单位,向下平移2个单位得到( )A、 B、 C、 D、6. 二次函数y=ax2+bx+c的y与x的部分对应值如表,则下列判断中正确的是( )
A、70° B、65° C、60° D、55°5. 二次函数y=x2-1的图象可由下列哪个函数图象向右平移2个单位,向下平移2个单位得到( )A、 B、 C、 D、6. 二次函数y=ax2+bx+c的y与x的部分对应值如表,则下列判断中正确的是( )x
…
0
1
3
4
…
y
…
2
4
2
-2
…
A、抛物线开口向上 B、y最大值为4 C、当x>1时,y随着x的增大而减小 D、当0<x<2时,y>27. 已知点A(-3,y1),B(2,y2),C(3,y3)在抛物线y=2x2-4x+c上,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y2>y3>y18. 如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为 , 求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( ) A、 B、 C、 D、9. 在同一坐标系内,一次函数与二次函数的图像可能是( )A、
A、 B、 C、 D、9. 在同一坐标系内,一次函数与二次函数的图像可能是( )A、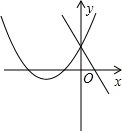 B、
B、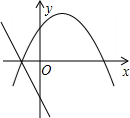 C、
C、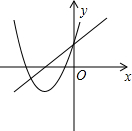 D、
D、 10. 如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
10. 如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )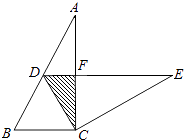 A、30,2 B、60,2 C、60, D、60,11. 如图,在矩形中, , .将矩形绕点沿顺时针方向旋转后,得到矩形(点、、的对应点分别为点、、).动点从点开始沿运动到点后停止,动点从点开始沿运动到点后停止,这两点的运动速度均为每秒个单位.若点和点同时开始运动,运动时间为(秒),的面积为 , 则能够正确反映与之间的函数关系的图象大致是( ).
A、30,2 B、60,2 C、60, D、60,11. 如图,在矩形中, , .将矩形绕点沿顺时针方向旋转后,得到矩形(点、、的对应点分别为点、、).动点从点开始沿运动到点后停止,动点从点开始沿运动到点后停止,这两点的运动速度均为每秒个单位.若点和点同时开始运动,运动时间为(秒),的面积为 , 则能够正确反映与之间的函数关系的图象大致是( ). A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
12. 方程 的根是.13. 若函数y=(m-2)x|m|+2x+1是关于x的二次函数,则m的值为.14. 若m,n是方程x2+x-1=0的两根,则式子的值是.15. 今年福安白云山千古冰臼群迎来旅游高峰,前三天的游客人数共计约5.1万人,其中第一天的游客人数是1.2万人,假设每天游客增加的百分率相同,且设为 , 则根据题意可列方程为.16. 如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,则点E与点C之间的距离是cm.
 17. 如图,已知二次函数 的图象与 轴交于点 ,与 轴的交点 在 和 之间(不包括这两点),对称轴为直线 .下列结论:① ;② ;③ ;④ ;⑤ .其中正确的是.
17. 如图,已知二次函数 的图象与 轴交于点 ,与 轴的交点 在 和 之间(不包括这两点),对称轴为直线 .下列结论:① ;② ;③ ;④ ;⑤ .其中正确的是.
三、解答题
-
18. 解下列方程(1)、x2-6x=-9(2)、x2-3x-7=0(用公式法解)19. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
 (1)、请画出△ABC绕原点旋转180°的△A2B2C2;并写出各点的坐标.(2)、在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.20. 如图,直线 和抛物线 都经过点 , .
(1)、请画出△ABC绕原点旋转180°的△A2B2C2;并写出各点的坐标.(2)、在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.20. 如图,直线 和抛物线 都经过点 , .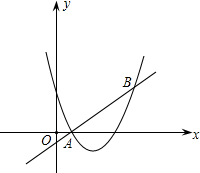 (1)、求m的值和抛物线的解析式;(2)、求不等式 的解集 直接写出答案21. 已知关于x的方程x2-(k+2)x+2k=0.(1)、求证:k取任何实数值,方程总有实数根;(2)、若Rt△ABC斜边长a=3,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.22. 商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件,据此规律,请回答:
(1)、求m的值和抛物线的解析式;(2)、求不等式 的解集 直接写出答案21. 已知关于x的方程x2-(k+2)x+2k=0.(1)、求证:k取任何实数值,方程总有实数根;(2)、若Rt△ABC斜边长a=3,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.22. 商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件,据此规律,请回答:
(1)、当每件商品售价定为140元时,每天可销售多少件商品?商场获得的日盈利是多少?(2)、在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元,商场日盈利可达1500元?23. 将两个全等的直角三角形ABC和DBE按图 方式摆放,其中 , ,点E落在AB上,DE所在直线交AC所在直线于点F.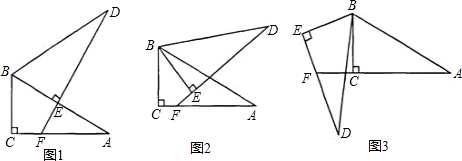 (1)、求证: ;(2)、若将图 中的 绕点B按顺时针方向旋转角a,且 ,其他条件不变,如图 请你直接写出 与DE的大小关系: 填“ ”或“ ”或“ ”(3)、若将图 中 的绕点B按顺时针方向旋转角 ,且 ,其他条件不变,如图 请你写出此时AF、EF与DE之间的关系,并加以证明.24. 如图所示,在平面直角坐标系xOy中,有AB为斜边的等腰直角三角形ABC,其中点A(0,2),点C(﹣1,0),抛物线y=ax2+ax﹣2经过B点.
(1)、求证: ;(2)、若将图 中的 绕点B按顺时针方向旋转角a,且 ,其他条件不变,如图 请你直接写出 与DE的大小关系: 填“ ”或“ ”或“ ”(3)、若将图 中 的绕点B按顺时针方向旋转角 ,且 ,其他条件不变,如图 请你写出此时AF、EF与DE之间的关系,并加以证明.24. 如图所示,在平面直角坐标系xOy中,有AB为斜边的等腰直角三角形ABC,其中点A(0,2),点C(﹣1,0),抛物线y=ax2+ax﹣2经过B点. (1)、求B点的坐标;(2)、求抛物线的解析式;(3)、在抛物线上是否存在点N(点B除外),使得△ACN仍然是以AC为直角边的等腰直角三角形?若存在,求点N的坐标;若不存在,请说明理由.
(1)、求B点的坐标;(2)、求抛物线的解析式;(3)、在抛物线上是否存在点N(点B除外),使得△ACN仍然是以AC为直角边的等腰直角三角形?若存在,求点N的坐标;若不存在,请说明理由.