四川省成都市温江区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-21 类型:期中考试
一、单选题
-
1. 下列方程中,① , ② , ③ , ④ , 是一元二次方程的有( )A、1个 B、2个 C、3个 D、4个2. 已知 ,下列变形错误的是( )
A、 B、 C、 D、3. 如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )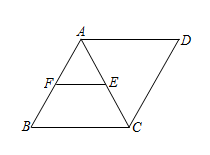 A、24 B、18 C、12 D、94. 如图,小明从路灯下A处,向前走了5米到达D处,在D处发现自己在地面上的影子长是2米,如果小明的身高为1.6米,那么路灯离地面的高度是( )米.
A、24 B、18 C、12 D、94. 如图,小明从路灯下A处,向前走了5米到达D处,在D处发现自己在地面上的影子长是2米,如果小明的身高为1.6米,那么路灯离地面的高度是( )米.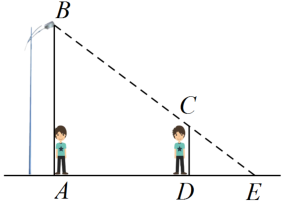 A、4.6 B、5.6 C、7.5 D、8.55. 在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )A、 B、 C、 D、6. 如图所示的几何体,它的左视图是( )
A、4.6 B、5.6 C、7.5 D、8.55. 在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )A、 B、 C、 D、6. 如图所示的几何体,它的左视图是( )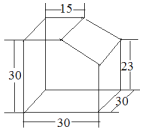 A、
A、 B、
B、 C、
C、 D、
D、 7. 等腰三角形三边长分别为a,b,3,且a,b是关于x的一元二次方程x2﹣8x﹣1+m=0的两根,则m的值为( )A、15 B、16 C、15或17 D、16或178. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠19. 试验园的形状是长15米、宽8米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为110平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意列方程为( )
7. 等腰三角形三边长分别为a,b,3,且a,b是关于x的一元二次方程x2﹣8x﹣1+m=0的两根,则m的值为( )A、15 B、16 C、15或17 D、16或178. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠19. 试验园的形状是长15米、宽8米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为110平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意列方程为( ) A、(15+2x)(8+x)=110 B、(15﹣2x)(8﹣x)=110 C、(15+x)(8+2x)=110 D、(15﹣x)(8﹣2x)=110
A、(15+2x)(8+x)=110 B、(15﹣2x)(8﹣x)=110 C、(15+x)(8+2x)=110 D、(15﹣x)(8﹣2x)=110二、多选题
-
10. 如图,∠1=∠2,则下列各式能说明ABC∽ADE的是( )
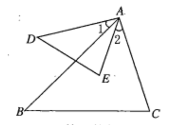 A、∠D=∠B B、∠E=∠C C、 D、
A、∠D=∠B B、∠E=∠C C、 D、三、填空题
-
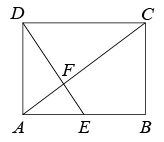
11. 已知: ,则 的值是.12. 为了估计池塘里有多少条鱼,先从湖里捕捞100条鱼记上标记,然后放回池塘去,经过一段时间,待有标记的鱼完全混合后,第二次再捕捞200条鱼,发现有5条鱼有标记,那么你估计池塘里大约有条鱼.13. 已知P是线段的黄金分割点 , 且 , 则长为(cm).14. 如图,在矩形中,是边的中点,连接交对角线于点 , 若 , , 则的长为.
 15. 一元二次方程的两根为和 , 则.16. 如图,∠A=∠B=90°,AD=2,BC=3,点P在线段AB上,且PB=5,若△PAD与△PBC相似,则AP的长为.
15. 一元二次方程的两根为和 , 则.16. 如图,∠A=∠B=90°,AD=2,BC=3,点P在线段AB上,且PB=5,若△PAD与△PBC相似,则AP的长为.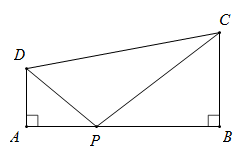 17. 有正面分别标有数字-2、-1、0、1、2的五张不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为m,则使关于x的方程+x-m=0有实数解且关于x的不等式组有整数解的的概率为.18. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2.运动过程中点D到点O的最大距离是.
17. 有正面分别标有数字-2、-1、0、1、2的五张不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为m,则使关于x的方程+x-m=0有实数解且关于x的不等式组有整数解的的概率为.18. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2.运动过程中点D到点O的最大距离是.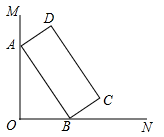 19. 已知:如图,等腰直角 , , , 点D为外一点, , 连接CD, , , BC的长为.
19. 已知:如图,等腰直角 , , , 点D为外一点, , 连接CD, , , BC的长为.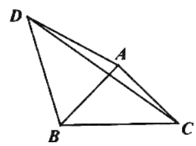
四、解答题
-
20. 解方程:(1)、;(2)、;(3)、.21. 如图,网格中每个小正方形的边长均为1,且点A,B,C,P均为格点.
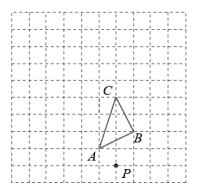 (1)、在网格中作图:以点P为位似中心,将△ABC的各边长放大为原来的两倍,A,B,C的对应点分别为A1 , B1 , C1;(2)、若点A的坐标为 , 点B的坐标为 , 则(1)中点C1的坐标为;(3)、求三角形A1B1C1的周长.22. 如图,矩形EFGH内接于 , 且边落在上,若 , , , , 求这个矩形的长和宽.
(1)、在网格中作图:以点P为位似中心,将△ABC的各边长放大为原来的两倍,A,B,C的对应点分别为A1 , B1 , C1;(2)、若点A的坐标为 , 点B的坐标为 , 则(1)中点C1的坐标为;(3)、求三角形A1B1C1的周长.22. 如图,矩形EFGH内接于 , 且边落在上,若 , , , , 求这个矩形的长和宽. 23. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
23. 某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: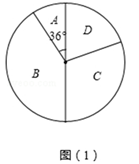
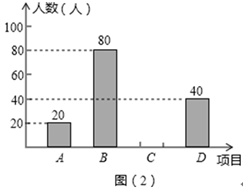 (1)、这次被调查的学生共有人;(2)、请你将条形统计图(2)补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)24. 已知关于的一元二次方程有两个实数根.(1)、求的取值范围;(2)、设x1 , x2是方程的两根,且x12+x22=23,求的值.25. 已知,如图所示的四边形ABCD为菱形,AC、BD交于O,AF⊥BC于F,交于点E.
(1)、这次被调查的学生共有人;(2)、请你将条形统计图(2)补充完整;(3)、在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)24. 已知关于的一元二次方程有两个实数根.(1)、求的取值范围;(2)、设x1 , x2是方程的两根,且x12+x22=23,求的值.25. 已知,如图所示的四边形ABCD为菱形,AC、BD交于O,AF⊥BC于F,交于点E.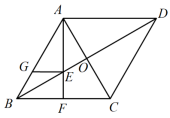 (1)、求证:(2)、求证:;(3)、过点E作 , 若 , 交于点G,若菱形ABCD的面积为 , 求的长.26. 某商场于今年年初以每件40元的进价购进一批商品.当商品售价为60元时,一月份销售64件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到100件.设二、三这两个月月平均增长率不变.(1)、求二、三这两个月的月平均增长率;(2)、从四月份起,商场决定采用降价促销,经调查发现,该商品每降价2元,销售量增加20件,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售,商场获利2240元?27. 某中学九年级数学课外学习小组某天下午实践活动课时,测量朝西教学楼前的旗杆的高度.如图所示,当阳光从正西方向照射过来时,旗杆的顶端A的影子落在教学楼前的草坪地C处,测得影长 , , , 与地面的夹角 , 在同一时刻,测得一根长为0.5m的直立竹竿的影长恰为1m.根据这些数据求旗杆的高度.
(1)、求证:(2)、求证:;(3)、过点E作 , 若 , 交于点G,若菱形ABCD的面积为 , 求的长.26. 某商场于今年年初以每件40元的进价购进一批商品.当商品售价为60元时,一月份销售64件.二、三月该商品十分畅销.销售量持续走高.在售价不变的基础上,三月底的销售量达到100件.设二、三这两个月月平均增长率不变.(1)、求二、三这两个月的月平均增长率;(2)、从四月份起,商场决定采用降价促销,经调查发现,该商品每降价2元,销售量增加20件,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售,商场获利2240元?27. 某中学九年级数学课外学习小组某天下午实践活动课时,测量朝西教学楼前的旗杆的高度.如图所示,当阳光从正西方向照射过来时,旗杆的顶端A的影子落在教学楼前的草坪地C处,测得影长 , , , 与地面的夹角 , 在同一时刻,测得一根长为0.5m的直立竹竿的影长恰为1m.根据这些数据求旗杆的高度.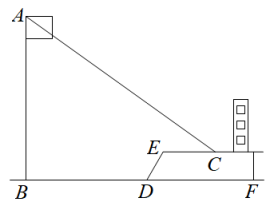 28. 如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
28. 如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y. (1)、求证:△DHQ△ABC;(2)、求y关于x的函数解析式;(3)、当x为何值时,△DHE为等腰三角形?
(1)、求证:△DHQ△ABC;(2)、求y关于x的函数解析式;(3)、当x为何值时,△DHE为等腰三角形?
-