四川省成都市龙泉驿区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程属于一元二次方程的是（）

A、 $x^{3} + 1 = x^{2}$ B、 $x^{2} + x - 1 = 0$ C、 $x - 3 = 0$ D、 $x + \frac{1}{x} - 4 = 0$

查看试题解析
2. 下列函数，其中y是x的反比例函数的是（）

A、 $y = 2 x - 1$ B、 $y = \frac{1}{x}$ C、 $y = \frac{1}{x^{2}}$ D、 $y = \frac{x}{3}$

查看试题解析
3. 反比例函数 $y = - \frac{3}{x}$ 的图象在（）

A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限

查看试题解析
4. 一元二次方程 $x^{2} + x - 3 = 0$ 的根的情况是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根

查看试题解析
5. 利用配方法解方程x²+2x＝1时，方程可变形为（）

A、(x+1)²＝2 B、(x﹣1)²＝2 C、(x+1)²＝0 D、(x﹣1)²＝0

查看试题解析
6. 为执行“两免一补”政策，某地区2006年投入教育经费2500万元，预计2008年投入3600万元．设这两年投入教育经费的年平均增长百分率为x，则下列方程正确的是（　　）

A、2500x²=3600 B、2500（1+x）²=3600 C、2500（1+x%）²=3600 D、2500（1+x）+2500（1+x）²=3600

查看试题解析
7. 反比例函数 $y = \frac{- 4}{x}$ 与一次函数 $y = x - 1$ 在同一坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
8. 如图，过原点的一条直线与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象分别交于A，B两点，若A点的坐标为 $(3 ， - 5)$ ，则B点的坐标为（）

A、 $(3 ， - 5)$ B、 $(- 5 ， 3)$ C、 $(- 3 ， 5)$ D、 $(- 5 ， - 3)$

查看试题解析
9. 电压为定值，电流 $I (A)$ 与电阻 $R (Ω)$ 成反比例，其函数图象如图所示，则电流I与电阻R之间的函数关系式为（）

A、 $I = \frac{48}{R}$ B、 $I = \frac{6}{R}$ C、 $I = \frac{8}{R}$ D、 $I = \frac{14}{R}$

查看试题解析
10. 已知反比例函数 $y = \frac{- a^{2} - 3}{x}$ （a为常数）图象上三个点的坐标分别是 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2}) ， C (x_{3} ， y_{3})$ ，其中 $x_{1} < 0 < x_{2} < x_{3}$ ，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系的是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析

二、填空题

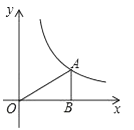
11. 若关于x的方程 $x^{2} + m x + 3 = 0$ 的一个根是 $x = 1$ ，则m的值为.

查看试题解析
12. 如图，过反比例函数 $y = \frac{k}{x}$ （x＞0）的图象上一点A作AB⊥x轴于点B，连接AO，若S_△_AOB=2，则k的值为．

查看试题解析
13. 在反比例函数 $y = \frac{k - 1}{x}$ 的图象的每一支上， $y$ 都随 $x$ 的增大而减少，则 $k$ 的取值范围是.

查看试题解析
14. 一元二次方程 $x^{2} - 3 x - 1 = 0$ 与 $x^{2} - x + 3 = 0$ 的所有实数根的和等于.

查看试题解析
15. 已知一元二次方程 $x^{2} - 3 x - 1 = 0$ 的两个根分别是 $x_{1} ， x_{2}$ ，则 $x_{1}^{2} x_{2} + x_{1} x_{2}^{2}$ 的值为.

查看试题解析
16. 若点 $A (m ， - 3)$ 在反比例函数 $y = \frac{6}{x}$ 的图象上，则当函数值 $y \geq - 3$ 时，自变量x的取值范围是.

查看试题解析
17. 如图，在反比例函数 $y = \frac{12}{x} (x > 0)$ 的图象上有点 $P_{1} ， P_{2} ， P_{3} ， P_{4} ， P_{5}$ ，它们的横坐标依次为2，4，6，8，10，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为 $S_{1} ， S_{2} ， S_{3} ， S_{4}$ ，则 $S_{1} + S_{2} + S_{3} + S_{4}$ 的值为.

查看试题解析
18. 如图，直线 $y = k x (k < 0)$ 与双曲线 $y = \frac{- 4}{x}$ 交于 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ 两点，则 $2 x_{1} y_{2} - 3 x_{2} y_{1}$ 的值为.

查看试题解析
19. 如图，直线 $y = - x + b$ 与y轴交于点A，与双曲线 $y = \frac{k}{x}$ 在第一象限交于B，C两点，且 $A B \cdot A C = 4$ ，则 $k =$ .

查看试题解析

三、解答题

20. 用配方法解一元二次方程： $x^{2} - 6 x + 5 = 0$ .

查看试题解析
21. 用适当的方法解一元二次方程.

(1)、 $x (x - 3) = - (x - 3)$ .

(2)、 $x^{2} + 4 x - 3 = 0$ .

查看试题解析
22. 已知关于x的方程x²-（3k+1）x+2k²+2k=0，

(1)、求证：无论k取何实数值，方程总有实数根．

(2)、若等腰△ABC的一边长为a=6，另两边长b，c恰好是这个方程的两个根，求此三角形的周长．

查看试题解析
23. 随着疫情在国内趋稳，却在国外迎来爆发期，多国采购中国防疫物资需求大增.某工厂建了1条口罩生产线生产口罩，开工第一天生产300万个，第三天生产432万个，若每天生产口罩的个数增长的百分率相同，请解答下列问题：

(1)、每天增长的百分率是多少？

(2)、经过一段时间后，工厂发现1条生产线最大产能是900万个/天，但如果每增加1条生产线，由于资源调配等原因每条生产线的最大产能将减少30万个/天，现该厂要保证每天生产口罩3900万个，应该建几条生产线？

查看试题解析
24. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于点 $A (1 ， 3) ， B (3 ， n)$ .

(1)、求这两个函数的表达式；

(2)、请结合图象直接写出不等式 $k x + b \geq \frac{m}{x}$ 的解集.

查看试题解析
25. 通过实验研究发现：初中生在体育课上运动能力指标（后简称指标）随上课时间的变化而变化.上课开始时，学生随着运动，指标开始增加，中间一段时间，指标保持平稳状态，随后随着体力的消耗，指标开始下降.指标y随时间x（分钟）变化的函数图象如图所示，当 $0 \leq x < 10$ 和 $10 \leq x < 20$ 时，图象是线段；当 $20 \leq x \leq 40$ 时，图象是反比例函数的一部分.

(1)、求这个分段函数的表达式；

(2)、杨老师想在一节课上进行某项运动的教学需要18分钟，这项运动需要学生的运动能力指标不低于48才能达到较好的效果，他的教学设计能实现吗？请说明理由.

查看试题解析
26. 先阅读理解下面的例题，再按要求解答下列问题：
例题：求代数式 $y^{2} + 6 y + 10$ 的最小值.
解： $y^{2} + 6 y + 10 = y^{2} + 6 y + 9 + 1 = (y + 3)^{2} + 1$
∵ $(y + 3)^{2} \geq 0$
∴ $(y + 3)^{2} + 1 \geq 1$
∴ $y^{2} + 6 y + 10$ 的最小值是1.

(1)、求代数式 $m^{2} + m + 3$ 的最小值；

(2)、为构建“五育并举”教育体系，某学校综合实践课程要在一块靠墙（墙长 $30 m$ ）的空地上建一个长方形的劳动田园 $A B C D$ ，田园一边靠墙，另三边用总长为 $40 m$ 的栅栏围成.如图，设 $A B = x (m)$ ，请问：当x取何值时，田园的面积最大？最大面积是多少？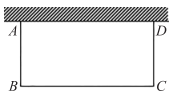

查看试题解析
27. 如图，点P是反比例函数 $y = \frac{k_{1}}{x} (k_{1} > 0 ， x > 0)$ 图象上一动点，过点P作x轴、y轴的垂线，分别交x轴、y轴于A，B两点，交反比例函数 $y = \frac{k_{2}}{x}$ （ $k_{2} < 0$ 且 $| k_{2} | > k_{1}$ ）的图象于E，F两点，连接 $O E ， O F ， E F$ .

(1)、四边形 $P E O F$ 的面积 $S_{1} =$ （用含 $k_{1} ， k_{2}$ 的式子表示）；

(2)、设P点坐标为 $(2 ， 3)$ .
①点E的坐标是（，），点F的坐标是（，）（用含 $k_{2}$ 的式子表示）；
②若 $△ O E F$ 的面积为 $\frac{15}{4}$ ，求反比例函数 $y = \frac{k_{2}}{x}$ 的解析式.

查看试题解析
28. 如图，一次函数 $y = - x + 4$ 的图象与反比例函数 $y = \frac{k}{x}$ （k为常数，且 $k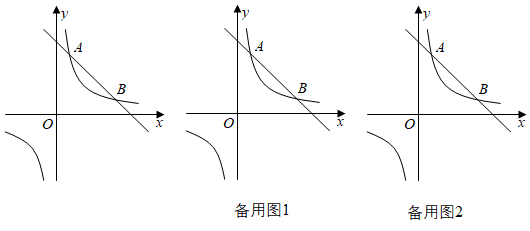 \neq 0$ ）的图象交与 $A (1 ， a)$ ， B两点.

(1)、求反比例函数的表达式及点B的坐标；

(2)、点P在反比例函数第三象限的图象上，使得 $△ P A B$ 的面积最小，求满足条件的P点坐标及 $△ P A B$ 面积的最小值；

(3)、设点M为x轴上一点，点N在双曲线上，以点A，B，M，N为顶点的四边形能否为平行四边形？若能，求出N点坐标：若不能，请说明理由.

查看试题解析