四川省成都市简阳市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-21 类型:期中考试
一、单选题
-
1. 已知两个相似三角形的相似比为1:4,则它们的周长比为( )A、1:4 B、4:1 C、1:2 D、1:162. 已知是线段的黄金分割点, , 若 , 则( )A、 B、 C、 D、3. 如图是一个几何体的三视图,该几何体是( )
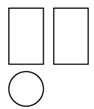 A、球 B、圆锥 C、圆柱 D、棱柱4. 若x=1是方程x2-2mx+3=0的解,则m的值为( )A、 B、2 C、 D、-25. 高4米的旗杆在水平地面上的影长为6米,此时测得附近一个建筑物的影长24米,则该建筑物的高度为( )A、10米 B、16米 C、26米 D、36米6. 正方形的一条对角线长为2,则正方形的周长为( )A、4 B、8 C、 D、7. 用配方法解方程 -4x+3=0,下列配方正确的是( )
A、球 B、圆锥 C、圆柱 D、棱柱4. 若x=1是方程x2-2mx+3=0的解,则m的值为( )A、 B、2 C、 D、-25. 高4米的旗杆在水平地面上的影长为6米,此时测得附近一个建筑物的影长24米,则该建筑物的高度为( )A、10米 B、16米 C、26米 D、36米6. 正方形的一条对角线长为2,则正方形的周长为( )A、4 B、8 C、 D、7. 用配方法解方程 -4x+3=0,下列配方正确的是( )
A、 =1 B、 =1 C、 =7 D、 =48. 顺次连接菱形各边中点所得到四边形一定是( )A、平行四边形 B、正方形 C、矩形 D、菱形9. 如图,l1∥l2∥l3 , 两条直线与这三条平行线分别交于点A、B、C和D、E、F,若 , 则的值为( )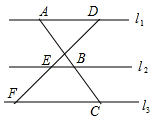 A、 B、 C、 D、10. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A、 B、 C、 D、10. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )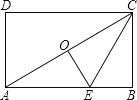 A、2 B、 C、 D、6
A、2 B、 C、 D、6二、填空题
-
11. 若 , 则的值等于 .12. 一元二次方程x2﹣2x=0的解是 .
13. 如图,将沿方向平移得到△ , 若的周长为 , 则四边形的周长为cm.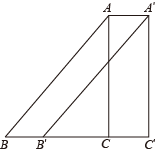 14. 如图,在A时测得某树的影长为4米,在B时测得该树的影长为9米,若两次日照的光线互相垂直,则该树的高度为米.
14. 如图,在A时测得某树的影长为4米,在B时测得该树的影长为9米,若两次日照的光线互相垂直,则该树的高度为米. 15. 设 , 是方程 的两个实数根,则 的值是 .16. 如图,菱形中, , , 过作于点 , 则的长为.
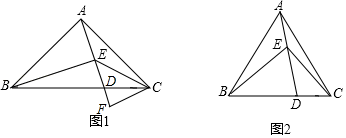
15. 设 , 是方程 的两个实数根,则 的值是 .16. 如图,菱形中, , , 过作于点 , 则的长为.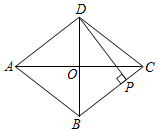 17. 有六张正面分别标有数字 , 0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,则抽取的卡片上的数字为不等式组的解的概率为.18. 如图,△ABC中,AD1=AB,D1D2=D1B,D2D3=D2B,…,照这样继续下去,D2020D2021=D2020B,且D1E1BC,D2E2BC,D2E3BC;…,D2021E2021BC,则=.
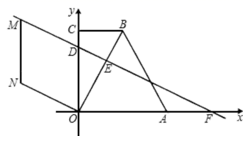
17. 有六张正面分别标有数字 , 0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,则抽取的卡片上的数字为不等式组的解的概率为.18. 如图,△ABC中,AD1=AB,D1D2=D1B,D2D3=D2B,…,照这样继续下去,D2020D2021=D2020B,且D1E1BC,D2E2BC,D2E3BC;…,D2021E2021BC,则=. 19. 如图,在矩形中, , 垂足为 , 动点分别在上,则的值为 , 的最小值为 .
19. 如图,在矩形中, , 垂足为 , 动点分别在上,则的值为 , 的最小值为 .
三、解答题
-
20.(1)、计算:.(2)、解方程:.21. 若关于x的一元二次方程x2+4x+2k=0有两个实数根,求k的取值范围及k的非负整数值.
22. 某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A、B、C依次表示这三个诵读材料),将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小华和小敏参加诵读比赛,比赛时小华先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小敏从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.(1)、小华诵读《弟子规》的概率是.(2)、请用列表法或画树状图法求小华和小敏诵读两个不同材料的概率.23. 某公司今年1月份的生产成本是400万元,由于改进技术,生产成本逐月下降,3月份的生产成本是361万元.假设该公司2、3、4月每个月生产成本的下降率都相同.
(1)、求每个月生产成本的下降率;(2)、请你预测4月份该公司的生产成本.
24. 李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.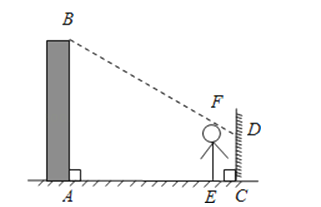 25. 如图,在矩形中,为边上一点, , 的平分线交的延长线于点.
25. 如图,在矩形中,为边上一点, , 的平分线交的延长线于点. (1)、求的度数;(2)、若 , 求的值;(3)、在(2)的条件下,连接 , 作交的延长线于点 , 当时,求的长.26. 某种茶具,平均每天可以销售20套,每套盈利44元,在每套降价幅度不超过22元的情况下,若每套降价1元,则每天可多售5套,设每套茶具降价元.(1)、求每套茶具降价元时每天销售茶具的套数;(2)、如果每天要盈利1600元,每套应降价多少元?
(1)、求的度数;(2)、若 , 求的值;(3)、在(2)的条件下,连接 , 作交的延长线于点 , 当时,求的长.26. 某种茶具,平均每天可以销售20套,每套盈利44元,在每套降价幅度不超过22元的情况下,若每套降价1元,则每天可多售5套,设每套茶具降价元.(1)、求每套茶具降价元时每天销售茶具的套数;(2)、如果每天要盈利1600元,每套应降价多少元?