四川省成都市都江堰市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-21 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，在数轴上，已知点 $Р$ 表示的数为 $- 3$ ，则点 $Р$ 到原点的距离是（）

A、 $- 3$ B、 $3$ C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 请根据“2021年全运会金牌前十排行榜”判断，金牌数这一组数据的中位数为（）
排名
1
2
3
4
5
6
7
8
9
10
代表团
山东
广东
浙江
江苏
上海
湖北
福建
湖南
四川
辽宁
金牌数
$58$
$54$
$44$
$42$
$36$
$27$
$25$
$25$
$22$
$22$

A、36 B、27 C、35.5 D、31.5

查看试题解析
3. 城市常住人口的增长是观察城市发展的重要数据，可以反映出一座城市的经济水平和发展潜力.目前，成都市城区常住人口为1334万，位列全国第六.将数据“1334万”用科学记数法可表示为（）

A、 $13.34 \times 1 0^{4}$ B、 $13.34 \times 1 0^{5}$ C、 $1.334 \times 1 0^{6}$ D、 $1.334 \times 1 0^{7}$

查看试题解析
4. 如图所示，两个几何体各由4个相同的小正方体搭成，比较两个几何体的三视图，可以得到的正确结论是（）

A、主视图不同 B、左视图不同 C、俯视图不同 D、主视图、左视图和俯视图都不相同

查看试题解析
5. 在下列式子中，运算结果等于 $\sqrt{5}$ 的是（）

A、 $\sqrt{2} + \sqrt{3}$ B、 $\sqrt{10} \times \frac{1}{2}$ C、 ${(\sqrt{5})}^{2}$ D、 $5 \div \sqrt{5}$

查看试题解析
6. 如果 $3 x = 4 y$ ，那么下列结论一定成立的是（）

A、 $x = 3$ ， $y = 4$ B、 $x = 4$ ， $y = 3$ C、 $x ： 4 = y ： 3$ D、 $x ： 3 = y ： 4$

查看试题解析
7. 一元二次方程 $2 x^{2} + 3 x = 3$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
8. 矩形、菱形、正方形都具有的性质是（　　）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分对角

查看试题解析
9. 在平面直角坐标系中，点 $P (- 2 ， 3 ）$ 关于直线 $x = 1$ 的对称点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 熊猫绿道，起于我市环山路玉堂街道，止于青城山镇，总长 $10$ 千米.甲、乙两人从绿道起点出发，沿着绿道徒步.已知甲每小时徒步 $a$ 千米，乙每小时徒步 $b$ 千米 $(a > b)$ ，他们各自走完绿道所用的时间，乙比甲多半小时.则符合题意的方程是（）

A、 $\frac{10}{b} - \frac{10}{a} = 30$ B、 $\frac{10}{a} - \frac{10}{b} = 30$ C、 $\frac{10}{b} - \frac{10}{a} = \frac{1}{2}$ D、 $\frac{10}{a} - \frac{10}{b} = \frac{1}{2}$

查看试题解析

二、填空题

11. 分式 $\frac{2}{1 - x}$ 有意义的条件是.

查看试题解析
12. 两个相似多边形对应边之比等于 $1 ： 2$ ，那么这两个相似多边形面积之比等于.

查看试题解析
13. 一次函数 $y = (k - 3) x + 2$ ，若 $y$ 随 $x$ 的增大而增大，则 $k$ 的取值范围是.

查看试题解析
14. 中国古代数学家刘徽在《九章算术注》中，给出了证明三角形面积公式的出入相补法.如图所示，在 $△ A B C$ 中，分别取 $A B$ 、 $A C$ 的中点D、E，连接 $D E$ ，过点A作 $A F ⊥ D E$ ，垂足为F，将 $△ A B C$ 分割后拼接成矩形 $B C H G$ .若 $D E = 3 ， A F = 2$ ，则 $△ A B C$ 的面积是.

查看试题解析
15. 已知某一个数的平方根分别是 $n + 1$ 和 $n - 5$ ，则这个数为

查看试题解析
16. 如图，直线 $y = k x + b (k ＜ 0)$ 经过点 $A (3 ， 1)$ ，当 $k x + b < \frac{1}{3} x$ 时， $x$ 的取值范围为.

查看试题解析
17. 如图，从一个大正方形中截去面积为 $12$ 和 $3$ 的两个小正方形，若随机向大正方形内投一粒米，则米粒落在图中阴影部分的概率为

查看试题解析
18. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 x - 2 m + 5 = 0$ ，如果该方程的两个实数根都是符号相同的整数，则整数 $m$ 的值为

查看试题解析
19. 如图，已知 $Δ A B C$ 中 $∠ C = 90 ° ， A B = 6$ ， $C D$ 是斜边 $A B$ 的中线，将 $Δ A B C$ 绕着点 $A$ 旋转，使点 $B$ 、点 $C$ 分别落在点 $B^{'}$ 、点 $C^{'}$ 处，且点 $B^{'}$ 在射线 $C D$ 上，边 $A C'$ 与射线 $C D$ 交于点 $E$ .如果 $A E ： E C' = 3 ： 1 ，$ 那么线段 $C E$ 的长度是

查看试题解析

三、解答题

20.

(1)、计算： $| \sqrt{3} - 2 | + {(\frac{1}{3})}^{- 2} - {(1 - \sqrt{3})}^{0} + \sqrt{12}$

(2)、用配方法解方程： $x^{2} - 6 x - 2 = 0$

查看试题解析
21. 如图，已知在 $7 \times 7$ 的正方形网格中，每一个小正方形的边长为 $1 ，$ 点 $A 、 B$ 在格点上

(1)、请画出菱形ABCD，使得菱形ABCD的顶点都在格点上；（画出一个即可）

(2)、请根据你所画的菱形ABCD，完成下列填空：
①点A、C之间的距离为 ▲ ；
②线段AB、CD之间的距离为 ▲ ；

查看试题解析
22. 先化简，后求值： $(1 + \frac{1}{x - 2}) \div \frac{x^{2} - 2 x + 1}{x^{2} - 4}$ ，其中 $x = \sqrt{2} + 1$

查看试题解析
23. 2021年是中国共产党建党 $100$ 周年华诞.某市组织了“唱支歌儿给党听”合唱比赛.根据各参赛队的比赛成绩（ $10$ 分制，得分均为整数），整理并绘制了如下的条形统计图（不完整），已知有 $20 %$ 的参赛队比赛成绩为满分；

(1)、求参赛合唱队总数

(2)、若比赛成绩由高到低前 $40 %$ 的参赛队可以获奖.某一参赛队的比赛成绩为 $9$ 分，请你判断该合唱队能否获奖，并说明理由

(3)、甲、乙两个合唱队准备从“ $A 、 B 、 C$ ”三首歌曲中各自任选一首歌曲参加表演，且两个队表演歌曲各不相同.求事件“甲、乙两队所选两首歌曲中一定有 $A$ ”发生的概率.（树状图或列表法）

查看试题解析
24. 已知一次函数的图象经过点 $A (2 ， 3 ）$ 和点 $B （ 1 ， 0)$

(1)、请画出这个一次函数的图象；

(2)、求一次函数的解析式；

(3)、现以原点为位似中心，将线段 $A B$ 放大得到线段 $C D$ .如果点 $B$ 的对应点 $D$ 在 $x$ 轴上且 $O D = 2 ，$ 请你直接写出点 $A$ 的对应点 $C$ 的坐标.

查看试题解析
25. 已知在△ABC中，AC＝BC＝m，D是AB边上的一点，将∠B沿着过点D的直线折叠，使点B落在AC边的点P处（不与点A，C重合），折痕交BC边于点E.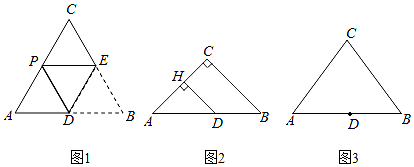

(1)、特例感知：如图1，若∠C＝60°，D是AB的中点，求证：AP＝ $\frac{1}{2}$ AC；

(2)、变式求异：如图2，若∠C＝90°，m＝ $6 \sqrt{2}$ ，AD＝7，过点D作DH⊥AC于点H，求DH和AP的长；

(3)、化归探究：如图3，若m＝10，AB＝12，且当AD＝a时，存在两次不同的折叠，使点B落在AC边上两个不同的位置，请直接写出a的取值范围.

查看试题解析
26. 德尔塔 $(D e l t a)$ 是一种全球流行的新冠病毒变异毒株，其传染性极强.某地有 $1$ 人感染了德尔塔，因为没有及时隔离治疗，经过两轮传染后，一共有 $144$ 人感染了德尔塔病毒，设每轮传染中平均一个人传染了 $x$ 个人；

(1)、用含 $x$ 的代数式表示：经过第一轮传染后，共有多少人感染了德尔塔病毒?

(2)、列方程求解：在每轮传染中，平均一个人传染了几个人?

(3)、如果按照这样的传染速度，经过三轮传染后，一共有多少人感染德尔塔病毒?

查看试题解析
27. 如图，已知在菱形 $A B C D$ 中， $∠ A B C$ 是锐角， $E$ 是 $B C$ 边上的动点，将射线 $A E$ 绕 $A$ 点按逆时针方向旋转，交直线 $C D$ 于点 $F$

(1)、当 $A E ⊥ B C ， ∠ E A F = ∠ A B C$ 时；
①根据条件，可判定 $Δ A B E ≅ Δ A D F$ ，请直接写出全等的判定依据；
②连结 $B D 、 E F$ ，若 $E F ： B D = 2 ： 5$ ，求 $S_{Δ A E F} ： S_{菱形 A B C D}$ 的值；

(2)、当 $∠ B A D = 2 ∠ E A F$ 时，延长 $B C$ 交射线 $A F$ 于点 $M$ ，延长 $D C$ 交射线 $A E$ 于点 $N ，$ 连结 $A C 、 M N ，$ 若 $A B = 4 ， A C = 2$ ，则当 $C E$ 为何值时， $Δ A M N$ 是等腰三角形，请直接写出结果

查看试题解析
28. 如图所示，在平面直角坐标系 $x O y$ 中，对于点 $P$ ，若点 $Q$ 满足条件：以线段 $P Q$ 为对角线的正方形，边均与某条坐标轴垂直，则称点 $Q$ 为点 $P$ 的“对角点”，该正方形为点 $P$ 的“对角正方形”；

(1)、已知点 $A$ 的坐标是 $（ 1 ， 3)$ ；
①在 $O (0 ， 0) 、 M （ 3 ， 3) 、 N （ 2 ， 2) 、 T (- 3 ， - 1)$ 这四个点中，请你判断：哪些点是点 $A$ 的“对角点”；
②若点 $A$ 的“对角正方形”面积是 $4$ ，请写出一个点 $A$ 的“对角点”的坐标；

(2)、若点 $B (1 ， 0)$ 的“对角点”在直线 $y = 2 x + 2$ 上，求点 $B$ 的“对角点”的坐标；

(3)、已知点 $C (m ， 0)$ ，如果直线 $y = 2 x + m$ 上存在点 $C$ 的“对角点”，使得点 $C$ 的“对角正方形”面积小于 $4 ，$ 请直接写出 $m$ 的取值范围

查看试题解析

排名	1	2	3	4	5	6	7	8	9	10
代表团	山东	广东	浙江	江苏	上海	湖北	福建	湖南	四川	辽宁
金牌数	$58$	$54$	$44$	$42$	$36$	$27$	$25$	$25$	$22$	$22$