四川省成都市东部新区2021-2022学年九年级上学期期中测试数学试题
试卷更新日期:2022-09-21 类型:期中考试
一、单选题
-
1. 将两个圆盘、一个茶叶桶、一个皮球和一个蒙古包模型按如图所示的方式摆放在一起,其主视图是( ).
 A、
A、 B、
B、 C、
C、 D、
D、 2. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定3. 甲、乙两位同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( )
2. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定3. 甲、乙两位同学在一次用频率去估计概率的实验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的实验可能是( ) A、掷一枚正六面体的骰子,出现1点的概率 B、一个袋子中有2个白球和1个红球,从中任取一个球,则取到红球的概率 C、抛一枚硬币,出现正面的概率 D、任意写一个整数,它能被2整除的概率4. 已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )A、 B、 C、 D、5. 如图,在中,点 , 分别在 , 上, , 则下列等式成立的是( )
A、掷一枚正六面体的骰子,出现1点的概率 B、一个袋子中有2个白球和1个红球,从中任取一个球,则取到红球的概率 C、抛一枚硬币,出现正面的概率 D、任意写一个整数,它能被2整除的概率4. 已知AB=2,点P是线段AB上的黄金分割点,且AP>BP,则AP的长为( )A、 B、 C、 D、5. 如图,在中,点 , 分别在 , 上, , 则下列等式成立的是( ) A、 B、 C、 D、6. 下列函数中,y是x的反比例函数的是( )A、x(y﹣1)=1 B、y= C、y=﹣x﹣1 D、y=7. 某种品牌运动服经过两次降价,每件零售价由460元将为215,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )A、460(1+x)2=215 B、460(1-x)2=215 C、460(1-2x)2=215 D、4 60(1-x2)=2158. 下列说法正确的是( )A、对角线互相垂直且相等的四边形是菱形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是平行四边形 D、对角线相等且互相平分的四边形是矩形9. 如图,在平面直角坐标系中,矩形OABC的顶点A,B在反比例函数 的图像上,纵坐标分别为1和3,则k的值为( )
A、 B、 C、 D、6. 下列函数中,y是x的反比例函数的是( )A、x(y﹣1)=1 B、y= C、y=﹣x﹣1 D、y=7. 某种品牌运动服经过两次降价,每件零售价由460元将为215,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )A、460(1+x)2=215 B、460(1-x)2=215 C、460(1-2x)2=215 D、4 60(1-x2)=2158. 下列说法正确的是( )A、对角线互相垂直且相等的四边形是菱形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是平行四边形 D、对角线相等且互相平分的四边形是矩形9. 如图,在平面直角坐标系中,矩形OABC的顶点A,B在反比例函数 的图像上,纵坐标分别为1和3,则k的值为( ) A、 B、 C、2 D、310. 如图, 是 的中位线, 是 的中点, 的延长线交 于点 ,若 的面积为 ,则 的值为
A、 B、 C、2 D、310. 如图, 是 的中位线, 是 的中点, 的延长线交 于点 ,若 的面积为 ,则 的值为 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 方程是关于的一元二次方程,则.12. 若 ,则 等于 .13. 已知反比例函数 , 当时,的值随x的增大而增大,则x的取值范围为.14.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=m.
 15. 已知 , 是方程的两个根,那么.16. 已知 , 则.17. 从1,2,3,4四个数中随机选取两个不同的数,分别记为 ,则关于x的一元二次方程 有实数解的概率为.18. 如图,已知函数的图象与轴、轴分别交于点、 , 与双曲线交于点、 , 若 , 则的值为.
15. 已知 , 是方程的两个根,那么.16. 已知 , 则.17. 从1,2,3,4四个数中随机选取两个不同的数,分别记为 ,则关于x的一元二次方程 有实数解的概率为.18. 如图,已知函数的图象与轴、轴分别交于点、 , 与双曲线交于点、 , 若 , 则的值为. 19. 如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ,∠EAF=45°,则AF的长为 .
19. 如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ,∠EAF=45°,则AF的长为 .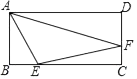
三、解答题
-
20.(1)、解方程:(2)、已知是关于的一元二次方程的一个根,求的值及方程的另一个根.21. 已知:关于的一元二次方程 , 当取何值时.(1)、方程有两个不相等的实数根?(2)、方程有两个相等的实数根?并求出这两个等根.22. 已知是坐标原点,、的坐标分别为、.
 (1)、画出绕点顺时针旋转后得到的△;(2)、在轴的左侧以为位似中心作的位似图形△ , 使新图与原图相似比为;(3)、求出△的面积.23. 初2019级为了解学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为 , , , 四个等级.请根据两幅统计图中的信息回答下列问题:
(1)、画出绕点顺时针旋转后得到的△;(2)、在轴的左侧以为位似中心作的位似图形△ , 使新图与原图相似比为;(3)、求出△的面积.23. 初2019级为了解学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为 , , , 四个等级.请根据两幅统计图中的信息回答下列问题: (1)、求测试结果为等级的学生数,并补全条形图;(2)、在扇形统计图中,试求等级对应的圆心角度数;(3)、若从体能为等级的名男生名女生中随机的抽取名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.24. 如图,一次函数与反比例函数的图象交于 , 两点.
(1)、求测试结果为等级的学生数,并补全条形图;(2)、在扇形统计图中,试求等级对应的圆心角度数;(3)、若从体能为等级的名男生名女生中随机的抽取名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.24. 如图,一次函数与反比例函数的图象交于 , 两点. (1)、求一次函数与反比例函数的表达式;(2)、根据所给条件,请直接写出不等式的解集;(3)、求.25. 在等腰中,. , 点、点分别在线段、线段上,射线与射线交于点 , 且 , 连接.(1)、如图1,当点为中点,求点到的距离;
(1)、求一次函数与反比例函数的表达式;(2)、根据所给条件,请直接写出不等式的解集;(3)、求.25. 在等腰中,. , 点、点分别在线段、线段上,射线与射线交于点 , 且 , 连接.(1)、如图1,当点为中点,求点到的距离; (2)、如图2,过点作的平行线交于点 , 过点作的平行线交于点 , 求证:;
(2)、如图2,过点作的平行线交于点 , 过点作的平行线交于点 , 求证:; (3)、设 , , 求与的函数关系式.26. 某水果批发商场经销一种高档水果,商场为了在中秋节和国庆节期间扩大销量,将售价从原来的每千克40元经两次调价后调至每千克32.4元.(1)、若该商场两次调次的降价率相同,求这个降价率;(2)、现在假期结束了,商场准备适当涨价,如果现在每千克盈利10元,每天可售出500千克,经市场调查发现,在进货不变的情况下,若每千克涨价1元,日销量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(3)、设 , , 求与的函数关系式.26. 某水果批发商场经销一种高档水果,商场为了在中秋节和国庆节期间扩大销量,将售价从原来的每千克40元经两次调价后调至每千克32.4元.(1)、若该商场两次调次的降价率相同,求这个降价率;(2)、现在假期结束了,商场准备适当涨价,如果现在每千克盈利10元,每天可售出500千克,经市场调查发现,在进货不变的情况下,若每千克涨价1元,日销量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?



