四川省绵阳市江油市2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-21 类型:期中考试
一、单选题
-
1. 下列计算错误的是( )A、 B、 C、 D、2. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )A、
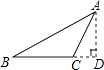 B、
B、 C、
C、 D、
D、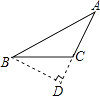 3. 若中, , 则一定是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、任意三角形4. 将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、900°5. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形 , 把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
3. 若中, , 则一定是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、任意三角形4. 将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、900°5. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形 , 把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )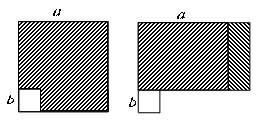 A、 B、 C、 D、6. 如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于 MN的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、 B、 C、 D、6. 如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于 MN的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
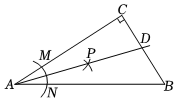
A、15 B、30 C、45 D、607. 下列命题:①三角形的一条中线把这个三角形的面积平分;②三角形的角平分线,中线,高线都在三角形的内部;③全等三角形面积相等,面积相等的三角形也全等;④三角形具有稳定性.其中真命题的个数是( )A、1 B、2 C、3 D、48. 如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
A、15 B、30 C、45 D、607. 下列命题:①三角形的一条中线把这个三角形的面积平分;②三角形的角平分线,中线,高线都在三角形的内部;③全等三角形面积相等,面积相等的三角形也全等;④三角形具有稳定性.其中真命题的个数是( )A、1 B、2 C、3 D、48. 如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )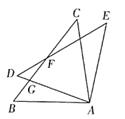 A、15° B、20° C、25° D、30°9. 如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A、15° B、20° C、25° D、30°9. 如图,∠A+∠B+∠C+∠D+∠E的度数为( )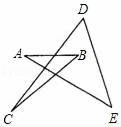 A、90° B、180° C、270° D、360°10. 如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠a+∠β的度数是( )
A、90° B、180° C、270° D、360°10. 如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠a+∠β的度数是( ) A、220° B、180° C、270° D、240°11. 已知a2-2a-1=0,则a4-2a3-2a+1等于( )A、0 B、1 C、2 D、312. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面正确的结论有( )
A、220° B、180° C、270° D、240°11. 已知a2-2a-1=0,则a4-2a3-2a+1等于( )A、0 B、1 C、2 D、312. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面正确的结论有( )①△ABE的面积=△BCE的面积;②AF=AG;③∠FAG=∠ACF④BH=CH
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图,AC与BD相交于点O , 且AB=CD , 请添加一个条件 , 使得△ABO≌△CDO .
 14. 若a、b、c为三角形的三边,且a、b满足 ,则第三边c的取值范围是 .15. 计算(-4a2+12a3b)÷(-4a2)的结果是.16. 如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时,则AP的长是 .
14. 若a、b、c为三角形的三边,且a、b满足 ,则第三边c的取值范围是 .15. 计算(-4a2+12a3b)÷(-4a2)的结果是.16. 如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时,则AP的长是 . 17. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为 .
17. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点C的坐标为 . 18. 如图,在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为.
18. 如图,在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为.
三、解答题
-
19.(1)、计算:(-2x2)3•(-xy)2÷(2x)(2)、已知一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.20.(1)、小明在计算一个多项式乘-2x2+x-1时,因看错运算符号,变成了加上-2x2+x-1,得到的结果为4x2-2x-1,那么正确的计算结果为多少?(2)、如图:AB=CD,AE⊥BC,DF⊥BC,垂足分别为E、F,CE=BF.求证:CD∥AB.
 21. 先简化,再求值.[(ab+1)(ab-2)-(2ab)2+2]÷(-ab),其中a=(-),b=-2021.22. 我国古代数学的许多发现都位居世界前列,其中“杨辉三角”(如图所示)就是一例这个三角形的构造法则为:
21. 先简化,再求值.[(ab+1)(ab-2)-(2ab)2+2]÷(-ab),其中a=(-),b=-2021.22. 我国古代数学的许多发现都位居世界前列,其中“杨辉三角”(如图所示)就是一例这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方(左右)两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律、例如,在三角形中第三行的三个数1、2、1,恰好对应(a+b)2=a2+2ab+b2展开式中各项的系数:第四行的四个数1、3、3、1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.
 (1)、根据上面的规律,(a+b)4展开式的各项系数中最大的数为;(2)、若(2x+1)2021=a1x2021+a2x2020+a3x2019+••••••+a2019x2+a2020x+1,求a1-a2+a3-……+a2020-1的值.
(1)、根据上面的规律,(a+b)4展开式的各项系数中最大的数为;(2)、若(2x+1)2021=a1x2021+a2x2020+a3x2019+••••••+a2019x2+a2020x+1,求a1-a2+a3-……+a2020-1的值.

