四川省绵阳市2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下面国产汽车品牌标志中，是轴对称图形的有（）个．

A、1 B、2 C、3 D、4

查看试题解析
2. 若三角形的两边长分别为6，8，则第三边长可以是（）

A、1 B、2 C、10 D、15

查看试题解析
3. 如图， $∠ C = ∠ F$ =90°，下列条件中，不能判定 $△ A C B$ 与 $△ D F E$ 全等的是（）

A、 $∠ A = ∠ D$ ， $A B = D E$ B、 $A C = D F$ ， $B C = E F$ C、 $A B = D E$ ， $B C = E F$ D、 $∠ A = ∠ D$ ， $∠ B = ∠ E$

查看试题解析
4. 下列运算正确的是（）

A、a³＋a³＝2a⁶ B、a⁶•a³＝a¹⁸ C、a³•a³＝2a³ D、（﹣2a²）³＝﹣8a⁶

查看试题解析
5. 下列说法：
①钝角三角形有两条高在三角形内部；②三角形的三条高都在三角形内部； ③三角形的三条高的交点不在三角形内部，就在三角形外部；④锐角三角形三条高的交点一定在三角形内部，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，五边形ABCDE是正五边形，若l₁∥l₂ ，则∠1﹣∠2的值是（）

A、108° B、36° C、72° D、144°

查看试题解析
7. 一个三角形其中一个外角的补角等于与它不相邻的两个内角的差，则这个三角形一定是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形

查看试题解析
8. 如图，△ABC是边长为2的等边三角形，点P在AB上，过点P作PE⊥AC ，垂足为E ，延长BC到点Q ，使CQ＝PA ，连接PQ交AC于点D ，则DE的长为（）

A、0.5 B、0.9 C、1 D、1.25

查看试题解析
9. 在 $△ A B C$ 中，已知 $A C ： B C ： A B = 5 ： 12 ： 13$ ，AD是 $△ A B C$ 的角平分线， $D E ⊥ A B$ 于点E.若 $△ A B C$ 的面积为S，则 $△ A C D$ 的面积为（）

A、 $\frac{1}{4} S$ B、 $\frac{5}{18} S$ C、 $\frac{6}{25} S$ D、 $\frac{7}{25} S$

查看试题解析
10. 如图，在△ABC中，AB＝BC，∠A＝36°，AB的垂直平分线DE交AB于点D，交AC于点E，若AB＝10，则CE的长为（）

A、5 B、8 C、10 D、10 $\sqrt{2}$

查看试题解析
11. 若 $\underset{k 个 3^{3}}{\underset{︸}{3^{3} + 3^{3} + 3^{3} + \cdot \cdot \cdot + 3^{3}}} = 3^{m}$ （ $k > 1$ ， $k$ ， $m$ 都为正整数），则 $m$ 的最小值为（）

A、3 B、4 C、6 D、9

查看试题解析
12. 如图，在△ABC中，∠BAC和∠ABC的平分线AE，BF相交于点O，AE交BC于E，BF交AC于F，过点O作OD⊥BC于D，下列四个结论：①∠AOB＝90°+ $\frac{1}{2}$ ∠C；②当∠C＝60°时，AF+BE＝AB； ③若OD＝a，AB+BC+CA＝2b，则S_△ABC＝ab.其中正确的是（）

A、①② B、②③ C、①②③ D、①③

查看试题解析
13. 如图，△ABC中，∠ACB＝90°，∠A＝30°，将△ABC绕C点按逆时针方向旋转 $α$ 角(0°＜ $α$ ＜90°)得到△DEC，设CD交AB于点F，连接AD，当旋转角 $α$ 度数为____，△ADF是等腰三角形．

A、20° B、40° C、10° D、20°或40°

查看试题解析

二、填空题

14. 一个多边形的内角和是它的外角和的4.5倍，这个多边形的边数是．

查看试题解析
15. 已知2a＝3，2b＝5，则2²a＋2a^＋b＝．

查看试题解析
16. 在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A的坐标是（ $\sqrt{3} ， \sqrt{2}$ ），则经过第2019次变换后所得的点A的坐标是．

查看试题解析
17. 如图，将一个正八边形与一个正六边形如图放置，顶点A、B、C、D四点共线，E为公共顶点．则∠FEG＝．

查看试题解析
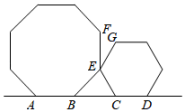18. 如图，四边形ABCD中，∠C＝58°，∠B＝∠D＝90°，E、F分别是BC、DC上的点，当△AEF的周长最小时，∠EAF的度数为．

查看试题解析

三、解答题

19. 2（x³）²∙x³-（3x³）³+（5x）²∙x⁷

查看试题解析
20. 如图，在边长为1的小正方形网格中，点A，B，C均落在格点上．

⑴求△ABC的面积？

⑵画出△ABC关于直线l的轴对称图形△A₁B₁C₁ ．

⑶在直线l上有一点P使PC+PB最小，请画出点P．

查看试题解析
21. 若关于x，y的二元一次方程组 ${\begin{array}{l} 3 x - y = 2 a - 5 \\ x + 2 y = 3 a + 3 \end{array}$ 的解都是正数．

(1)、求a的取值范围；

(2)、若此方程组的解是一个等腰三角形的一条腰和底边的长，且这个等腰三角形的周长为12，求a的值．

查看试题解析
22. 如图，在△ABC中，AB=AC，DE垂直平分AB，交边AB于点D，交边AC于点E，BF垂直平分CE，交AC于点F，连接BE．

(1)、请直接写出∠A与∠C的关系为；

(2)、求∠A的度数．

查看试题解析
23. 如图，在△ABC中，∠C＝90°，∠A＝30°，AB＝4cm，动点P、Q同时从A、B两点出发，分别在AB、BC边上匀速移动，它们的速度分别为VP＝2cm/s，VQ＝1cm/s，当点P到达点B时，P、Q两点同时停止运动，设点P的运动时间为ts．

(1)、当t为何值时，△PBQ为等边三角形？

(2)、当t为何值时，△PBQ为直角三角形？

查看试题解析
24. 如图，AD为△ABC的角平分线，E为BC的中点，EF∥AD交BA的延长线于F，交AC于G．

(1)、求证：AF＝AG；

(2)、求证：BF＝CG；

(3)、直接写出 $\frac{A B + A C}{C G}$ 的值．

查看试题解析