四川省德阳广汉市2021-2022学年八年级上学期期中考试数学试题
试卷更新日期:2022-09-21 类型:期中考试
一、单选题
-
1. 以下列各组线段为边,能组成三角形的是( )A、2cm,3cm,5cm B、3cm,3cm,6cm C、2cm,5cm,8cm D、4cm,5cm,6cm2. 下列计算正确的是( )A、 B、 C、 D、3. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、
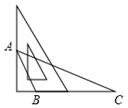 B、
B、 C、
C、 D、
D、 4. 如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则可增加的条件是( )
4. 如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则可增加的条件是( ) A、∠ABE=∠DBE B、∠A=∠D C、∠E=∠C D、∠1=∠25. 如图,如果△ABC≌△FED,那么下列结论错误的是( )
A、∠ABE=∠DBE B、∠A=∠D C、∠E=∠C D、∠1=∠25. 如图,如果△ABC≌△FED,那么下列结论错误的是( )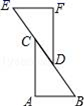 A、EC=BD B、EF∥AB C、DF=BD D、AC∥FD6. 如图,将两根钢条 , 的中点O连在一起,使 , 可绕点O自由转动,就做成了一个测量工件,则 的长等于内槽宽 ,那么判定 的理由是( )
A、EC=BD B、EF∥AB C、DF=BD D、AC∥FD6. 如图,将两根钢条 , 的中点O连在一起,使 , 可绕点O自由转动,就做成了一个测量工件,则 的长等于内槽宽 ,那么判定 的理由是( )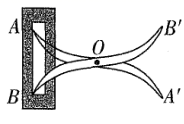 A、边角边 B、角边角 C、边边边 D、角角边7. 如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2的度数为( )
A、边角边 B、角边角 C、边边边 D、角角边7. 如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=120°,则∠1+∠2的度数为( )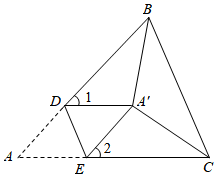 A、90° B、100° C、110° D、120°8. 如图, , , 于 点, 于 点, , , 则 的长为 ( )
A、90° B、100° C、110° D、120°8. 如图, , , 于 点, 于 点, , , 则 的长为 ( ) A、 B、 C、 D、9. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2 , AB=20cm,AC=8cm,则DE的长是( )
A、 B、 C、 D、9. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2 , AB=20cm,AC=8cm,则DE的长是( )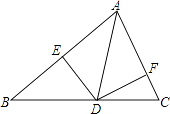 A、4cm B、3cm C、2cm D、1cm10. 如图,△ABC的面积为10,AD为BC边上的中线,E为AD上任意一点,连接BE、CE,图中阴影部分的面积为( )
A、4cm B、3cm C、2cm D、1cm10. 如图,△ABC的面积为10,AD为BC边上的中线,E为AD上任意一点,连接BE、CE,图中阴影部分的面积为( )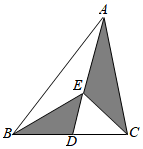 A、4 B、5 C、6 D、811. 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )
A、4 B、5 C、6 D、811. 如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是( )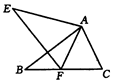 A、1个 B、2个 C、3个 D、4个12. 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连接BE,且BE边平分∠ABC,则以下命题不正确的个数是①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD;⑤BC=CE.( )
A、1个 B、2个 C、3个 D、4个12. 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连接BE,且BE边平分∠ABC,则以下命题不正确的个数是①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=S四边形ABCD;⑤BC=CE.( ) A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
13. 计算:22018×0.52018= .14. (4a2﹣8a)÷2a= .15. 如图,已知BD=CE,∠B=∠C,若AB=8,AD=3,则DC=.
 16. 如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是.
16. 如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是. 17. 如图,小明从A点出发前进10m,向右转20°,再前进10m,又向右转20°,…这样一直走下去,他第一次回到出发点A时,一共走了m.
17. 如图,小明从A点出发前进10m,向右转20°,再前进10m,又向右转20°,…这样一直走下去,他第一次回到出发点A时,一共走了m. 18. 已知方格纸中的每个小方格是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,在小方格的顶点上确定一点C,连接AB、AC、BC,使△ABC的面积为3个平方单位.则这样的点C共有 个.
18. 已知方格纸中的每个小方格是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示,在小方格的顶点上确定一点C,连接AB、AC、BC,使△ABC的面积为3个平方单位.则这样的点C共有 个.
三、解答题
-
19.(1)、先化简,再求值: , 其中a=4.(2)、若a,b,c分别为三角形的三边,化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a+b|20. 如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.
 (1)、求证:△ABC≌△DFE;(2)、若BF=14,EC=4,求BC的长.21. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)、求证:△ABC≌△DFE;(2)、若BF=14,EC=4,求BC的长.21. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC. (1)、请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)、证明:DC⊥BE .22. 如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.
(1)、请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)、证明:DC⊥BE .22. 如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE. (1)、求证:点E到DA,DC的距离相等;(2)、求∠DEB的度数.23. 如图1所示,等腰直角三角形 中, , ,直线 经过点 , 于点 , 于点 .
(1)、求证:点E到DA,DC的距离相等;(2)、求∠DEB的度数.23. 如图1所示,等腰直角三角形 中, , ,直线 经过点 , 于点 , 于点 . (1)、求证: ;(2)、求证: ;(3)、当直线 运动到如图2所示位置时,其余条件不变,直接写出线段 、 、 之间的数量关系.
(1)、求证: ;(2)、求证: ;(3)、当直线 运动到如图2所示位置时,其余条件不变,直接写出线段 、 、 之间的数量关系. 24. 在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
24. 在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE. (1)、如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE=;(2)、设∠BAC=α,∠DCE=β.
(1)、如图,当点D在BC延长线上移动时,若∠BAC=25°,则∠DCE=;(2)、设∠BAC=α,∠DCE=β.①当点D在BC延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C两点重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.
25. 如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.如果点P在线段BC上以1cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.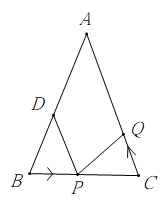 (1)、若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(2)、若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(3)、若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
(1)、若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(2)、若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(3)、若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?