四川省成都市东部新区2021-2022学年八年级上学期期中测试数学试题
试卷更新日期:2022-09-21 类型:期中考试
一、单选题
-
1. 下列实数中是无理数的是( )A、 B、0.212121 C、 D、﹣2. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点 .“馬”位于点 ,则“兵”位于点( )
 A、 B、 C、 D、3. 下列各数中,以 , , 为边的三角形不是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列计算正确的是( )A、 B、 C、 D、5. 使二次根式有意义的的取值范围是( )A、 B、 C、 D、6. 2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平,自1月底抗击“新冠病毒”以来,消毒液霱求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示2020年初至脱销期间,该厂库存量y(吨)与时间(天)之间函数关系的大致图象是( )A、
A、 B、 C、 D、3. 下列各数中,以 , , 为边的三角形不是直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列计算正确的是( )A、 B、 C、 D、5. 使二次根式有意义的的取值范围是( )A、 B、 C、 D、6. 2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平,自1月底抗击“新冠病毒”以来,消毒液霱求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示2020年初至脱销期间,该厂库存量y(吨)与时间(天)之间函数关系的大致图象是( )A、 B、
B、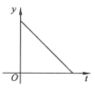 C、
C、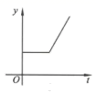 D、
D、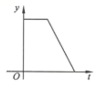 7. 若直角三角形两条直角边的边长分别为6和8,则斜边上的高是( )A、5 B、10 C、 D、8. 如图,圆柱的高为8cm,底面半径为 cm,一只蚂蚁从点A沿圆柱外壁爬到点B处吃食,要爬行的最短路程是( )
7. 若直角三角形两条直角边的边长分别为6和8,则斜边上的高是( )A、5 B、10 C、 D、8. 如图,圆柱的高为8cm,底面半径为 cm,一只蚂蚁从点A沿圆柱外壁爬到点B处吃食,要爬行的最短路程是( )
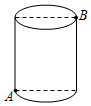 A、6cm B、8cm C、10cm D、12cm9. 下列图象中,y不是x的函数的是A、
A、6cm B、8cm C、10cm D、12cm9. 下列图象中,y不是x的函数的是A、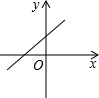 B、
B、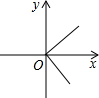 C、
C、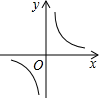 D、
D、 10. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
10. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( ) A、9 B、6 C、4 D、3
A、9 B、6 C、4 D、3二、填空题
-
11. 的平方根是 .12. 若点在第三象限,则应在第象限.13. 若一次函数与图象的交点纵坐标为 , 则的值为.14. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9cm,则正方形A,B,C,D的面积的和是cm2
 15. 已知 , 则.16. 如果函数的自变量的取值范围是 , 相应的函数值的范围是 , 求此函数的解析式是.17. 如图,在中, , 是的中点, , 交的延长线于点.若 , , 则的长为.
15. 已知 , 则.16. 如果函数的自变量的取值范围是 , 相应的函数值的范围是 , 求此函数的解析式是.17. 如图,在中, , 是的中点, , 交的延长线于点.若 , , 则的长为. 18. 如图,、都是等腰直角三角形, , , , .将绕点逆时针方向旋转后得 , 当点恰好落在线段上时,则.
18. 如图,、都是等腰直角三角形, , , , .将绕点逆时针方向旋转后得 , 当点恰好落在线段上时,则. 19. 直线与轴、轴分别交于点 , , 是轴上一点,若将沿折叠,点恰好落在轴上,则点的坐标为.
19. 直线与轴、轴分别交于点 , , 是轴上一点,若将沿折叠,点恰好落在轴上,则点的坐标为.
三、解答题
-
20. 计算题(1)、计算:(2)、计算:(3)、计算:(4)、解方程:21. 先化简,再求值:(2a﹣3)(a+1)﹣a(a﹣3),其中a=﹣1.22. 如图,有一块菜地,已知AB=4m,BC=3m,AB⊥BC,AD=m,CD=10m,求这块地的面积.
 23. 如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中,A(﹣4,5),B(﹣2,1),C(﹣1,3).
23. 如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中,A(﹣4,5),B(﹣2,1),C(﹣1,3). (1)、作出△ABC关于y轴对称的△A1B1C1;(2)、写出△A1B1C1的各顶点的坐标;(3)、求△ABC的面积.24. 如图,是将长方形纸片沿对角线折叠后得到的.
(1)、作出△ABC关于y轴对称的△A1B1C1;(2)、写出△A1B1C1的各顶点的坐标;(3)、求△ABC的面积.24. 如图,是将长方形纸片沿对角线折叠后得到的. (1)、试判断的形状,并说明理由;(2)、若 , , 求的面积.25. 如图1,在 中, ,点D,E分别在边 上,且 ,连接 .现将 绕点A顺时针方向旋转,旋转角为 ,如图2,连接 .
(1)、试判断的形状,并说明理由;(2)、若 , , 求的面积.25. 如图1,在 中, ,点D,E分别在边 上,且 ,连接 .现将 绕点A顺时针方向旋转,旋转角为 ,如图2,连接 .
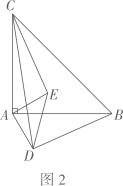
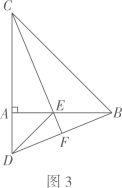 (1)、当 时,求证: ;(2)、如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;(3)、在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.26. 已知x= , y=(1)、求x2+xy+y2.(2)、若x的小数部分为a,y的整数部分为b,求ax+by的平方根.27. 如图,在△ABC中,∠B=45°, , 等腰直角△DAE中,∠DAE=90°,且点D是边BC上一点.
(1)、当 时,求证: ;(2)、如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;(3)、在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.26. 已知x= , y=(1)、求x2+xy+y2.(2)、若x的小数部分为a,y的整数部分为b,求ax+by的平方根.27. 如图,在△ABC中,∠B=45°, , 等腰直角△DAE中,∠DAE=90°,且点D是边BC上一点. (1)、求的长;(2)、如图1,当点恰在上时,求点到的距离;(3)、如图2,当点从点向点运动时,求点到的距离的最大值.28. 建立模型:
(1)、求的长;(2)、如图1,当点恰在上时,求点到的距离;(3)、如图2,当点从点向点运动时,求点到的距离的最大值.28. 建立模型:

 (1)、如图 1,已知 , , , 顶点在直线 上.操作:过点作于点 , 过点作于点 , 求证.
(1)、如图 1,已知 , , , 顶点在直线 上.操作:过点作于点 , 过点作于点 , 求证.模型应用:
(2)、如图2,在直角坐标系中,直线:与轴交于点 , 与轴交于点 , 将直线绕着点顺时针旋转得到 , 求的函数表达式.(3)、如图3,在直角坐标系中,点 , 作轴于点 , 作于点 , 是线段上的一个动点,点位于第一象限内.问点、、能否构成以点为直角顶点的等腰直角三角形,若能,请求出此时点的坐标;若不能,请说明理由.