江苏省镇江市2022年中考数学试卷
试卷更新日期:2022-09-20 类型:中考真卷
一、填空题
-
1. 计算:3+(﹣2)=.2. 使有意义的x的取值范围是.3. 分解因式: .4. 一副三角板如图放置, , , , 则 .
 5. 已知关于的一元二次方程有两个相等的实数根,则 .6. 某班40名学生体重的频数分布直方图(不完整)如图所示,组距为 .
5. 已知关于的一元二次方程有两个相等的实数根,则 .6. 某班40名学生体重的频数分布直方图(不完整)如图所示,组距为 .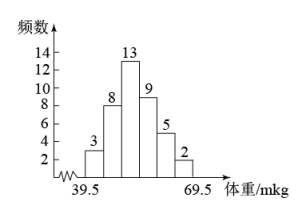 7. 如图,在和中, , 、、分别为、、的中点,若 , 则 .
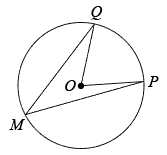
7. 如图,在和中, , 、、分别为、、的中点,若 , 则 . 8. 《九章算术》中记载,战国时期的铜衡杆,其形式既不同于天平衡杆,也异于称杆衡杆正中有拱肩提纽和穿线孔,一面刻有贯通上、下的十等分线.用该衡杆称物,可以把被称物与砝码放在提纽两边不同位置的刻线上,这样,用同一个砝码就可以称出大于它一倍或几倍重量的物体.图为铜衡杆的使用示意图,此时被称物重量是砝码重量的倍.
8. 《九章算术》中记载,战国时期的铜衡杆,其形式既不同于天平衡杆,也异于称杆衡杆正中有拱肩提纽和穿线孔,一面刻有贯通上、下的十等分线.用该衡杆称物,可以把被称物与砝码放在提纽两边不同位置的刻线上,这样,用同一个砝码就可以称出大于它一倍或几倍重量的物体.图为铜衡杆的使用示意图,此时被称物重量是砝码重量的倍.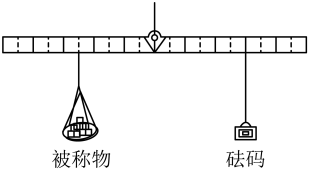 9. 反比例函数的图象经过、两点,当时, , 写出符合条件的的值(答案不唯一,写出一个即可).10. “五月天山雪,无花只有寒”,反映出地形对气温的影响.大致海拔每升高100米,气温约下降 . 有一座海拔为2350米的山,在这座山上海拔为350米的地方测得气温是 , 则此时山顶的气温约为 .11. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .
9. 反比例函数的图象经过、两点,当时, , 写出符合条件的的值(答案不唯一,写出一个即可).10. “五月天山雪,无花只有寒”,反映出地形对气温的影响.大致海拔每升高100米,气温约下降 . 有一座海拔为2350米的山,在这座山上海拔为350米的地方测得气温是 , 则此时山顶的气温约为 .11. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .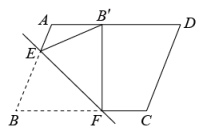 12. 从2021、2022、2023、2024、2025这五个数中任意抽取3个数.抽到中位数是2022的3个数的概率等于 .
12. 从2021、2022、2023、2024、2025这五个数中任意抽取3个数.抽到中位数是2022的3个数的概率等于 .二、单选题
-
13. 下列运算中,结果正确的是( )A、 B、 C、 D、14. 如图,数轴上的点A和点B分别在原点的左侧和右侧,点A、B对应的实数分别是a、b,下列结论一定成立的是( )
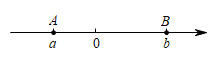 A、 B、 C、 D、15. “珍爱地球,人与自然和谐共生”是今年世界地球日的主题,旨在倡导公众保护自然资源.全市现有自然湿地28700公顷,人工湿地13100公顷,这两类湿地共有( )A、公顷 B、公顷 C、公顷 D、公顷16. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( )
A、 B、 C、 D、15. “珍爱地球,人与自然和谐共生”是今年世界地球日的主题,旨在倡导公众保护自然资源.全市现有自然湿地28700公顷,人工湿地13100公顷,这两类湿地共有( )A、公顷 B、公顷 C、公顷 D、公顷16. 如图,点、、、在网格中小正方形的顶点处,与相交于点 , 小正方形的边长为1,则的长等于( ) A、2 B、 C、 D、17. 第1组数据为:0、0、0、1、1、1,第2组数据为:、 , 其中、是正整数.下列结论:①当时,两组数据的平均数相等;②当时,第1组数据的平均数小于第2组数据的平均数;③当时,第1组数据的中位数小于第2组数据的中位数;④当时,第2组数据的方差小于第1组数据的方差.其中正确的是( )A、①② B、①③ C、①④ D、③④18. 如图,在等腰中, , BC= , 同时与边的延长线、射线相切,的半径为3.将绕点按顺时针方向旋转 , 、的对应点分别为、 , 在旋转的过程中边所在直线与相切的次数为( )
A、2 B、 C、 D、17. 第1组数据为:0、0、0、1、1、1,第2组数据为:、 , 其中、是正整数.下列结论:①当时,两组数据的平均数相等;②当时,第1组数据的平均数小于第2组数据的平均数;③当时,第1组数据的中位数小于第2组数据的中位数;④当时,第2组数据的方差小于第1组数据的方差.其中正确的是( )A、①② B、①③ C、①④ D、③④18. 如图,在等腰中, , BC= , 同时与边的延长线、射线相切,的半径为3.将绕点按顺时针方向旋转 , 、的对应点分别为、 , 在旋转的过程中边所在直线与相切的次数为( )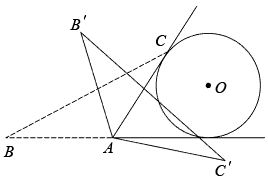 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4三、解答题
-
19.(1)、计算:;(2)、化简: .20.(1)、解方程:;(2)、解不等式组: .21. 一只不透明的袋子中装有2个白球、1个红球,这些球除颜色外都相同.(1)、搅匀后从中任意摸出一个球,摸到红球的概率等于;(2)、搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出一个球.用列表或画树状图的方法,求2次都摸到红球的概率.22. 某地交警在一个路口对某个时段来往的车辆的车速进行监测,统计数据如下表:
车速()
40
41
42
43
44
45
频数
6
8
15
3
2
其中车速为40、43(单位:)的车辆数分别占监测的车辆总数的12%、32%.
(1)、求出表格中的值;(2)、如果一辆汽车行驶的车速不超过的10%,就认定这辆车是安全行驶.若一年内在该时段通过此路口的车辆有20000辆,试估计其中安全行驶的车辆数.23. 某公司专业生产某种产品,6月初(当月月历如图)接到一份求购5000件该产品的订单,要求本月底完成,7月1日按期交货.日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
经盘点目前公司已有该产品库存2855件,补充原材料后,从本月7日开始生产剩余数量的该产品,已知该公司除周六、周日正常休息外,每天的生产量相同.但因受高温天气影响,从本月10日开始,每天的生产量比原来减少了25件,截止到17日生产结束,库存总量达3830件.如果按照10日开始的生产速度继续生产该产品,能否按期完成订单?请说明理由.如果不能,请你给该公司生产部门提出一个合理的建议,以确保能按期交货.
24. 如图,一次函数与反比例函数的图象交于点 , 与轴交于点 .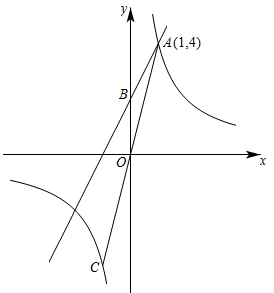 (1)、 , ;(2)、连接并延长 , 与反比例函数的图象交于点 , 点在轴上,若以、、为顶点的三角形与相似,求点的坐标.25. 如图1是一张圆凳的造型,已知这张圆凳的上、下底面圆的直径都是 , 高为 . 它被平行于上、下底面的平面所截得的横截面都是圆.小明画出了它的主视图,是由上、下底面圆的直径、以及、组成的轴对称图形,直线为对称轴,点、分别是、的中点,如图2,他又画出了所在的扇形并度量出扇形的圆心角 , 发现并证明了点在上.请你继续完成长的计算.
(1)、 , ;(2)、连接并延长 , 与反比例函数的图象交于点 , 点在轴上,若以、、为顶点的三角形与相似,求点的坐标.25. 如图1是一张圆凳的造型,已知这张圆凳的上、下底面圆的直径都是 , 高为 . 它被平行于上、下底面的平面所截得的横截面都是圆.小明画出了它的主视图,是由上、下底面圆的直径、以及、组成的轴对称图形,直线为对称轴,点、分别是、的中点,如图2,他又画出了所在的扇形并度量出扇形的圆心角 , 发现并证明了点在上.请你继续完成长的计算.参考数据: , , , , , .
 26. 已知,点、、、分别在正方形的边、、、上.
26. 已知,点、、、分别在正方形的边、、、上.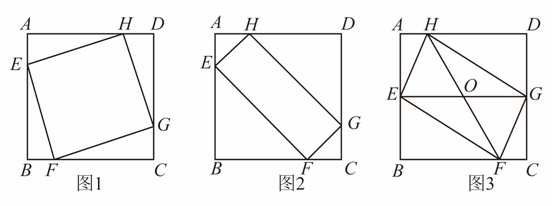 (1)、如图1,当四边形是正方形时,求证:;(2)、如图2,已知 , , 当、的大小有关系时,四边形是矩形;(3)、如图3, , 、相交于点 , , 已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.27. 一次函数的图象与轴交于点 , 二次函数的图象经过点、原点和一次函数图象上的点 .
(1)、如图1,当四边形是正方形时,求证:;(2)、如图2,已知 , , 当、的大小有关系时,四边形是矩形;(3)、如图3, , 、相交于点 , , 已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.27. 一次函数的图象与轴交于点 , 二次函数的图象经过点、原点和一次函数图象上的点 . (1)、求这个二次函数的表达式;(2)、如图1,一次函数与二次函数的图象交于点、(),过点作直线轴于点 , 过点作直线轴,过点作于点 .
(1)、求这个二次函数的表达式;(2)、如图1,一次函数与二次函数的图象交于点、(),过点作直线轴于点 , 过点作直线轴,过点作于点 .①▲ , ▲ (分别用含的代数式表示);
②证明:;
(3)、如图2,二次函数的图像是由二次函数的图像平移后得到的,且与一次函数的图像交于点、(点在点的左侧),过点作直线轴,过点作直线轴,设平移后点、的对应点分别为、 , 过点作于点 , 过点作于点 .①与相等吗?请说明你的理由;
②若 , 求的值.
28. 操作探究题(1)、已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.操作:如图1,分别将半圆的圆心角(取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);

交流:当时,可以仅用圆规将半圆的圆心角所对的弧三等分吗?
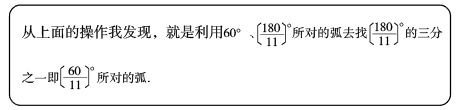
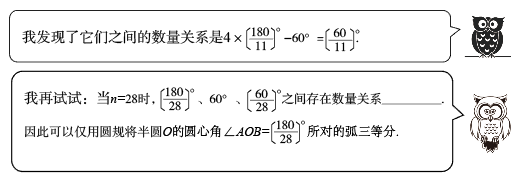
探究:你认为当满足什么条件时,就可以仅用圆规将半圆的圆心角所对的弧三等分?说说你的理由.
(2)、如图2,的圆周角 . 为了将这个圆的圆周14等分,请作出它的一条14等分弧(要求:仅用圆规作图,不写作法,保留作图痕迹).