广西南宁四十七中2022-2023学年九年级上学期开学数学试卷
试卷更新日期:2022-09-20 类型:开学考试
一、选择题(本大题共12小题,共36分。)
-
1. 下列图形分别是中国铁路、中国交建、中国航天、中国公路的标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知点的坐标是 , 则点关于原点的对称点的坐标是( )A、 B、 C、 D、3. 信息技术课上,在老师的指导下,小好同学训练打字速度(字/min),数据整理如下:15,17,23,15,17,17,19,21,21,18,对于这组数据,下列说法正确的是( )A、众数是17 B、众数是15 C、中位数是17 D、中位数是184. 下列命题中,正确的个数是( )
2. 已知点的坐标是 , 则点关于原点的对称点的坐标是( )A、 B、 C、 D、3. 信息技术课上,在老师的指导下,小好同学训练打字速度(字/min),数据整理如下:15,17,23,15,17,17,19,21,21,18,对于这组数据,下列说法正确的是( )A、众数是17 B、众数是15 C、中位数是17 D、中位数是184. 下列命题中,正确的个数是( )①直径是弦,弦是直径;②弦是圆上的两点间的部分;③半圆是弧,但弧不一定是半圆;④直径相等的两个圆是等圆;⑤等于半径两倍的线段是直径.
A、2个 B、3个 C、4个 D、5个5. 如图,在 中,点D,点E分别是AB,AC的中点,点F是DE上一点,且 ,若 , ,则DF的长为( ) A、2 B、3 C、4 D、56. 如图,在中, , , 将绕点按顺时针方向旋转后得到 , 此时点在边上,则旋转角的大小为( )
A、2 B、3 C、4 D、56. 如图,在中, , , 将绕点按顺时针方向旋转后得到 , 此时点在边上,则旋转角的大小为( ) A、 B、 C、 D、7. 如图:为内一点,平分 , , , 若 , , 则的长为( )
A、 B、 C、 D、7. 如图:为内一点,平分 , , , 若 , , 则的长为( ) A、5 B、4 C、3 D、28. 一个等腰三角形的两条边长分别是方程 的两根,则该等腰三角形的周长是( )A、12 B、9 C、13 D、12或99. 在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )A、
A、5 B、4 C、3 D、28. 一个等腰三角形的两条边长分别是方程 的两根,则该等腰三角形的周长是( )A、12 B、9 C、13 D、12或99. 在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )A、 B、
B、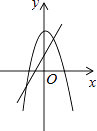 C、
C、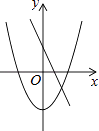 D、
D、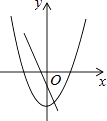 10. 二次函数 的图象 如图所示,则该函数在所给自变量的取值范围内,函数值y的取值范围是( )
10. 二次函数 的图象 如图所示,则该函数在所给自变量的取值范围内,函数值y的取值范围是( ) A、 B、 C、 D、11. 将4个数 , , , 排成2行、2列,两边各加一条竖线,记成 , 并规定例如 , 则的根的情况为( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根12. 二次函数的图象如图所示,下列结论:;②若为任意实数,则;;;若 , 且 , 则其中正确的个数为( )
A、 B、 C、 D、11. 将4个数 , , , 排成2行、2列,两边各加一条竖线,记成 , 并规定例如 , 则的根的情况为( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根12. 二次函数的图象如图所示,下列结论:;②若为任意实数,则;;;若 , 且 , 则其中正确的个数为( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题(本大题共6小题,共12分)
-
13. 因式分解: .14. 已知关于的方程的两实数根互为相反数,则 .15. 飞机着陆后滑行的距离单位:米关于滑行的时间单位:秒的函数解析式是 , 则飞机停下前最后10秒滑行的距离是米.16. 如图,二次函数 与一次函数 的图象相交于点 , ,则使 成立的x的取值范围是 .
 17. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,点A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=3.运动过程中点D到点O的最大距离是 .
17. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,点A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=3.运动过程中点D到点O的最大距离是 . 18. 如图,点在直线上,过点作轴交直线于点 , 以点为直角顶点,为直角边,在的右侧作等腰直角 , 再过点作轴交直线和直线于 , 两点,再以点为直角顶点,为直角边在的右侧作等腰直角 , , 按此规律进行下去,则等腰直角的边长为用含正整数的代数式表示
18. 如图,点在直线上,过点作轴交直线于点 , 以点为直角顶点,为直角边,在的右侧作等腰直角 , 再过点作轴交直线和直线于 , 两点,再以点为直角顶点,为直角边在的右侧作等腰直角 , , 按此规律进行下去,则等腰直角的边长为用含正整数的代数式表示
三、计算题(本大题共2小题,共12分)
-
19. 计算: .20. 解方程:
四、解答题(本大题共6小题,共60分。)
-
21. 如图,在中, , 是的一个外角.
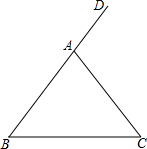
⑴作的平分线;
⑵作线段的垂直平分线,与交于点 , 与边交于点 , 连接 , .
⑶判断四边形的形状并加以证明.
22. “聚焦双减,落实五项管理”,为了解双减政策实施以来同学们的学习状态,某校志愿者调研了七,八年级部分同学完成作业的时间情况.从七,八年级中各抽取20名同学作业完成时间数据(单位:分钟)进行整理和分析,共分为四个时段(x表示作业完成时间,取整数);;;; , 完成作业不超过80分钟为时间管理优秀,下面给出部分信息:
七年级抽取20名同学的完成作业时间:55,58,60,65,64,66,60,60,78﹐
78,70,75,75,78,78,80,82,85,85,88.

八年级抽取20名同学中完成作业时间在时段的所有数据为:72,75,74,76,75,75,78,75.
七,八年级抽取的同学完成作业时间统计表:
年级
平均数
中位数
众数
七年级
72
75
八年级
75
75
根据以上信息,解答下列问题:
(1)、填空: ▲ , ▲ , 并补全统计图;(2)、根据以上数据分析,双减政策背景的作业时间管理中,哪个年级落实得更好?请说明理由;(写出一条即可)(3)、该校七年级有900人,八年级有700人,估计七,八年级时间管理优秀的共有多少人?23. 如果关于的一元二次方程有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为 , 则另一个根为 , 因此 , 所以有;我们记“”即时,方程为倍根方程;下面我们根据此结论来解决问题:(1)、方程;方程这两个方程中,是倍根方程的是填序号即可;(2)、若是倍根方程,求的值;(3)、关于的一元二次方程是倍根方程,且点在一次函数的图象上,求此倍根方程的表达式.24. 2022年北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民的喜爱.某特许零售店“冰墩墩”的销售日益火爆.每个纪念品进价40元,规定销售单价不低于44元,且不高于52元.销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每上涨1元,每天销量减少10个.现商家决定提价销售,设每天销售量为y个,销售单价为x元.(1)、直接写出y与x之间的函数关系式和自变量x的取值范围;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?(3)、该店主热心公益事业,决定从每天的利润中捐出200元给希望工程,为了保证捐款后每天剩余利润不低于2200元,求销售单价x的范围.25. 在正方形中,是边上一点点不与点、重合 , 连接 .【感知】如图 , 过点作交于点易证≌不需要证明 .
【探究】如图 , 取的中点 , 过点作交于点 , 交于点 .
 (1)、求证:;(2)、连接 , 若 , 求的长.
(1)、求证:;(2)、连接 , 若 , 求的长.【应用】如图 , 取的中点 , 连接 , 过点作交于点 , 连接、若 , 求四边形的面积.
26. 如图,在平面直角坐标系中,抛物线与轴交于点 , 与轴交于 , 两点点在点的左侧 , 且点坐标为 , 直线的解析式为 . (1)、求抛物线的解析式;(2)、过点作 , 交抛物线于点 , 点为直线上方抛物线上一动点,连接 , , , 求四边形面积的最大值及相应点的坐标;(3)、将抛物线向左平移个单位,已知点为抛物线的对称轴上一动点,点为平移后的抛物线上一动点.在(2)中,当四边形的面积最大时,是否存在以 , , , 为顶点的四边形为平行四边形?若存在,直接写出点的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、过点作 , 交抛物线于点 , 点为直线上方抛物线上一动点,连接 , , , 求四边形面积的最大值及相应点的坐标;(3)、将抛物线向左平移个单位,已知点为抛物线的对称轴上一动点,点为平移后的抛物线上一动点.在(2)中,当四边形的面积最大时,是否存在以 , , , 为顶点的四边形为平行四边形?若存在,直接写出点的坐标;若不存在,请说明理由.