广西南宁十四中2022-2023学年九年级上学期开学数学试卷
试卷更新日期:2022-09-20 类型:开学考试
一、选择题(本大题共12小题,共36分。)
-
1. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、2. 以下列各组数为边长能构成直角三角形的是( )A、4,5,6 B、3,4,5 C、2,3,4 D、6,8,113. 甲,乙,丙,丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是 , , , , 在本次射击测试中,这四个人成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 如图,在四边形中,对角线和相交于点 , 下列条件不能判断四边形是平行四边形的是( )
 A、 , B、 , C、 , D、 ,5. 如图,矩形的对角线、相交于点 , 点是的中点,若 , 则的长为( )
A、 , B、 , C、 , D、 ,5. 如图,矩形的对角线、相交于点 , 点是的中点,若 , 则的长为( )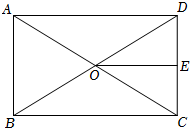 A、3 B、4 C、5 D、66. 如图,直线经过点 , 则关于的方程的解是( )
A、3 B、4 C、5 D、66. 如图,直线经过点 , 则关于的方程的解是( ) A、 B、 C、 D、无法确定7. 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为64元,求平均每次降价的百分率.设平均每次降价的百分率为x,可列方程得( )A、 B、 C、 D、8. 如图,在菱形中,与相交于点 , 的垂直平分线交于点 , 连接 , 若 , 则的度数为( )
A、 B、 C、 D、无法确定7. 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为64元,求平均每次降价的百分率.设平均每次降价的百分率为x,可列方程得( )A、 B、 C、 D、8. 如图,在菱形中,与相交于点 , 的垂直平分线交于点 , 连接 , 若 , 则的度数为( ) A、 B、 C、 D、9. 关于的一元二次方程有两个实根,则实数的取值范围是( )A、 B、 C、且 D、且10. 我国古代数学著作九章算术中记载了一个问题:“今有池方一丈,葭生其中,出水一尺引葭赴岸,适与岸齐问水深几何”丈、尺是长度单位,1丈=10尺其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面水的深度是多少?则水深为( )
A、 B、 C、 D、9. 关于的一元二次方程有两个实根,则实数的取值范围是( )A、 B、 C、且 D、且10. 我国古代数学著作九章算术中记载了一个问题:“今有池方一丈,葭生其中,出水一尺引葭赴岸,适与岸齐问水深几何”丈、尺是长度单位,1丈=10尺其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面水的深度是多少?则水深为( ) A、10尺 B、11尺 C、12尺 D、13尺11. 图(1),在 中, ,点P从点A出发,沿三角形的边以 /秒的速度逆时针运动一周,图(2)是点P运动时,线段 的长度y( )随运动时间x(秒)变化的关系图象,则图(2)中P点的坐标是( )
A、10尺 B、11尺 C、12尺 D、13尺11. 图(1),在 中, ,点P从点A出发,沿三角形的边以 /秒的速度逆时针运动一周,图(2)是点P运动时,线段 的长度y( )随运动时间x(秒)变化的关系图象,则图(2)中P点的坐标是( )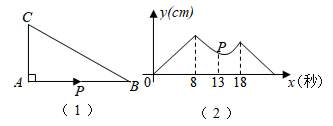 A、 B、 C、 D、12. 如图,抛物线的对称轴是直线 , 并与轴交于 , 两点,若 , 则下列结论中:;;;若为任意实数,则 , 正确的个数是( )
A、 B、 C、 D、12. 如图,抛物线的对称轴是直线 , 并与轴交于 , 两点,若 , 则下列结论中:;;;若为任意实数,则 , 正确的个数是( )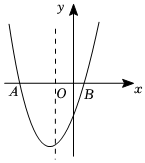 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(本大题共6小题,共18分)
-
13. 若二次根式有意义,则x的取值范围为 .14. 某招聘考试分笔试和面试两种.其中笔试按80%、面试按20%计算加权平均数作为总成绩.小明笔试成绩为90分面试成绩为85分,那么小明的总成绩为分.15. 若一元二次方程的两个实数根为 , , 则的值为 .16. 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=度.
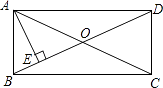 17. 人们把这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比. , , 记 , , , , 则 .18. 如图抛物线与轴交于 , 两点,与轴交于点 , 点是抛物线对称轴上任意一点,若点 , , 分别是 , , 的中点,连接 , , 则的最小值为 .
17. 人们把这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比. , , 记 , , , , 则 .18. 如图抛物线与轴交于 , 两点,与轴交于点 , 点是抛物线对称轴上任意一点,若点 , , 分别是 , , 的中点,连接 , , 则的最小值为 .
三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算:.20. 解方程21. 如图,在平行四边形中, , , 垂足分别为 , , 且 .
 (1)、求证:平行四边形是菱形;(2)、若 , , 求四边形的面积.22. 某水果店在端午节前以10元的价格购进某种苹果2000箱,每箱苹果质量为 , 在出售前需进行挑拣,去掉损坏的部分.现随机抽取了20箱,去掉损坏苹果后称得每箱质量如下:(单位:kg)
(1)、求证:平行四边形是菱形;(2)、若 , , 求四边形的面积.22. 某水果店在端午节前以10元的价格购进某种苹果2000箱,每箱苹果质量为 , 在出售前需进行挑拣,去掉损坏的部分.现随机抽取了20箱,去掉损坏苹果后称得每箱质量如下:(单位:kg)4.7 4.8 4.6 4.5 4.8 4.9 4.8 4.7 4.8 4.7
4.8 4.9 4.7 4.8 4.5 4.7 4.7 4.9 5.0 4.7
整理数据:
质量
4.5
4.6
4.7
4.8
4.9
5.0
数箱箱
2
1
7
a
3
1
分析数据:
平均数
众数
中位数
4.75
b
c
(1)、上述表格中 , , ;(2)、平均数,众数,中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选择其中一个统计量,估算这2000箱苹果共损坏了多少千克?(3)、根据(2)中的结果,求该水果店销售这批苹果时每千克定价为多少元时才不亏本?(结果精确到0.1)23. A、B两地相距 , 甲、乙两人分别开车从地出发前往地,其中甲先出发如图是甲,乙行驶路程 , 随行驶时间变化的图象,请结合图象信息,解答下列问题: (1)、填空:甲的速度为;(2)、分别求出 , 与之间的函数解析式;(3)、求出点的坐标,并写出点的实际意义.24. 某超市采购了两批同样的冰墩墩挂件,第一批花了3300元,第二批花了4000元,第一批每个挂件的进价是第二批的1.1倍,且第二批比第一批多购进25个.(1)、求第二批每个挂件的进价;(2)、两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少?
(1)、填空:甲的速度为;(2)、分别求出 , 与之间的函数解析式;(3)、求出点的坐标,并写出点的实际意义.24. 某超市采购了两批同样的冰墩墩挂件,第一批花了3300元,第二批花了4000元,第一批每个挂件的进价是第二批的1.1倍,且第二批比第一批多购进25个.(1)、求第二批每个挂件的进价;(2)、两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少?

