山东省青岛市2022-2023学年高三上学期数学期初调研检测试卷

试卷更新日期：2022-09-20 类型：开学考试

进入出卷网下载

一、单选题

1. 若 $z (- 3 + i) = 10$ ，则 $z =$ （）

A、 $3 + i$ B、 $- 3 - i$ C、 $- 3 + i$ D、 $3 - i$

查看试题解析
2. 若集合 $A = {x ∣ \sqrt{x} < 1} ， B = {x ∣ 2^{x} \leq \sqrt{2}}$ ，则 $A ∩ B =$ （）

A、 $(- \infty ， \frac{1}{2}]$ B、 $(0 ， \frac{1}{2}]$ C、 $[0 ， \frac{1}{2}]$ D、 $[\frac{1}{2} ， 1)$

查看试题解析
3. 已知 $s i n (α + \frac{π}{4}) = \frac{\sqrt{2}}{4}$ ，则 $s i n 2 α =$ （）

A、 $- \frac{3}{4}$ B、 $\frac{3}{4}$ C、 $\pm \frac{3}{4}$ D、 $- \frac{\sqrt{7}}{4}$

查看试题解析
4. 在 ${(x - \frac{2}{x})}^{6}$ 的展开式中，常数项为（）

A、80 B、-80 C、160 D、-160

查看试题解析
5. 已知 $a = s i n 4 ， b = l n 2 ， c = 2^{0.3}$ ，则（）

A、 $b < a < c$ B、 $c < b < a$ C、 $a < b < c$ D、 $a < c < b$

查看试题解析
6. 已知圆台的上下底面半径分别为1和2，侧面积为 $3 \sqrt{5} π$ ，则该圆台的外接球半径为（）

A、 $\frac{\sqrt{105}}{5}$ B、 $\frac{\sqrt{65}}{4}$ C、 $\frac{\sqrt{185}}{4}$ D、 $\frac{\sqrt{105}}{4}$

查看试题解析
7. 据史书记载，古代的算筹是由一根根同样长短和粗细的小棍制成，如图所示，据《孙子算经》记载，算筹记数法则是：凡算之法，先识其位，一纵十横，百立千僵，千十相望，万百相当.即在算筹计数法中，表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用横式，以此类推.例如表示62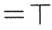，表示26，现有5根算筹，据此表示方式表示两位数（算筹不剩余且个位不为0），则这个两位数大于30的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{5}$

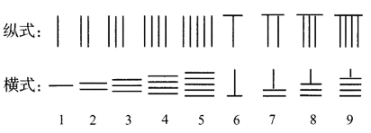查看试题解析
8. 抛物线有一条重要性质：从焦点发出的光线，经过抛物线上的一点反射后，反射光线平行于拋物线的轴.如图所示，从拋物线 $C ： y^{2} = 2 p x (p > 0)$ 的焦点 $F$ 向 $x$ 轴上方发出的两条光线 $a ， b$ 分别经抛物线上的 $A ， B$ 两点反射，已知两条入射光线与 $x$ 轴所成角均为 $\frac{π}{3}$ ，且 $| F B | + | F A | = 8$ ，则两条反射光线 $a^{'} ， b^{'}$ 之间的距离为（）

A、 $\sqrt{3}$ B、4 C、2 D、 $2 \sqrt{3}$

查看试题解析

二、多选题

9. 已知直线 $l_{1} ： 4 x - 3 y + 4 = 0 ， l_{2} ： (m + 2) x - (m + 1) y + 2 m + 5 = 0 (m \in R)$ ，则（）

A、直线 $l_{2}$ 过定点 $(- 3 ， - 1)$ B、当 $m = 1$ 时， $l_{1} ⊥ l_{2}$ C、当 $m = 2$ 时， $l_{1} ∥ l_{2}$ D、当 $l_{1} ∥ l_{2}$ 时，两直线 $l_{1} ， l_{2}$ 之间的距离为1

查看试题解析
10. 已知函数 $f (x) = s i n (4 x + \frac{π}{6})$ ，则（）

A、 $f (x)$ 的最小正周期为 $\frac{π}{2}$ B、 $f (x)$ 在 $[- \frac{π}{8} ， \frac{π}{8}]$ 上单调递增 C、 $f (x)$ 的图象关于点 $(\frac{5 π}{24} ， 0)$ 中心对称 D、 $f (x)$ 在 $[- \frac{π}{24} ， \frac{23 π}{24}]$ 上有4个零点

查看试题解析
11. 在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为菱形， $∠ A B C = \frac{π}{3} ， P A ⊥$ 平面 $A B C D$ ， $P A = A B = 2 ， E$ 为线段 $P B$ 的中点， $F$ 为线段 $B C$ 上的动点，则（）

A、平面 $A E F ⊥$ 平面 $P B C$ B、三棱锥 $C - P E D$ 的体积为 $\frac{\sqrt{3}}{3}$ C、 $E F$ 与平面 $A B C D$ 所成角的最小值为 $\frac{π}{6}$ D、 $A E$ 与 $P C$ 所成角的余弦值为 $\frac{1}{4}$

查看试题解析
12. 已知函数 $f (x) ， g (x)$ 的定义域为 $R ， g^{'} (x)$ 为 $g (x)$ 的导函数，且 $f (x) + g^{'} (x) - 5 = 0$ ， $f (x) - g^{'} (4 - x) - 5 = 0$ ，若 $g (x)$ 为偶函数，则（）

A、 $f (4) = 5$ B、 $g (2) = 0$ C、 $f (- 1) = f (- 3)$ D、 $f (1) + f (3) = 10$

查看试题解析

三、填空题

13. 已知 $A (2 ， 3) ， B (1 ， - 3) ， C (6 ， - 3) ， D$ 为 $B C$ 中点，则 $\vec{A D} \cdot \vec{B C} =$ .

查看试题解析
14. 某地有6000名学生参加考试，考试后数学成绩 $X$ 近似服从正态分布 $N (110 ， σ^{2})$ ，若 $P (90 \leq X \leq 110) = 0.45$ ，则估计该地学生数学成绩在130分以上的人数为.

查看试题解析
15. 已知函数 $f (x) = x (e^{x} - a)$ 有两个极值点，则实数 $a$ 的取值范围是.

查看试题解析
16. 已知双曲线 $E ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左､右焦点分别为 $F_{1} ， F_{2} ， | F_{1} F_{2} | = 4$ ，若线段 $x - y + 4 = 0 (- 2 \leq x \leq 8)$ 上存在点 $M$ ，使得线段 $M F_{2}$ 与 $E$ 的一条渐近线的交点 $N$ 满足： $| F_{2} N | = \frac{1}{4} | F_{2} M |$ ，则 $E$ 的离心率的取值范围是.

查看试题解析

四、解答题

17. 记 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 $a c o s B + b c o s A = 2 c c o s C$ .

(1)、求 $C$ ；

(2)、若 $△ A B C$ 为锐角三角形，求 $\frac{a}{b}$ 的取值范围.

查看试题解析
18. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B ⊥ B C ， A A_{1} = A B = 2$ .

(1)、证明： $A_{1} C ⊥ A B_{1}$ ；

(2)、若三棱锥 $B_{1} - A_{1} A C$ 的体积为 $\frac{2 \sqrt{2}}{3}$ ，求二面角 $A_{1} - B_{1} C - A$ 的大小.

查看试题解析
19. 记关于 $x$ 的不等式 $x^{2} - 4 n x + 3 n^{2} \leq 0 (n \in N^{*})$ 的整数解的个数为 $a_{n}$ ，数列 ${b_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，满足 $4 T_{n} = 3^{n + 1} - a_{n} - 2$ .

(1)、求数列 ${b_{n}}$ 的通项公式；

(2)、设 $c_{n} = 2 b_{n} - λ {(- \frac{3}{2})}^{n}$ ，若对任意 $n \in N^{*}$ ，都有 $c_{n} < c_{n + 1}$ 成立，试求实数 $λ$ 的取值范围.

查看试题解析
20. 为了有针对性地提高学生体育锻炼的积极性，某中学需要了解性别因素是否对学生体育锻炼的经常性有影响，为此随机抽查了男女生各100名，得到如下数据：
性别
锻炼
不经常
经常
女生
40
60
男生
20
80
附： $χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$
$α$
0.010
0.005
0.001
$x_{α}$
6.635
7.879
10.828

(1)、根据小概率值 $α = 0.005$ 的独立性检验，分析性别因素与学生体育锻炼的经常性有无关联；

(2)、从这200人中随机选择1人，已知选到的学生经常参加体育锻炼，求他是男生的概率；

(3)、为了提高学生体育锻炼的积极性，学校设置了“学习女排精神，塑造健康体魄”的主题活动，在该活动的某次排球训练课上，甲乙丙三人相互做传球训练.已知甲控制球时，传给乙的概率为 $\frac{2}{3}$ ，传给丙的概率为 $\frac{1}{3}$ ；乙控制球时，传给甲和丙的概率均为 $\frac{1}{2}$ ；丙控制球时，传给甲的概率为 $\frac{3}{4}$ ，传给乙的概率为 $\frac{1}{4}$ .若先由甲控制球，经过3次传球后，乙队员控制球的次数为 $X$ ，求 $X$ 的分布列与期望 $E (X)$ .

查看试题解析
21. 在平面直角坐标系 $O x y$ 中，动圆 $P$ 与圆 $C_{1} ： x^{2} + y^{2} + 2 x - \frac{45}{4} = 0$ 内切，且与圆 $C_{2} ： x^{2} + y^{2} - 2 x + \frac{3}{4} = 0$ 外切，记动圆 $P$ 的圆心的轨迹为 $E$ .

(1)、求轨迹 $E$ 的方程；

(2)、不过圆心 $C_{2}$ 且与 $x$ 轴垂直的直线交轨迹 $E$ 于 $A ， M$ 两个不同的点，连接 $A C_{2}$ 交轨迹 $E$ 于点 $B$ .
（i）若直线 $M B$ 交 $x$ 轴于点 $N$ ，证明： $N$ 为一个定点；
（ii）若过圆心 $C_{1}$ 的直线交轨迹 $E$ 于 $D ， G$ 两个不同的点，且 $A B ⊥ D G$ ，求四边形 $A D B G$ 面积的最小值.

查看试题解析
22. 已知函数 $f (x) = {\begin{array}{l} x l n x - x ， & x > 0 ， \\ 0 ， & x = 0 . \end{array}$

(1)、求 $f (x)$ 的最小值；

(2)、函数 $y = f (x)$ 的图象是一条连续不断的曲线，记该曲线与 $x$ 轴围成图形的面积为 $S$ ，证明： $S < e - \frac{1}{2}$ ；

(3)、若 $(x + \frac{m}{n}) e^{\frac{m}{x} + n} \leq x^{n + 1} l n x (m \in R ， n > 0)$ 对于任意 $x \in [1 ， + ∞)$ 恒成立，证明： $m + n \leq 0$ .

查看试题解析

性别	锻炼
性别	不经常	经常
女生	40	60
男生	20	80

$α$	0.010	0.005	0.001
$x_{α}$	6.635	7.879	10.828