浙江省温州市苍南县部分校平行班2022-2023学年九年级上学期返校考数学试卷

试卷更新日期：2022-09-20 类型：开学考试

进入出卷网下载

一、选择题（本大题共10小题，共40分。）

1. 计算 $- 3 + 2$ 的结果是（）

A、1 B、-1 C、5 D、-5

查看试题解析
2. 如图是某校参加各兴趣小组的学生人数分布扇形统计图，由图可知，该校参加人数最多的兴趣小组是（）

A、棋类 B、书画 C、演艺 D、球类

查看试题解析
3. 在绣山中学某次“数学讲坛”比赛中，有9名学生参加决赛，他们的决赛成绩各不相同，其中一名学生想要知道自己是否能进入前5名，他不仅要知道自己的成绩，还要知道这9名学生成绩的（）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析
4. 计算 ${(2 x^{2})}^{3}$ 的结果是（）

A、 $6 x^{5}$ B、 $6 x^{6}$ C、 $8 x^{6}$ D、 $8 x^{5}$

查看试题解析
5. 若反比例函数 $y = \frac{k - 1}{x}$ 的图象位于第二、四象限，则 $k$ 的取值范围是（）

A、 $k < 1$ B、 $k > 1$ C、 $k > 0$ D、 $k < 0$

查看试题解析
6. 不等式组 ${\begin{array}{l} x + 2 > 1 \\ 3 - x \leq 0 \end{array}$ 的解是（）

A、 $x > - 1$ B、 $x \geq 3$ C、 $- 1 < x \leq 3$ D、 $- 1 \leq x < 3$

查看试题解析
7. 每年的6月5日为世界环境保护日，为提高学生环境保护意识，某校对100名学生进行“保护环境知多少”测试，抽取部分统计如下表：

成绩（分）

60

70

80

90

100

人数（人）

7

20

23

42

8

本次测验成绩的众数为（）

A、80分 B、85分 C、90分 D、100分

查看试题解析
8. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x + k = 0$ 有两个不相等的实数根，则k的值可以是（）

A、-2 B、1 C、2 D、3

查看试题解析
9.
如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB长是（　　）

A、2海里 B、2sin55°海里 C、2cos55°海里 D、2tan55°海里

查看试题解析
10. 如图，四边形 $O A B C$ 中， $B C / / A O$ ， $A B ⊥ O A$ 交 $x$ 轴正半轴于点 $A$ ，反比例函数 $y = \frac{k}{x} (k > 0)$ 经过点 $C$ ，交 $A B$ 的中点于 $D$ ， $O D$ 平分 $∠ C O A$ ，若 $B C = 2$ ，则 $k$ 的值为（）

A、12 B、 $8 \sqrt{2}$ C、8 D、 $4 \sqrt{3}$

查看试题解析

二、填空题（本大题共6小题，共30分）

11. 分解因式： $a^{2} - 4 b^{2} =$ ．

查看试题解析
12. 一个不透明的袋子中装有仅颜色不同的1个红球，2个绿球和3个白球，从袋子中随机摸出一个小球，则摸出的小球恰好是一个红球概率为．

查看试题解析
13. 如图， $A C / / B D$ ， $A B ⊥ B C$ ， $∠ 1 = 35 °$ ，则 $∠ 2 =$ $° .$

查看试题解析
14. 方程 $\frac{x}{x - 3} = \frac{2}{3 - x}$ 的根是．

查看试题解析
15. 如图，直线 $y = - 2 x + 3$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ ， $B$ ，将这条直线向左平移与 $x$ 轴、 $y$ 轴分别交于点 $C$ ， $D .$ 若 $A B = B D$ ，则点 $C$ 的坐标是．

查看试题解析
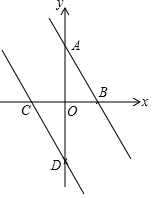16. 某校购买了一套乒乓球桌和自动发球机，侧面如图1所示，球台长度AB=274cm，发球机紧贴球台端线点A处，高出球台的部分AC=12cm，出球管道CD=5 $\sqrt{2}$ cm，若将水平状态的CD绕点C逆时针旋转45°到CD的位置，发球机模式为“一跳球"，路线呈抛物线，离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm，则EB=cm

查看试题解析

三、计算题（本大题共1小题，共10分）

17.

(1)、计算： $\sqrt{4} - (1 - \sqrt{2})^{0} + | - 3 |$ ；

(2)、先化简，再求值： $(m - n)^{2} + (m + n) (m - n) - 2 m^{2}$ ，其中 $m = 3$ ， $n = \frac{1}{2}$ ．

查看试题解析

四、解答题（本大题共7小题，共70分。）

18. 一只不透明的袋子中装有4个球，其中2个白球和2个黑球，它们除颜色外都相同．

(1)、求摸出一个球是白球的概率．

(2)、摸出一个球，记下颜色后不放回，再摸出1个球，求两次摸到的球颜色相同的概率（要求画树状图或列表）．

查看试题解析
19. 如图，已知四边形 $A B C D$ 是平行四边形， $A E ⊥ B D$ 于点 $E$ ， $C F ⊥ B D$ 于点 $F$ ，延长 $A E$ ， $C F$ 分别交 $C D$ ， $A B$ 于点 $M$ ， $N$ ．

(1)、求证：四边形 $C M A N$ 是平行四边形；

(2)、已知 $D E = 4$ ， $F N = 3$ ，求 $B N$ 的长．

查看试题解析
20. 如图，在方格纸中，点 $A$ ， $B$ ， $P$ 都在格点上．请按要求画出以 $A B$ 为边的格点图形．

(1)、在图甲中画出一个三角形，使 $B P$ 平分该三角形的面积．

(2)、在图乙中画出一个至少有一组对边平行的四边形，使 $A P$ 平分该四边形的面积．

查看试题解析
21. 某商家对A、B两款学生手表的销售情况进行了为期五个月的调查统计，期间两款手表的月销售量统计图如图所示。

(1)、请求出A款学生手表这五个月的总销售量以及B款学生手表4月-5月的销售量增长率；

(2)、参考这五个月的销售情况，请对这两款手表未来的进货、销售方面提出你的建议。

查看试题解析
22. 如图，抛物线 $y = - x^{2} + b x + c (b > 0)$ ，交x轴于点A、B，交y轴于点C，已知A的横坐标为－1.

(1)、求点B的坐标.（用含b的代数式表示）

(2)、抛物线的对称轴交x轴于点D，连结BC，平移线段CB，使点C与D重合，此时点B恰好落在抛物线上，求b的值.

查看试题解析

23. 下表是某奶茶店的一款奶茶近两天的销售情况．

销售情况	销售数量（单位：杯）		销售收入（单位：元）
销售情况	小杯	大杯	销售收入（单位：元）
第一天	20	30	460
第二天	25	25	450

(1)、问这款奶茶小杯和大杯的销售单价各是多少元？

(2)、已知这款奶茶小杯成本4元

/

杯，大杯成本5元

/

杯，奶茶店每天只能供应80杯该款奶茶，其中小杯不少于10杯，求该款奶茶一天的最大利润．（销售利润

=

销售收入

-

成本）

(3)、为了满足市场的需求，奶茶店推出每杯2元的加料服务，顾客在选完杯型后可以自主选择加料或者不加料．小明恰好用了208元购买该款奶茶，其中小杯不加料的数量是总杯数的

\frac{1}{3}

，则小明这款奶茶大杯加料的买了杯．

查看试题解析

24. 如图，抛物线 $y = - x^{2} + m x + 5$ 交 $x$ 轴正半轴于点 $A$ ，交 $y$ 轴于点 $B$ ，过抛物线的顶点 $C$ 作 $C D ⊥ x$ 轴，交 $x$ 轴正半轴于点 $D$ ，交 $A B$ 于点 $E$ ， $P$ 为射线 $E D$ 上一点，作点 $P$ 关于直线 $A B$ 的对称点 $Q$ ， $P Q$ 交 $A B$ 于点 $F$ ，连结 $C Q$ ，已知 $O D = 2$ ．

(1)、求证： $△ A O B$ 是等腰直角三角形．

(2)、当点 $P$ 的纵坐标是1时，判断点 $Q$ 是否落在抛物线上，并说明理由．

(3)、连结 $B P$ 若四边形 $C E F Q$ 的面积是 $△ P E F$ 的面积的4倍，求点 $P$ 的坐标．

查看试题解析

成绩（分）	60	70	80	90	100
人数（人）	7	20	23	42	8