四川省巴中市恩阳区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-20 类型:期中考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的为( )A、 B、 C、 D、2. 下列各组线段中,是成比例线段的是( )A、2,3,5,6 B、1,2,3,5 C、1,3,3,7 D、2,3,4,63. 二次根式 中x的取值范围是( )A、x≥6 B、x≤6 C、x<6 D、x>64. 估计×+的运算结果应在( )A、6到7之间 B、7到8之间 C、8到9之间 D、9到10之间5. 关于x的一元二次方程(m﹣1)x2+5x+m2﹣3m+2=0,常数项为0,则m值等于( )A、1 B、2 C、1或2 D、06. 是下列哪个一元二次方程的根( )A、 B、 C、 D、7. 新冠肺炎是一种传染性极强的疾病,如果有一人患病,经过两轮传染后有81人患病,设每轮传染中平均一个人传染了x个人,下列列式正确的是( )A、 B、 C、 D、8. 某口罩厂六月份的口罩产量为100万只,由于市场需求量减少,八月份的产量减少到81万只设该厂七八月份的口罩产量的月平均减少率为x,可列方程为( )A、 B、 C、 D、9. 下列各组图形必相似的是( ).A、任意两个等腰三角形 B、两条边之比为2∶3的两个直角三角形 C、两条边成比例的两个直角三角形 D、斜边和一条直角边对应成比例的两个直角三角形10. 如图,已知,中,P为AB上一点,在下列四个条件中:(1);(2);(3);(4) , 能满足与相似的条件是( ).
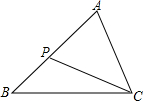 A、(1)(2)(4) B、(1)(3)(4) C、(2)(3)(4) D、(1)(2)(3)11. 如图所示,四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,E、F分别是PA、PQ两边的中点;当点P在BC边上移动的过程中,线段EF的长度将( ).
A、(1)(2)(4) B、(1)(3)(4) C、(2)(3)(4) D、(1)(2)(3)11. 如图所示,四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,E、F分别是PA、PQ两边的中点;当点P在BC边上移动的过程中,线段EF的长度将( ).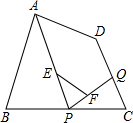 A、先变大,后变小 B、保持不变 C、先变小,后变大 D、无法确定12. 美是一种感觉,当人体下半身长与身高的比值越接近黄金分割比时,越给人一种美感.如图,某女士身高165cm,下半身长x与身高L的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( ).
A、先变大,后变小 B、保持不变 C、先变小,后变大 D、无法确定12. 美是一种感觉,当人体下半身长与身高的比值越接近黄金分割比时,越给人一种美感.如图,某女士身高165cm,下半身长x与身高L的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( ).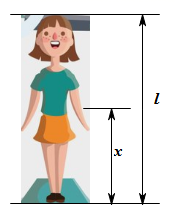 A、4cm B、6cm C、8cm D、10cm
A、4cm B、6cm C、8cm D、10cm二、填空题
-
13. 计算 × 的值是 .14. 若 ,则 .15. 如下图, , 若 , , , 则 , .
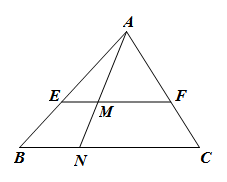 16. 已知方程的两根分别为和 , 则 .17. 已知a、b、c满足 , , , 则 .18. 点G为的重心,如果 , , , 则的面积为 .
16. 已知方程的两根分别为和 , 则 .17. 已知a、b、c满足 , , , 则 .18. 点G为的重心,如果 , , , 则的面积为 .三、解答题
-
19. 解方程:(1)、(2)、(3)、(4)、20. 已知x=2+ , y=2﹣ ,
求代数式的值:
(1)、x2﹣y2(2)、21. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
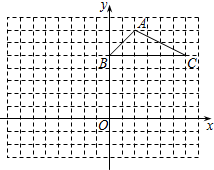 (1)、点A的坐标为 ,点C的坐标为 .(2)、将△ABC向左平移7个单位,请画出平移后的△A1B1C1 . 若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .(3)、以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1:2.请在网格内画出△A2B2C2 , 并写出点A2的坐标: ▲ .22. 已知关于x的一元二次方程有实数根.(1)、求m的取值范围;(2)、若该方程的两个实数根为 , , 且 , 求m的值.23. 如图,△ABC是一张锐角三角形的硬纸片.AD是边BC上的高,BC=40cm,AD=30cm.从这张硬纸片剪下一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.
(1)、点A的坐标为 ,点C的坐标为 .(2)、将△ABC向左平移7个单位,请画出平移后的△A1B1C1 . 若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M1的坐标为 .(3)、以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1:2.请在网格内画出△A2B2C2 , 并写出点A2的坐标: ▲ .22. 已知关于x的一元二次方程有实数根.(1)、求m的取值范围;(2)、若该方程的两个实数根为 , , 且 , 求m的值.23. 如图,△ABC是一张锐角三角形的硬纸片.AD是边BC上的高,BC=40cm,AD=30cm.从这张硬纸片剪下一个长HG是宽HE的2倍的矩形EFGH.使它的一边EF在BC上,顶点G,H分别在AC,AB上.AD与HG的交点为M.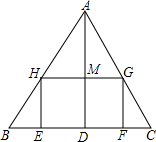 (1)、求证: ;(2)、求这个矩形EFGH的周长.24. 正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)、求证: ;(2)、求这个矩形EFGH的周长.24. 正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.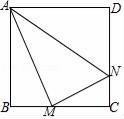 (1)、证明:△ABM∽△MCN;(2)、若△ABM的周长与△MCN周长之比是4:3,求NC的长.25. 阅读下列解题过程:
(1)、证明:△ABM∽△MCN;(2)、若△ABM的周长与△MCN周长之比是4:3,求NC的长.25. 阅读下列解题过程:例:若代数式 , 求a的取值.
解:原式= ,
当a<2时,原式=(2-a)+(4-a)=6-2a=2,解得a=2(舍去);
当2≤a<4时,原式=(a-2)+(4-a)=2=2,等式恒成立;
当a≥4时,原式=(a-2)+(a-4)=2a-6=2,解得a=4;
所以,a的取值范围是2≤a≤4.
上述解题过程主要运用了分类讨论的方法,请你根据上述理解,解答下列问题:
(1)、当3≤a≤7时,化简:=;(2)、请直接写出满足=5的a的取值范围;(3)、若=6,求a的取值.26. 如图,在平面直角坐标系中,已知的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程的两根 , 动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.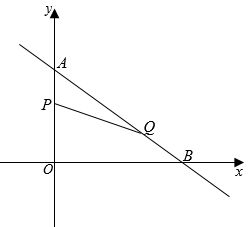 (1)、求A、B两点的坐标;(2)、求当t为何值时,与相似;(3)、当时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,求出M点的坐标;若不存在,请说明理由.
(1)、求A、B两点的坐标;(2)、求当t为何值时,与相似;(3)、当时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,求出M点的坐标;若不存在,请说明理由.