山西省运城市2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-09-19 类型：期中考试

进入出卷网下载

一、单选题

1.
如图，在一密闭的圆柱形玻璃杯中装一半的水，水平放置时，水面的形状是（　　）

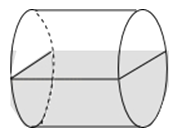A、圆 B、长方形 C、椭圆 D、平行四边形

查看试题解析
2. 山西洪灾发生后，社会许多热心人士主动支援山西，坚持与山西同舟共“晋”．如图是一个正方体的平面展开图，折叠成正方体后与“晋”字相对的字是（）

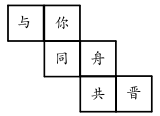A、你 B、同 C、舟 D、共

查看试题解析
3. 一袋大米的质量标识为“ $10 \pm 0.15$ 千克”，则下列大米中质量合格的是（）

A、 $9.80$ 千克 B、 $10.16$ 千克 C、 $9.90$ 千克 D、 $10.21$ 千克

查看试题解析
4. 5G是第五代移动通信技术，5G网络理论下载速度可以达到每秒1300000KB以上.用科学记数法表示1300000是（）

A、13×10⁵ B、1.3×10⁵ C、1.3×10⁶ D、1.3×10⁷

查看试题解析
5. 下列计算正确的是（）

A、 $b - 5 b = - 4$ B、 $2 m + n = 2 m n$ C、 $2 a^{4} + 4 a^{2} = 6 a^{6}$ D、 $- 2 a^{2} b + 5 a^{2} b = 3 a^{2} b$

查看试题解析
6. 下列说法中，正确的是（）

A、 $\frac{m^{2} n}{3}$ 不是整式 B、 $- \frac{3 a b c}{2}$ 的系数是 $- 3$ ，次数是 $3$ C、 $3$ 是单项式 D、多项式 $2 x^{2} y - x y$ 的次数是 $5$

查看试题解析
7. 实数 $a$ ， $b$ 在数轴上的位置如图所示，则下列各式正确的是（）

A、 $a - b > 0$ B、 $a + b > 0$ C、 $a b < 0$ D、 $a b > 0$

查看试题解析
8. 若代数式 $x^{2} + a x - (b x^{2} - x - 3)$ 的值与字母 $x$ 无关，则 $a - b$ 的值为（）

A、 $0$ B、 $- 2$ C、 $2$ D、 $1$

查看试题解析
9. 已知 $3 x^{2} + y = 2$ ， $x^{2} - x y = 3$ ，则 $4 x^{2} - (x y - y) - 1 =$ （）

A、 $2$ B、 $1$ C、 $3$ D、 $4$

查看试题解析
10. 已知 $a$ 和 $b$ 互为相反数（均不为 $0$ ）， $c$ 和 $d$ 互为倒数，表示 $x$ 的数的点到原点的距离为 $3$ ，则 $5 (a + b)^{2} + 12 c d - 2 x =$ （）

A、 $18$ B、 $- 6$ C、 $6$ 或 $- 12$ D、 $6$ 或 $18$

查看试题解析

二、填空题

11. 若单项式 $4 x^{3} y^{m}$ 与 $- \frac{2}{3} x^{n} y^{4}$ 是同类项，则 $m^{n} =$ ．

查看试题解析
12. 一个棱柱有12个顶点，所有的侧棱长的和是48cm，则每条侧棱长是 cm.

查看试题解析
13. 一个两位数，个位数字与十位数字的和为6，设十位数字为x，则这个两位数可表示为．

查看试题解析
14. 对有理数 $a$ ， $b$ 定义运算 $a \otimes b = \frac{a b}{a - b}$ ，则 $3 \otimes (- 6) =$ ．

查看试题解析
15. 下列图案均是用长度相同的小木棒按一定的规律拼搭而成：拼搭第1个图案需4根小木棒，拼搭第2个图案需10根小木棒，…依此规律，拼成第n个图案需要小木棒.

查看试题解析

三、解答题

16.

(1)、 $12 - (- 18) + (- 7) - 20$ ；

(2)、 $(- 81) \div \frac{9}{4} \times \frac{4}{9} \div (- 16)$ ；

(3)、 $(\frac{1}{4} + \frac{1}{6} + \frac{3}{8}) \times (- 24) - 3^{2} \times {(- \frac{1}{3})}^{2}$ ；

(4)、 $- 1^{2020} + (- 2)^{3} \times (- \frac{1}{2}) - | - 1 - 5 |$

查看试题解析
17.

(1)、先化简，再求值：已知 $a = 1$ ， $b = - 2$ ，求代数式 $(6 a^{2} - 2 a b) - 2 (3 a^{2} + 4 a b - \frac{1}{8} b^{2})$ 的值；

(2)、七年级某同学做一道题：“已知两个多项式 $A$ ， $B$ ， $A = x^{2} + 2 x - 1$ ，计算 $A + 2 B$ ”，他误将 $A + 2 B$ 写成了 $2 A + B$ ，结果得到答案 $x^{2} + 5 x - 6$ ，请你帮助他求出正确的答案．

查看试题解析
18.

(1)、一个几何体由一些大小相同的小正方体搭成，如图是从上面看这个几何体的形状图，小正方形中的数字表示在该位置的小正方体的个数，请在网格中画出从正面和左面看到的几何体的形状图．

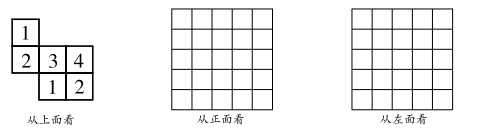(2)、用小立方块搭一几何体，使它从正面看，从左面看，从上面看得到的图形如图所示．请在从上面看到的图形的小正方形中填入相应的数字，使得小正方形中的数字表示在该位置的小立方块的个数．其中，图1填入的数字表示最多组成该几何体的小立方块的个数，图2填入的数字表示最少组成该几何体的小立方块的个数．

查看试题解析
19. “米奇”的形象风靡全球．如图是一张边长为 $x$ ， $y$ 的长方形纸片（脸）和两张半径为 $R$ 的圆纸片（耳朵）组成，在长方形内剪去三个大小一样的半径为 $R$ 的半圆，得到一个“米奇”图案．

(1)、用含 $x$ ， $y$ ， $R$ 的式子表示“米奇”图案的面积 $S$ ；

(2)、当 $x = 4$ ， $y = 5$ ， $R = 2$ 时，求 $S$ 的值．（结果保留 $π$ ）

查看试题解析
20. 一场突如其来的暴雨来袭，我省的取暖物资紧缺，红十字会立即分配了运输取暖物资的任务：一辆配送车，从配送站出发，向东走了 $3$ 千米到达村庄 $A$ ，继续向东走了 $1.5$ 千米到达村庄 $B$ ，然后向西走了 $8.5$ 千米到村庄 $C$ ，最后返回配送站．

(1)、以配送站为原点，向东为正方向，向西为负方向， $1$ 个单位长度表示 $1$ 千米，请你在数轴上标出村庄 $A$ ，村庄 $B$ ，村庄 $C$ 的位置．

(2)、村庄 $A$ 与村庄 $C$ 相距多远？

(3)、若配送车每千米耗油 $0.15$ 升，那么这辆车完成此次运输任务共耗油多少升？

查看试题解析

21. 2020年的“新冠肺炎”疫情的蔓延，使得医用口罩销量大幅增加，某口罩加工厂为满足市场需求计划每天生产5000个，由于各种原因实际每天生产量相比有出入，表格是二月份某一周的生产情况（超产为正，减产为负，单位：个）．

星期	一	二	三	四	五	六	日
增减	+100	-200	+400	-100	-100	+350	+150

(1)、根据记录可知前三天共生产多少个口罩；

(2)、产量最多的一天比产量最少的一天多生产多少个；

(3)、该口罩加工厂实行计件工资制，每生产一个口罩0.2元，本周口罩加工厂应支付工人的工资总额是多少元？

查看试题解析

22. 观察图，解答下列问题．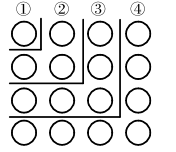

(1)、图中的圆圈被折线隔开分成六层，第一层有 $1$ 个圆圈，第二层有 $3$ 个圆圈，第三层有 $5$ 个圆圈，…，第六层有 $11$ 个圆圈．如果要你继续画下去，第 $n$ 层有个圆圈．

(2)、某一层上有 $65$ 个圆圈，这是第层．

(3)、数图中的圆圈个数可以有多种不同的方法．比如：前两层的圆圈个数和为 $(1 + 3)$ 或 $2^{2}$ ，由此得， $1 + 3 = 2^{2}$ ，同样：由前三层的圆圈个数和得： $1 + 3 + 5 = 3^{2}$ ，由前四层的圆圈个数和得： $1 + 3 + 5 + 7 = 4^{2}$ ， …根据上述规律，从 $1$ 开始的 $n$ 个连续奇数之和是多少？用 $n$ 的代数式把它表示出来

(4)、运用（3）中的规律计算： $73 + 75 + 77 + \cdot \cdot \cdot + 153$ ．

查看试题解析
23. 已知b是最小的正整数，且a，b，c满足 $(c - 6)^{2} + | a + b | = 0$ ，请回答下列问题：

(1)、请直接写出 $a$ ， $b$ ， $c$ 的值， $a =$ ， $b =$ ， $c =$ ．

(2)、如图 $a$ ， $b$ ， $c$ 在数轴上所对应的点分别为 $A$ ， $B$ ， $C$ ，点 $P$ 为一动点，其对应的数为 $x$ ，当点 $P$ 在 $A$ ， $B$ 之间运动时，请化简式子： $| x + 1 | - | x - 1 | - | x + 5 |$ ；（请写出化简过程）

(3)、在（1）和（2）的条件下，若点 $A$ 以每秒 $1$ 个单位长度的速度向左运动，同时，点 $C$ 以每秒 $1$ 个单位长度向右运动，假设经过 $t$ 秒，点 $B$ 与点 $C$ 之间的距离为 $B C$ ，点 $A$ 与点 $B$ 之间的距离为 $A B$ ，则 $B C =$ ， $A B =$ ，并求出 $B C - A B$ 的值．

查看试题解析