内蒙古自治区赤峰市松山区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-09-19 类型:期中考试
一、单选题
-
1. 计算等于( )A、 B、2 C、4 D、2. 2019年10月1日庆祝祖国七十华诞的隆重阅兵活动,由徒步方队、装备方队和空中梯队三部分组成,总规模约1.5万人,各型飞机160余架,装备580台套,是几次阅兵中规模最大的一次. 1.5万这个数用科学记数法表示为 ( )A、150×102 B、15×103 C、1.5×104 D、0.15×1053. 用四舍五入法把3.8963精确到百分位得到的近似数是( )A、3.896 B、3.900 C、3.9 D、3.904. 下列说法中错误的有( )个
⑴0是单项式,⑵是二次单项式,⑶的系数是;⑷与互为倒数;⑸的相反数是
A、4个 B、3个 C、2个 D、1个5. 下列计算正确的是( )A、 B、 C、 D、6. 下列比较大小,正确的是( )A、 B、 C、 D、7. 点 在数轴上的位置如图所示, 为原点, , .若点 所表示的数为 ,则点 所表示的数为( )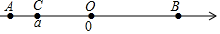 A、 B、 C、 D、8. 、、是有理数且 , 则的值是( )A、 B、3或 C、1 D、或19. 下列说法中错误的是( )
A、 B、 C、 D、8. 、、是有理数且 , 则的值是( )A、 B、3或 C、1 D、或19. 下列说法中错误的是( )①负数的相反数大于它本身;②数轴上原点两侧的数互为相反数;③绝对值等于它本身的有理数是0 ;④两个数相互比较,绝对值大的反而小.
A、①② B、②③ C、①②③ D、②③④10. 若 , 则( )A、 B、5 C、 D、111. 下面四个整式中,不能表示图中阴影部分面积的是( ) A、 B、 C、 D、12. 已知与的和是单项式,则( )A、 , B、 , C、 , D、 ,13. 当多项式不含二次项和一次项时,的值为( )A、 B、 C、 D、14. 如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;如果剪了次,共剪出( )个小正方形?
A、 B、 C、 D、12. 已知与的和是单项式,则( )A、 , B、 , C、 , D、 ,13. 当多项式不含二次项和一次项时,的值为( )A、 B、 C、 D、14. 如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;如果剪了次,共剪出( )个小正方形? A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 如果把向东走3米记作米,那么向西走2米记作米.16. 若长方形的周长为6a,其中一边长为a+b,则另一边的长为 .17. 某同学家长利用他的压岁钱买了理财产品,上周每天的收益情况如下表,周末收盘时,他累计盈利元.
星期
一
二
三
四
五
收益情况(单位:元)
5.8
18. 如图是某月的月历,如果设带阴影的方框正中心的数为 , 则方框中的九个数的和用含的代数式表示是 .
三、解答题
-
19. 计算:(1)、(2)、 .20. 已知数a , b表示的点在数轴上的位置如图所示.
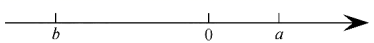 (1)、在数轴上表示出a , b的相反数的位置,并将这四个数从小到大排列;(2)、若数b与其相反数相距16个单位长度,则b表示的数是多少?(3)、在(2)的条件下,若数a与数b的相反数表示的点相距4个单位长度,则a表示的数是多少?21. 先化简,再求值
(1)、在数轴上表示出a , b的相反数的位置,并将这四个数从小到大排列;(2)、若数b与其相反数相距16个单位长度,则b表示的数是多少?(3)、在(2)的条件下,若数a与数b的相反数表示的点相距4个单位长度,则a表示的数是多少?21. 先化简,再求值, 其中| , , .
22. 一辆出租车一天上午以某商场为出发地在东西大街上运行,规定向东为正,向西为负,出租车的行驶里程(单位:)如下:, , , , , , , , , , .
(1)、将最后一名乘客送到目的地时,相对于商场,出租车的位置在哪里?;(2)、这天上午出租车总共行驶了多少?(3)、已知出租车每行驶耗油 , 每升汽油的售价为元.如果不计其他成本,出租车平均每千米收费元,那么这半天出租车盈利(或亏损)了多少元?23. 数学课上,小明同学提出一个观点“一个两位数与它的10倍的和一定能被11整除”.你同意他的观点吗?请结合你学过的知识说明理由.24. 如图①所示是一个长为 , 宽为的长方形,沿图中虚线用剪刀均分成四个相同的小长方形,然后按图②的方式拼图. (1)、你认为图②中的阴影部分的正方形的边长等于 .(2)、请用两种不同的方法列代数式表示图②中阴影部分的面积.
(1)、你认为图②中的阴影部分的正方形的边长等于 .(2)、请用两种不同的方法列代数式表示图②中阴影部分的面积.方法① .
方法② .
(3)、观察图②,你能写出 , , 这三个代数式之间的等量关系吗?(4)、根据(3)题中的等量关系,解决如下问题:若 . , 求的值25. 某学校准备印刷一批证书,现有两个印刷厂可供选择:甲厂收费方式:收制版费1000元,每本印刷费0.5元;
乙厂收费方式:不超过2000本时,每本收印刷费1.5元;超过2000本超过部分每本收印刷费0.25元,若该校印制证书x本.
(1)、若x 不超过2000时,甲厂的收费为元,乙厂的收费为元;(2)、若x 超过2000时,甲厂的收费为元,乙厂的收费为元(3)、当印制证书8000本时应该选择哪个印刷厂更节省费用?节省了多少?(4)、请问印刷多少本证书时,甲乙两厂收费相同?26. 已知:与互为相反数,是最小的正整数,且满足 . (1)、直接写出、、的值: , , .(2)、、、所对应的点分别为、、 , 点为一动点,其对应的数为 , 点在0到2之间运动时(即时),请化简式子:(请写出化简过程).(3)、在(1)(2)的条件下,点、、开始在数轴上运动,若点以每秒1个单位长度的速度向左运动,同时,点和点分别以每秒2个单位长度和5个单位长度的速度向右运动,假设秒钟过后,若点与点之间的距离表示为 . 点与点之间的距离表示为 . 请问:的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求其值.
(1)、直接写出、、的值: , , .(2)、、、所对应的点分别为、、 , 点为一动点,其对应的数为 , 点在0到2之间运动时(即时),请化简式子:(请写出化简过程).(3)、在(1)(2)的条件下,点、、开始在数轴上运动,若点以每秒1个单位长度的速度向左运动,同时,点和点分别以每秒2个单位长度和5个单位长度的速度向右运动,假设秒钟过后,若点与点之间的距离表示为 . 点与点之间的距离表示为 . 请问:的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求其值.