江西省景德镇市乐平市2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-09-19 类型:期中考试
一、单选题
-
1. 我国第七次人口普查于2021年5月11日公布普查结果,显示我国人口数量约为141200万人,将这个数用科学记数法表示为( )A、1.412×108人 B、1.412×109人 C、1.412×1010人 D、1.412×1011人2. 下列每组两个数是互为相反数的是( )A、3和 B、﹣3和﹣ C、﹣3和 D、3和﹣33. 下列几何体中,属于柱体的个数有( )
 A、1个 B、2个 C、3个 D、4个4. 一个正方体六个面分别写上“仁”、“义”、“礼”、“智”、“信”、“孝”这6个字,它的表面展开图如图所示,则“孝”字的相对的面上的字是( )
A、1个 B、2个 C、3个 D、4个4. 一个正方体六个面分别写上“仁”、“义”、“礼”、“智”、“信”、“孝”这6个字,它的表面展开图如图所示,则“孝”字的相对的面上的字是( )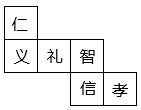 A、礼 B、智 C、义 D、仁5. 如表格是一张日历表,省去了号码数,设①位置的数为x,则②位置的数可表示为( )
A、礼 B、智 C、义 D、仁5. 如表格是一张日历表,省去了号码数,设①位置的数为x,则②位置的数可表示为( )日
一
二
三
四
五
六
①
②
A、2x+7 B、3x﹣7 C、x+12 D、x+106. 如图,在正方体中,沿对角线BD和顶点A所在的平面截出几何体A﹣BCD,则这个几何体的展开图可能是( ) A、
A、 B、
B、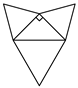 C、
C、 D、
D、 7. 下列与﹣2ab2是同类项的是( )A、﹣2a2b B、 C、3ab2c D、ba28. 如图所示的图形都是由同样大小的长方形按一定的规律组成的.其中第(1)个图形的面积为2,则第15个图形的面积为( )
7. 下列与﹣2ab2是同类项的是( )A、﹣2a2b B、 C、3ab2c D、ba28. 如图所示的图形都是由同样大小的长方形按一定的规律组成的.其中第(1)个图形的面积为2,则第15个图形的面积为( ) A、400 B、425 C、440 D、450
A、400 B、425 C、440 D、450二、填空题
-
9. 如果把收入80元记作+80元,那么支出30元记作10. ﹣ 的倒数是 .11. 多项式a﹣3a2b+2b﹣1的次数是 次.12. 某病人每天下午需要测量血压,该病人上周日收缩压为120单位,下表是该病人这周每天与前一天相比较收缩压的变化情况,则本周星期五的收缩压是 .
星期
一
二
三
四
五
增减
+20
﹣30
﹣25
+15
+30
13. 按如图计算程序进行计算,若输入x=﹣2,则输出y的值为 . 14. 一个正四棱柱,底面是边长为5cm的正方形,高是8cm.则此正四棱柱的表面积为cm215. 某电影院第1排有23个座位,以后每排比前一排多2个座位,则第15排的座位数为个.16. 如图1的三条线段的长如图所示,用n个图1拼成图2的总长度 . (用含n的代数式表示)
14. 一个正四棱柱,底面是边长为5cm的正方形,高是8cm.则此正四棱柱的表面积为cm215. 某电影院第1排有23个座位,以后每排比前一排多2个座位,则第15排的座位数为个.16. 如图1的三条线段的长如图所示,用n个图1拼成图2的总长度 . (用含n的代数式表示)
三、解答题
-
17. 计算:(1)、(+20)﹣(+18)+(﹣30)﹣(﹣23);(2)、;(3)、5﹣1;(4)、()×(﹣36).18. 计算:
①n﹣(﹣n+3);
②4a3﹣3a2b+5ab2+a2b﹣5ab2﹣3a3;
③5(3x﹣2y)﹣7(3x﹣2y)﹣3(3x﹣2y)+(3x﹣2y);
④5x2﹣7x﹣[3x2﹣2(﹣x2+4x﹣1)].
19. 如图是由7个相同的小立方块搭成的几何体.请画出主视图、左视图和俯视图. 20. 已知有理数:﹣1;0;;﹣2.5;4
20. 已知有理数:﹣1;0;;﹣2.5;4 (1)、将这些有理数表示到数轴上;(2)、将这些有理数用“<”号连接起来.21. 如图是一个食品包装盒的表面展开图.
(1)、将这些有理数表示到数轴上;(2)、将这些有理数用“<”号连接起来.21. 如图是一个食品包装盒的表面展开图.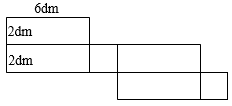 (1)、写出这个包装盒形状的几何名称;(2)、求这个包装盒的表面积.22. 一辆“滴滴车”在一条南北走向的公路上往返行驶,接送客人.向北行驶的路程记为正数,向南行驶的路程记为负数.一天早上,“滴滴车”从汽车站出发,上午每次行驶的路程记录如下(单位:km):5,﹣8,6,﹣7,﹣4,5(1)、这天“滴滴车”在这条公路上行驶过程中,距离汽车站最远多少千米?在汽车站的南方还是北方?(2)、该“滴滴车”每行驶1千米,耗油0.12升,这天接送客人,“滴滴车”共耗油多少升?23. 已知代数式:2(2x+y﹣3)﹣[2x2﹣2(3xy2+x2﹣y)+4x]﹣(3xy2﹣5).(1)、化简代数式.(2)、小贤同学取x,y互为倒数的一对数值代入化简式中,计算得代数式的值为8,那么小贤同学所取的字母x和y的值分别是多少?24. 如图是用棋子摆成的“上”字图案,按照这种规律继续摆下去,通过观察、对比、总结,找出规律,解答下列问题.
(1)、写出这个包装盒形状的几何名称;(2)、求这个包装盒的表面积.22. 一辆“滴滴车”在一条南北走向的公路上往返行驶,接送客人.向北行驶的路程记为正数,向南行驶的路程记为负数.一天早上,“滴滴车”从汽车站出发,上午每次行驶的路程记录如下(单位:km):5,﹣8,6,﹣7,﹣4,5(1)、这天“滴滴车”在这条公路上行驶过程中,距离汽车站最远多少千米?在汽车站的南方还是北方?(2)、该“滴滴车”每行驶1千米,耗油0.12升,这天接送客人,“滴滴车”共耗油多少升?23. 已知代数式:2(2x+y﹣3)﹣[2x2﹣2(3xy2+x2﹣y)+4x]﹣(3xy2﹣5).(1)、化简代数式.(2)、小贤同学取x,y互为倒数的一对数值代入化简式中,计算得代数式的值为8,那么小贤同学所取的字母x和y的值分别是多少?24. 如图是用棋子摆成的“上”字图案,按照这种规律继续摆下去,通过观察、对比、总结,找出规律,解答下列问题. (1)、摆成图1需要枚棋子,摆成图2需要 枚棋子,摆成图3需要枚棋子;(2)、摆成图n需要枚棋子;(3)、七(1)班有46名同学,把每名同学当成一枚“棋子”,能否让这46枚“棋子”按照以上规律恰好站成一“上”字?若能,请问能站成图几?并计算最下面一“横”的学生数;若不能,请说明理由.25. 现象感知 如图1,在数轴上,线段AB的中点为E,点E表示的数与点A、点B表示的数关系存在:=6;线段CD的中点为F,点F表示的数与点C、点D表示的数的关系也存在:=﹣2
(1)、摆成图1需要枚棋子,摆成图2需要 枚棋子,摆成图3需要枚棋子;(2)、摆成图n需要枚棋子;(3)、七(1)班有46名同学,把每名同学当成一枚“棋子”,能否让这46枚“棋子”按照以上规律恰好站成一“上”字?若能,请问能站成图几?并计算最下面一“横”的学生数;若不能,请说明理由.25. 现象感知 如图1,在数轴上,线段AB的中点为E,点E表示的数与点A、点B表示的数关系存在:=6;线段CD的中点为F,点F表示的数与点C、点D表示的数的关系也存在:=﹣2归纳性质 如图2,在数轴上,线段GH的中点为P.
 (1)、如图2,在数轴上,点G、H、P表示的数分别为a,b,c,请猜想a,b,c的等量关系,请写出一等量关系式.小宇同学为了说明a,b,c的等量关系是正确的,采用了字母表示数的方法,设PG=PH=m,从而表示出G、H两点的数(含c和m).请完成小宇的说理过程.
(1)、如图2,在数轴上,点G、H、P表示的数分别为a,b,c,请猜想a,b,c的等量关系,请写出一等量关系式.小宇同学为了说明a,b,c的等量关系是正确的,采用了字母表示数的方法,设PG=PH=m,从而表示出G、H两点的数(含c和m).请完成小宇的说理过程.拓展应用
(2)、如图,点A,B,C在数轴上对应的数分别为﹣3,1,9,它们分别以每秒2个单位长度、1个单位长度和4个单位长度的速度在数轴上同时向左做匀速运动,设同时运动的时间为t秒.若A,B,C三点中,有一点恰为另外两点所连线段的中点,求t的值.