江西省赣州市上犹县2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-09-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各组数中，互为相反数的是（）

A、3和 $\frac{1}{3}$ B、3和－3 C、3和－ $\frac{1}{3}$ D、－3和－ $\frac{1}{3}$

查看试题解析
2. 如果将汽车向北行驶30千米记作＋30千米，那么汽车向南行驶50千米可记作（）

A、＋50千米 B、－50千米 C、＋80千米 D、－20千米

查看试题解析
3. 第七次全国人口普查结果显示，我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为（）

A、 $218 \times 10^{6}$ B、 $21.8 \times 10^{7}$ C、 $2.18 \times 10^{8}$ D、 $0.218 \times 10^{9}$

查看试题解析
4. 人教版初中数学课本宽度约为18.2cm，该近似数18.2精确到（）

A、千分位 B、百分位 C、十分位 D、个位

查看试题解析
5. 下列判断正确的是（）

A、单项式﹣2²x³yz 的次数是5 B、 $\frac{2 m^{2} n}{5}$ 的系数是2 C、3a²bc 与bca²不是同类项 D、3x²﹣y+5xy²是二次三项式

查看试题解析
6.
古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”．从图7中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（）

A、13 =3+10 B、25 =9+16 C、36 =15+21 D、49 = 18+31

查看试题解析

二、填空题

7. 比较大小： $- \frac{5}{4}$ $- \frac{3}{4}$ （用“>”、“<”、“=”号填空）．

查看试题解析
8. $- \sqrt{2}$ 的绝对值是.

查看试题解析
9. 写出一个关于 $x$ 的二次三项式，使它的二次项系数为 $- 1$ ，则这个二次三项式为．

查看试题解析
10. 已知单项式 $3 a^{m} b^{2}$ 与 $- \frac{2}{3} a^{4} b^{n - 1}$ 是同类项，那么 $4 m - n =$ ．

查看试题解析
11. 已知 $a$ 、 $b$ 、 $c$ 是有理数，且 $a + b + c = 0$ ， $a b c < 0$ 则 $\frac{b + c}{| a |} + \frac{a + c}{| b |} + \frac{a + b}{| c |}$ 的值是.

查看试题解析
12. 若a²＝4，|b|＝3，且ab＜0，则a+b＝．

查看试题解析

三、解答题

13. 在数轴上(每一格代表单位长度1)表示出数-2.5， 1，0， |－3|， $\frac{3}{2}$ ，并把它们用“<”连接起来。

查看试题解析
14. 计算：

(1)、（﹣12）﹣（+20）+（﹣8）﹣15；

(2)、 $(\frac{2}{9} - \frac{1}{4} + \frac{1}{18}) \div (- \frac{1}{36})$ ．

查看试题解析
15. ﹣1²⁰²⁰+（﹣3）²×（﹣ $\frac{2}{3}$ ）﹣4²÷|﹣4|．

查看试题解析
16. 先化简，再求值：2（y+3x²+1）﹣3（2x²﹣2xy﹣2），其中x＝6，y＝﹣1．

查看试题解析
17. 有理数a，b，c在数轴上的位置如图：

(1)、用“＞”或“＜”填空：b﹣c0，a+b0，﹣a+c0；

(2)、化简：|b﹣c|+|a+b|﹣|﹣a+c|．

查看试题解析
18. 十一黄金周期间，龙之梦景区7天中每天旅游人数的变化情况如下表（正数表示比9月30日多的人数，负数表示比9月30日少的人数）：
日期
1日
2日
3日
4日
5日
6日
7日
人数变化/万人
$+ 0.5$
$+ 0.7$
$+ 0.8$
$- 0.4$
$- 0.6$
$+ 0.2$
$- 0.1$

(1)、请判断7天内游客人数量最多和最少的各是哪一天？它们相差多少万人？

(2)、如果9月30日旅游人数为2万人，平均每人消费300元，请问该景区在此7天内总收入为多少万元？

查看试题解析
19. 元旦周期间，某风景区门票价格为：成人票每张80元，学生票是成人票的一半．励志学校初中部七年级有a名学生和b名老师；八年级学生人数是七年级人数的三倍，八年级老师是七年级老师人数的三倍．

(1)、两个年级去该风景区的人数分别为：七年级人，八年级人．（用含a，b的代数式表示）

(2)、若他们一起去该风景区，则门票费用共需多少元（用含a，b的代数式表示）？若a＝230，b＝34，求两个年级门票费用的总和．

查看试题解析
20. 如图，用五个正方形ADCB、DGHE、EHPF、MPON、NOWS和一个缺角的长方形QBCFMS，其中FM=a，CF=3，SW=b．

(1)、求AD的长（用含a和b的式子表示）．

(2)、求长方形AGWQ的周长（用含a和b的式子表示）．

查看试题解析
21. 某同学做一道数学题，已知两个多项式A、B，B＝3x²y﹣5xy+x+7，试求A+B，这位同学把A+B看成A﹣B，结果求出的答案为6x²y+12xy﹣2x﹣9．

(1)、求多项式A；

(2)、请你替这位同学求出的正确答案；

(3)、求A﹣3B的值，如果当x取任意数值时A﹣3B的值是一个定值，则y的值是多少？

查看试题解析
22. 已知：b是最小的正整数，且a、b满足 ${(c - 5)}^{2}$ ＋ $| a + b |$ ＝0，请回答问题：

(1)、请直接写出a、b、c的值；

(2)、数轴上a、b、c所对应的点分别为A、B、C，点M是A、B之间的一个动点，其对应的数为m，请化简 $| 2 m |$ （请写出化简过程）；

(3)、在（1）（2）的条件下，点A、B、C开始在数轴上运动．若点A以每秒1个单位长度的速度向左运动．同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动．假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB．请问：BC－AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．

查看试题解析
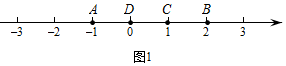
23. 定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就称点C是 $[A ， B]$ 的美好点．
例如；如图1，点A表示的数为 $- 1$ ，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是 $[A ， B]$ 的美好点；又如，表示0的点D到点A的距离是1，到点B的距高是2，那么点D就不是 $[A ， B]$ 的美好点，但点D是 $[B ， A]$ 的美好点．
如图2，M，N为数轴上两点，点M所表示的数为 $- 7$ ，点N所表示的数为2．

(1)、点E，F，G表示的数分别是 $- 3$ ， 6.5，11，其中是 $[M ， N]$ 美好点的是；写出 $[N ， M]$ 美好点H所表示的数是．

(2)、现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动．当t为何值时，点P恰好为M和N的美好点？

查看试题解析

日期	1日	2日	3日	4日	5日	6日	7日
人数变化/万人	$+ 0.5$	$+ 0.7$	$+ 0.8$	$- 0.4$	$- 0.6$	$+ 0.2$	$- 0.1$