河北省邢台市威县2021-2022学年七年级上学期期中数学试题

试卷更新日期：2022-09-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个算式中运算结果为2022的是（）

A、 $2021 + (- 1)$ B、 $2021 - (- 1)$ C、 $- 2021 \times (- 1)$ D、 $2022 \div (- 1)$

查看试题解析
2. $(- \frac{5}{6}) \times (- \frac{5}{6}) \times (- \frac{5}{6}) \times (- \frac{5}{6}) \times (- \frac{5}{6})$ 可表示为（）

A、 $- \frac{5^{5}}{6}$ B、 $5 \times (- \frac{5}{6})$ C、 ${(- \frac{5}{6})}^{5}$ D、 $- \frac{5}{6^{5}}$

查看试题解析
3. 下列选项中，两个整式的结果相同的是（）

A、 $3 (x - 1)$ 和 $3 x - 1$ B、 $x^{2} + x^{2}$ 和 $2 x^{4}$ C、 $x + 2 y$ 和 $3 x y$ D、 $- 0.8 a b$ 和 $\frac{1}{5} a b - b a$

查看试题解析
4. 有理数a在数轴上的对应点的位置如图所示，如果有理数b满足 $a < b < - a$ ，那么b的值不可能是（）

A、2 B、3 C、 $- 1$ D、 $- 2$

查看试题解析

5. 如图所示的是嘉淇同学的答题情况，则她的得分应是（）

姓名嘉淇得分？

填空题（每小题20分，共100分

① $- 1$ 的绝对值是1．

②2的倒数是 $- 2$ ．

③ $- 2$ 的相反数是 $\frac{1}{2}$ ．

④ $0^{2021} =$ 2021

⑤若 $- 5 x^{2} y^{m}$ 与 $2 x^{n} y^{3}$ 是同类项，则 $m + n$ 的值为5．

A、100分 B、80分 C、60分 D、40分

查看试题解析

6. 已知一天有86400秒，一年按365天计算共有31536000秒，“中国飞人”苏炳添经过5年（约157680000秒），从里约到东京，以9秒83创亚洲纪录的成绩，成为首位闯进奥运会男子百米决赛的中国人．将157680000科学记数法表示为 $a \times 10^{n}$ ，则n的值为（）

A、9 B、8 C、7 D、4

查看试题解析
7. 将 $- 2$ 、1、2、3、4这五个数填入下列方框中，使行、列三个数的和相等，则其中正确的是（）

A、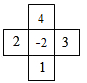 B、 C、 D、

查看试题解析
8. 下列说法错误的是（）

A、单项式 $\frac{x^{3} y}{5}$ 的次数是4，系数是 $\frac{1}{5}$ B、单项式 $- 2 m n x$ 的次数是3，系数是 $- 2$ C、多项式 $3 x^{2} - x + 1$ 是二次三项式 D、多项式 $- x^{2} + 5 x$ 的一次项是 $5 x$ ，常数项是1

查看试题解析
9. 已知甲数比乙数的6倍少5，则下列说法正确的是（）

A、设乙数为x，则甲数为 $6 (x - 5)$ B、设甲数为x，则乙数为 $\frac{1}{6} x + 5$ C、设甲数为x，则乙数为 $\frac{1}{6} (x + 5)$ D、设甲数为x，则乙数为 $\frac{1}{6} (x - 5)$

查看试题解析
10. 如图， $A + B$ 一定是（）
A：我是一个五次多项式
B：我也是一个五次多项式

A、不高于五次多项式或单项式 B、四次多项式 C、五次多项式 D、十次多项式

查看试题解析
11. 体育课上全班女生进行百米测验，达标成绩为18秒，下面是第一小组8名女生的成绩记录，其中“+”表示成绩大于18秒，“-”表示成绩小于18秒，则这个小组女生的达标率是（）

$- 2$

$+ 0.3$

0

$+ 0.2$

$+ 1.2$

$- 1$

$+ 0.5$

$- 0.4$

A、62.5% B、37.5% C、50% D、75%

查看试题解析
12. 某公司2020年1～3月平均每月亏损150万元，4～7月平均每月盈利200万元，8～10月平均每月盈利170万元，11～12月共亏损420万元，则该公司2020年总的盈亏情况是（）

A、盈利440万元 B、盈利940万元 C、亏损440万元 D、亏损290万元

查看试题解析
13. 在某学校庆祝“中国共产党建党100周年”的活动上，小青同学用围棋棋子按照某种规律摆成如图所示的“100”字样．按照这种规律，第n个“100”字样图案的棋子个数是（）

A、 $5 n + 6$ B、 $5 n + 7$ C、 $4 n + 8$ D、 $4 n + 9$

查看试题解析
14. 已知当 $x = 1$ 时，多项式 $a x^{3} + b x + 2022$ 的值为2023；则当 $x = - 1$ 时，多项式 $a x^{3} + b x + 2022$ 的值为（）

A、2024 B、2022 C、2021 D、2019

查看试题解析
15. 疫情期间，口罩的原材料提价，因而厂家决定对口罩进行提价，现有三种方案：（1）第一次提价5%，第二次提价10%；（2）第一次提价10%，第二次提价5%；（3）第一、二次提价均为7.5%，三种方案哪种提价最多，下列说法正确的是（）

A、方案（1） B、方案（2） C、方案（3） D、三种方案相同

查看试题解析
16. 正整数按如图所示的规律排列，则第 $n (n \geq 5)$ 行第5列的数为（）

A、 $n^{2} - 3$ B、 $n^{2} - 4$ C、 $n^{2} - 5$ D、 $n^{2} - 6$

查看试题解析

二、填空题

17. 计算：

(1)、 $- {(- 1)}^{5} =$ ；

(2)、 $- 6 + 2 \times (- 1) =$ ．

查看试题解析
18. 如图，这是2021年6月份的日历表，我们任意圈出一竖列上相邻的三个数．

(1)、若最上方的数为9，则圈出的三个数的和是．

(2)、设中间的一个数为a，则圈出的三个数的和是．

查看试题解析
19. 已知 $A = 3 x^{2} - x + 2 y - 4 x y ， B = 2 x^{2} - 3 x - y + x y$ ．

(1)、化简 $6 A - 9 B =$ ．

(2)、若 $x + y = \frac{3}{7} ， x y = 2$ ，则 $6 A - 9 B$ 的值为．

查看试题解析

三、解答题

20. 根据图示的对话解答下列问题．
已知a与2互为相反数． b与 $- \frac{1}{3}$ 互为倒数．

(1)、a= ， b= ．

(2)、已知 $| m - a | + | b + n | = 0$ ，求 $m n$ 的绝对值．

查看试题解析
21. 阅读下列解题过程．
计算： $(- 25) \div (\frac{1}{3} - 1 \frac{1}{2} - 3) \times 6$ ．

解：原式 $= (- 25) \div (- \frac{25}{6}) \times 6$ （第一步）

$= (- 25) \div (- 25)$ （第二步）

$= - 1$ （第三步）

解答问题：

(1)、上面解答过程有两处错误，第一处是第步，错误的原因是；第二处是第步，错误的原因是．

(2)、请你写出正确的解题过程．

查看试题解析
22. 如图，在数轴上有A，B两点若点C表示的数与点B表示的数相距4个单位长度，且在原点O的右边．

(1)、请直接在数轴上标出点C．

(2)、将点A向右移动2个单位长度，点B向左移动2个单位长度，求移动后A，B，C三个点所表示的数中最小的数与最大的数相距的单位长度．

查看试题解析

23. 某仓库在一周的货品运输中，进出情况如下表所示（进库为正，出库为负，单位：吨）：

星期一	星期二	星期三	星期四	星期五	星期六	星期日	合计
$+ 26$	$- 16$	$+ 42$	$- 30$	■	$- 25$	$- 9$	$+ 8$

表中星期五的进出数被墨水涂污了

(1)、请你算出星期五仓库的进出数．

(2)、如果仓库进出的装卸费都是每吨50元，那么这一周要付多少元装卸费？

查看试题解析

24. 观察表格中两个多项式及其相应的值，回答问题：

x	…	$- 2$	$- 1$	0	1	2	…
$- 2 x + 4$	…	8	6	4	2	a	…
$3 x - 5$	…	$- 11$	$- 8$	$- 5$	$- 2$	b	…

(1)、（初步感知）

根据表中信息可知： $a =$ ； $b =$ ．

(2)、（归纳规律）

表中 $- 2 x + 4$ 的值的变化规律：x的值每增加1， $- 2 x + 4$ 的值就减少2．类似地， $3 x - 5$ 的值的变化规律：．

(3)、（问题解决）

请直接写出一个含x的多项式，要求x的值每增加1，多项式的值就减小5，且当 $x = 0$ 时，多项式的值为6．

查看试题解析

25. 观察下面三行：
$- 3$ ， 9， $- 27$ ， 81，…①
1， $- 3$ ， 9， $- 27$ ， …②
$- 2$ ， 10， $- 26$ ， 82…③

(1)、第①行的数按什么规律排列？

(2)、第②③行数与第①行数分别有什么关系？

(3)、取每行数的第7个数，计算这三个数的和．

查看试题解析
26. 秋风起，桂花飘香，也就进入了吃螃蟹的最好季节清代文人李渔把秋天称作“蟹秋”，意为错过了螃蟹，便是错过了整个秋季，小贤去水产市场采购大闸蟹，极品母蟹每只150元，至尊公蟹每只75元．商家在开展促销活动期间，向客户提供以下两种优惠方案．方案①：极品母蟹和至尊公蟹都按定价的80%付款；方案②：买一只极品母蟹送一只至尊公蟹．现小贤要购买极品母蟹30只，至尊公蟹 $x (x > 30)$ 只．

(1)、按方案①购买极品母蟹和至尊公蟹共需付款（用含x的式子表示）元；按方案②购买极品母蟹和至尊公蟹共需付款（用含x的式子表示）元．

(2)、当 $x = 40$ 时，通过计算说明此时按哪种方案购买较合算．

(3)、若两种优惠方案可同时使用，当 $x = 40$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方案，并说明理由．

查看试题解析