安徽省皖南八校2022-2023学年高三上学期数学开学考试试卷

试卷更新日期：2022-09-19 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $M = {y ∣ y = 2^{x}} ， N = {y ∣ y = \sqrt{1 - x^{2}}}$ ，则 $M ∩ N =$ （）

A、 ${x ∣ 0 < x < 1}$ B、 ${x ∣ 0 < x ⩽ 1}$ C、 ${x ∣ x ⩽ 1}$ D、 ${x ∣ x > 0}$

查看试题解析
2. 若 $z (1 + 2 i) = 2 - i$ （ $i$ 为虚数单位），则复数 $z =$ （）

A、 $- i$ B、 $i$ C、1 D、-1

查看试题解析
3. 已知向量 $\vec{a} = (- 2 ， m) ， \vec{b} = (1 ， - 2)$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $m$ 的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
4. 设 $a = {0.7}^{- 0.5}$ ， $b = {log}_{0.5}^{0.7}$ ， $c = {log}_{0.7}^{5}$ ，则（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > a > b$ D、 $c > b > a$

查看试题解析
5. 某滑冰馆统计了2021年11月1日到30日某小区居民在该滑冰馆的锻炼天数，得到如图所示的频率分布直方图（将频率视为概率），则下列说法正确的是（）

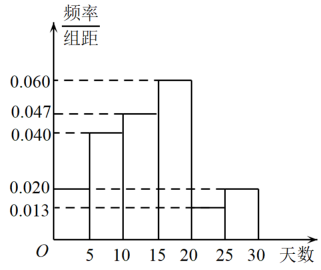A、该小区居民在该滑冰馆的锻炼天数在区间 $(25 ， 30]$ 内的最少 B、估计该小区居民在该滑冰馆的锻炼天数的中位数为16 C、估计该小区居民在该滑冰馆的锻炼天数的平均值大于14 D、估计该小区居民在该滑冰馆的锻炼天数超过15天的概率为0.456

查看试题解析
6. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $a_{3} + a_{5} = - 10 ， S_{6} = - 42$ ，则 $S_{10} =$ （）

A、6 B、10 C、12 D、20

查看试题解析
7. “ $m = - 1$ ”是“直线 $l_{1} ： m x + 2 y + 1 = 0$ 与直线 $l_{2} ： \frac{1}{2} x + m y + \frac{1}{2} = 0$ 平行”的（）

A、充要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要

查看试题解析
8. 若曲线 $y = l n x + x^{2}$ 的一条切线的斜率为3，则该切线的方程可能为（）

A、 $3 x - y - 1 = 0$ B、 $3 x - y + 1 = 0$ C、 $3 x - y - 2 = 0$ D、 $3 x - y - 1 - l n 2 = 0$

查看试题解析
9. 函数 $f (x) = t a n (2 x - \frac{π}{3})$ 的图象的一个对称中心为（）

A、 $(\frac{π}{12} ， 0)$ B、 $(\frac{7 π}{12} ， 0)$ C、 $(- \frac{5 π}{12} ， 0)$ D、 $(- \frac{π}{12} ， 0)$

查看试题解析
10. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2 ， P$ 为 $C C_{1}$ 的中点，点 $Q$ 在四边形 $D C C_{1} D_{1}$ 内（包括边界）运动，若 $A Q$ $∥$ 平面 $A_{1} B P$ ，则 $A Q$ 的最小值为（）

A、1 B、 $\frac{3 \sqrt{2}}{2}$ C、 $\sqrt{5}$ D、 $\sqrt{7}$

查看试题解析
11. 已知点 $M$ 在抛物线 $C ： y^{2} = 2 p x (p > 0)$ 上，若以点 $M$ 为圆心半径为5的圆与抛物线 $C$ 的准线相切，且与 $x$ 轴相交的弦长为6，则 $p =$ （）

A、2 B、8 C、2或8 D、6

查看试题解析
12. 已知函数 $y = f (x + 1)$ 的图象关于直线 $x = - 3$ 对称，且对 $\forall x \in R$ 都有 $f (x) + f (- x) = 2$ 当 $x \in (0 ， 2]$ 时， $f (x) = x + 2$ .则 $f (2022) =$ （）

A、-1 B、1 C、2 D、-2

查看试题解析

二、填空题

13. （x﹣ $\frac{1}{x}$ ）⁴的展开式中的常数项为．

查看试题解析
14. 已知 $0 < α < \frac{π}{2} ， s i n α = \frac{3}{5} ， t a n (α - β) = - \frac{1}{3}$ ，则 $t a n β =$ .

查看试题解析
15. 已知正四棱锥 $P - A B C D$ 的底面边长为3，高为2，若该四棱锥的五个顶点都在一个球面上，则球心到四棱锥侧面的距离为.

查看试题解析
16. 已知双曲线 $C ： \frac{x^{2}}{6} - \frac{y^{2}}{3} = 1$ 的右焦点为 $F_{2}$ ，过点 $F_{2}$ 斜率为 $k$ 的直线 $l$ 与双曲线 $C$ 的右支交于 $A ， B$ 两点，点 $P (- 2 \sqrt{3} ， 0)$ ，若 $△ A B P$ 的外心 $Q$ 的横坐标为0，则直线 $l$ 的方程为.

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 满足 $a_{1} = 1 ， a_{n + 1} = 3 a_{n} (n \in N^{*})$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、证明： $\frac{1}{a_{1}} + \frac{1}{a_{2}} + ⋯ + \frac{1}{a_{n}} < \frac{3}{2}$ .

查看试题解析
18. 已知 $△ A B C$ 的内角 $A ， B ， C$ 所对的边分别是 $a ， b ， c$ ，满足 $\frac{a}{b} = \frac{c o s A + 1}{\sqrt{3} s i n B}$ .

(1)、求角 $A$ ；

(2)、若 $b + c = 2 a$ ，且 $△ A B C$ 外接圆的直径为 $2$ ，求 $△ A B C$ 的面积.

查看试题解析
19. 产品的质量是一个企业在市场中获得消费者信赖的重要因素，某企业对出厂的每批次产品都进行性能测试.某检验员在某批次的产品中抽取5个产品进行性能测试，现有甲､乙两种不同的测试方案，每个产品随机选择其中的一种进行测试，已知选择甲方案测试合格的概率为 $\frac{1}{2}$ ，选择乙方案测试合格的概率为 $\frac{3}{4}$ ，且每次测试的结果互不影响.

(1)、若3个产品选择甲方案，2个产品选择乙方案.
（i）求5个产品全部测试合格的概率；
（ii）求4个产品测试合格的概率.

(2)、若测试合格的产品个数的期望不小于3，求选择甲方案进行测试的产品个数.

查看试题解析
20. 如图，在三棱锥 $P - A B C$ 中， $A B ⊥ B C ， A B = B C = 2 ， P A = P B = P C = 2 \sqrt{2} ， O$ 为 $A C$ 的中点.

(1)、证明： $A C ⊥$ 平面 $P B O$ ；

(2)、若 $M$ 为棱 $B C$ 的中点，求二面角 $M - P A - C$ 的正弦值.

查看试题解析
21. 已知椭圆 $M ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左､右焦点为 $F_{1}$ ， $F_{2}$ ，且左焦点坐标为 $(- \sqrt{2} ， 0)$ ， $P$ 为椭圆上的一个动点， $∠ F_{1} P F_{2}$ 的最大值为 $\frac{π}{2}$ .

(1)、求椭圆 $M$ 的标准方程；

(2)、若过点 $(- 2 ， - 4)$ 的直线 $l$ 与椭圆 $M$ 交于 $A ， B$ 两点，点 $N (2 ， 0)$ ，记直线 $N A$ 的斜率为 $k_{1}$ ，直线 $N B$ 的斜率为 $k_{2}$ ，证明： $\frac{1}{k_{1}} + \frac{1}{k_{2}} = 1$ .

查看试题解析
22. 已知函数 $f (x) = - a x^{2} + x l n x - x$ .

(1)、若 $f (x)$ 有两个极值点，求实数 $a$ 的取值范围；

(2)、当 $a = 0$ 时，求函数 $h (x) = f (x) - x + \frac{2}{x}$ 的零点个数.

查看试题解析