安徽省皖江名校联盟2022-2023学年高三上学期数学8月联考试卷

试卷更新日期：2022-09-19 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $M = {0 ， 1 ， 2} ， N = {x ∣ 0 < x < 2}$ ，则 $M ∪ N =$ （）

A、 ${0 ， 1 ， 2}$ B、{1} C、 $(0 ， 2)$ D、 $[0 ， 2]$

查看试题解析
2. 已知复数 $z = 1 - i + \frac{a}{1 - i}$ 为纯虚数，则实数 $a =$ （）

A、-1 B、1 C、-2 D、2

查看试题解析
3. 某农科院学生为研究某花卉种子的发芽率 $y$ 和温度 $x$ （单位： $^{°} C$ ）的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据 $(x_{i} ， y_{i}) (i = 1 ， 2 ， ⋯ ， 20)$ 得到下面的散点图.由此散点图，在 $1 0^{°} C$ 至 $4 0^{°} C$ 之间，下面四个回归方程类型中最适宜作为发芽率 $y$ 和温度 $x$ 的回归方程类型的是（）

A、 $y = a x + b$ B、 $y = a x^{2} + b$ C、 $y = a l n x + b$ D、 $y = a \cdot e^{x} + b$

查看试题解析
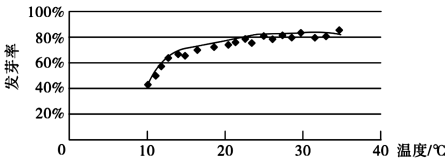4. 设抛物线 $y = \frac{1}{12} x^{2}$ 上一点 $P$ 到 $x$ 轴的距离是1，则点 $P$ 到该抛物线焦点的距离是（）

A、3 B、4 C、7 D、13

查看试题解析
5. 某小区因疫情需求，物业把招募的5名志原者中分配到3处核酸采样点，每处采样点至少分配一名，则不同的分配方法共有（）

A、150 种 B、180 种 C、200 种 D、280 种

查看试题解析
6. 设直线 $m x + n y + 1 = 0 (m > 0 ， n > 0)$ 经过点 $(- 2 ， - 1)$ ，则 $\frac{1}{m} + \frac{2}{n}$ 的最小值为（）

A、16 B、8 C、4 D、2

查看试题解析
7. 如图，某港口一天从6时到18时的水深曲线近似满足函数 $y = A s i n (ω x + φ) + 5 (A > 0 ， ω > 0 ， - \frac{π}{2} < φ < \frac{π}{2})$ .据此可知当天12时的水深为（）

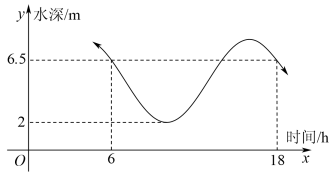A、3.5 B、4 C、 $5 - \frac{3 \sqrt{2}}{2}$ D、 $5 - \frac{3 \sqrt{3}}{2}$

查看试题解析
8. 已知直线 $l$ ： $3 x + 4 y + m = 0$ （ $m > 0$ ）被圆 $C$ ： $x^{2} + y^{2} + 2 x - 2 y - 6 = 0$ 所截的弦长是圆心 $C$ 到直线 $l$ 的距离的2倍，则 $m =$ （）

A、6 B、8 C、9 D、11

查看试题解析
9. 在棱长均等的正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，直线 $A B_{1}$ 与 $B C_{1}$ 所成角的余弦值为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
10. 已知奇函数 $f (x)$ 满足 $f (- x) = f (x + 2)$ ，当 $x \in [0 ， 1]$ 时， $f (x) = 2 x^{2}$ ，则 $f (7) =$ （）

A、-2 B、-1 C、1 D、2

查看试题解析
11. 已知球 $O$ 的半径为3，其内接圆柱的体积最大值为（）

A、 $4 \sqrt{3} π$ B、 $6 \sqrt{3} π$ C、 $12 \sqrt{3} π$ D、 $18 \sqrt{3} π$

查看试题解析
12. 设 $a = 1.1 e^{0.9} ， b = 0.99 e ， c = 0.9 e^{1.1}$ ，则（）

A、 $c > a > b$ B、 $c > b > a$ C、 $a > b > c$ D、 $a > c > b$

查看试题解析

二、填空题

13. 已知等边三角形 $A B C$ 的边长为 $1 ， \vec{B D} = - 2 \vec{D C}$ ，则 $\vec{A C} \cdot \vec{A D} =$ .

查看试题解析
14. 从2，3，4，5，6这5个数字中任取3个，则所取3个数之和为偶数的概率为

查看试题解析
15. 已知点 $P$ 为曲线 $y = l n x$ 上的动点，则 $P$ 到直线 $y = x + 4$ 的最小距离为.

查看试题解析
16. 若双曲线的焦点关于渐近线的对称点恰好在该双曲线上，则该双曲线的离心率为.

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 是公差不为0的等差数列， $a_{1} = 2$ ，且 $a_{3}$ 为 $a_{1}$ 与 $a_{11}$ 的等比中项.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = 2^{n} a_{n}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
18. 记 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，且 $2 b = 3 c ， B = 2 C$ .

(1)、求 $c o s C$ ；

(2)、若 $a = 5$ ，求 $c$ .

查看试题解析
19. 为了监控某一条生产线的生产过程，从其产品中随机抽取100件，测量这些产品的质量指标值，由测量结果得到如图所示的频率分布直方图，其中质量指标值落在区间 $[55 ， 65) ， [65 ， 75) ， [75 ， 85]$ 内的频率是公比为 $\frac{1}{2}$ 的等比数列.

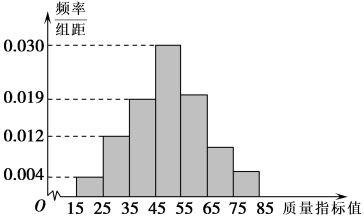(1)、求这些产品质量指标值落在区间 $[75 ， 85]$ 内的频率；

(2)、若将频率视为概率，从该条生产线的这种产品中随机抽取3件，记这3件产品中质量指标位于区间 $[45 ， 75)$ 内的产品件数为 $X$ ，求 $X$ 的分布列与数学期望.

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形， $P A ⊥$ 平面 $A B C D ， P A = A B$ ， $P D = 3 F D ， B E = 3 E P$ .

(1)、求证： $A E ⊥ F C$ ；

(2)、求 $A E$ 与平面 $A C F$ 所成角的余弦值.

查看试题解析
21. 已知线段 $M N$ 的长度为3，其端点 $M ， N$ 分别在 $x$ 轴与 $y$ 轴上滑动，动点 $P$ 满足 $\vec{N P} = 2 \vec{P M}$ .

(1)、求动点 $P$ 的轨迹 $C$ 的方程；

(2)、当点 $M$ 坐标为 $(\frac{3 \sqrt{2}}{2} ， 0)$ ，且点 $P$ 在第一象限时，设动直线 $l$ 与 $C$ 相交于 $A ， B$ 两点，且两直线 $P A 、 P B$ 的斜率互为相反数，求直线 $l$ 的斜率.

查看试题解析
22. 已知函数 $f (x) = \frac{e^{x}}{x + 2}$ .

(1)、求 $f (x)$ 的单调性；

(2)、证明： $f (x) \geq \frac{\sqrt{x + 1}}{2}$ .

查看试题解析