人教版八上数学第十一章11.3.2多边形内角和 课时易错题三刷（第三刷）
试卷更新日期：2022-09-19 类型：同步测试
一、单选题
-
1. 一个多边形的每一个外角都为 ，这个多边形是（ ）A、四边形 B、六边形 C、八边形 D、十边形2. 一个多边形截去一个角后，形成新多边形的内角和为2 520°，则原多边形的边数为（ ）A、15 B、16 C、13或15 D、15或16或173. 小明一笔画成了如图所示的图形，则 的度数为（ ）
A、360° B、540° C、600° D、720°4. 下列说法中，正确的个数有（ ）①若三条线段中有两条线段之和大于第三条线段，则以这三条线段为边可作一个三角形；
②一个三角形中，至少有一个角不小于60°；
③三角形的外角大于与它不相邻的任意一个内角；
④一个多边形的边数每增加一条，这个多边形的内角和就增加180°；
A、1个 B、2个 C、3个 D、45. 小明在计算某多边形的内角和时，由于马虎漏掉了一个角，结果得到970°，则原多边形是一个（ ）A、七边形 B、八边形 C、九边形 D、十边形6. 四边形ABCD中，∠A+∠C=∠B+∠D，∠A的外角为120°，则∠C的度数为（ ）A、36° B、60° C、90° D、120°7. 已知一个n边形的每一个外角都相等，一个内角与其相邻的一个外角的度数之比是 ，则n的值是（ ）A、8 B、9 C、10 D、12二、填空题
-
8. 已知三角形的三个外角的度数比为 ，则它的最大内角的度数为.9. 一个多边形的内角和比它的外角和的2倍还多180°，则它是边形．10. 一个多边形的每一个内角都是135°，则它的边数为 ．11. 如图，小亮从点A出发，沿直线前进15米后向左转30°，再沿直线前进15米，又向左转30°…… 照这样走下去，他第一次回到出发地点A时，共走了米．
12. 如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，若∠A=100°，则∠1+∠2+∠3+∠4= ．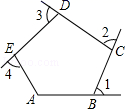
三、解答题
-
13. 一个多边形的内角和是它的外角和的4倍，求这个多边形的边数和对角线条数．14. 若两个多边形的边数之比是1：2，内角和度数之和为1440°，求这两个多边形的边数．15. 小红把一副直角三角板按如图所示的方式摆放在一起，其中 ， ， ， ，求 的度数.
四、综合题
-
16. 一个多边形除一内角外，其余内角和与外角和之和为1560°.(1)、求该多边形的边数；(2)、若该多边形为正多边形，求每一个外角的度数.17. 看对话答题：
小梅说：这个多边形的内角和等于1125°
小红说：不对，你少加了一个角
问题：
(1)、他们在求几边形的内角和?(2)、少加的那个内角是多少度?18.
(1)、如图1，∠ADC=120°，∠BCD=140°，∠DAB和∠CBE的平分线交于点F，则∠AFB的度数是；(2)、如图2，若∠ADC= ， ∠BCD= ， 且 ， ∠DAB和∠CBE的平分线交于点F，则∠AFB=（用含 ， 的代数式表示）；(3)、如图3，∠ADC= ， ∠BCD= ， 当∠DAB和∠CBE的平分线AG，BH平行时， ， 应该满足怎样的数量关系？请说明理由；(4)、如果将（2）中的条件改为 ， 再分别作∠DAB和∠CBE的平分线，∠AFB与 ， 满足怎样的数量关系？请画出图形并直接写出结论.