人教版八上数学第十二章12.2全等三角形的判定 课时易错题三刷（第一刷）

试卷更新日期：2022-09-19 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如图，在 △ABC 中 AB=AC ， ∠B=∠ACD=45° ，D，E是BC上两点，且 ∠DAE=45° ，过点A作 AF⊥AD ，垂足是A，过点C作 CF⊥BC ，垂足是C，CF交AF于点F，连接EF.给出下列结论：① △ABD≌△ACF ；② DE=EF ；③若 S△ADE=10 ， S△CEF=4 ，则 S△ABC=24 ；④ BD+CE=DE .其中正确结论的字号是（   ）

    A、①②③ B、②③④ C、①③④ D、①②④

    查看试题解析

二、填空题

  • 2. 如图，已知CB⊥AD ， AE⊥CD ， 垂足分别为B ， E ， AE、BC相交于点F ， 若AB＝BC＝8，CF＝2，连结DF ， 则图中阴影部分面积为 ．

    查看试题解析

  • 3. 如图，在由6个相同的小正方形拼成的网格中，∠2﹣∠1＝°．

    查看试题解析

三、解答题

  • 4. 已知：Rt △ ABC中，∠B＝90°，D是BC上一点，DF⊥BC交AC于点H，且DF＝BC，FG⊥AC交BC于点E.求证：AB＝DE.

    查看试题解析

  • 5. 如图，等边△ABC的内部有一点D，连接BD，以BD为边作等边△BDE ， 连接AD，CE，求证：AD=CE ．

    查看试题解析

  • 6. 如图，在△ABC中，∠ACB=90° ， CE⊥AB于点E ， AD=AC ， AF平分∠CAB交CE于点F ， DF的延长线交AC于点G ． 求证：DF∥BC ．

    查看试题解析

四、综合题

  • 7. 如图，D是△ABC的边AB上一点，CF//AB，DF交AC于E点，DE＝EF.

    (1)、求证：△ADE≌△CFE.
    (2)、若AB＝5.5，CF＝4，求BD的长.

    查看试题解析

  • 8. 如图1，在△ABC中，BE、CF分别平分∠ABC和∠ACB，BE和CF相交于D点．

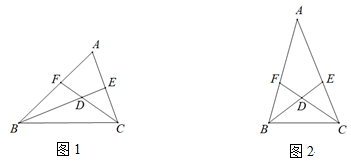    (1)、求证：∠BDC=90°+12∠A；
    (2)、如图2，若∠A＝∠ABE，求证：EB+EC＝BC+BF．

    查看试题解析

  • 9. 已知：在△ABC中，AB＝AC，直线l过点A ．

    (1)、如图1，∠BAC＝90°，分别过点B，C作直线l的垂线段BD，CE，垂足分别为D，E．

    ①依题意补全图1；

    ②用等式表示线段DE，BD，CE之间的数量关系，并证明；

    (2)、如图2，当∠BAC≠90°时，设∠BAC＝α（0°＜ α ＜180°），作∠CEA＝∠BDA＝α，点D，E在直线l上，直接用等式表示线段DE，BD，CE之间的数量关系为 ．

    查看试题解析

  • 10. 如图，在△ABC中，∠ABC＝45°，AH⊥BC于点H，D为AH上一点，且BD=AC，直线BD与AC交于点E，连接EH．

    (1)、求证：DH=CH；
    (2)、判断BE与AC的位置关系，并证明你的结论；
    (3)、求∠BEH的度数．

    查看试题解析

  • 11. 如图，AC与BD交于点O，AD=CB ， E、F是BD上两点，且AE=CF ， DE=BF ． 证明：

    (1)、∠D=∠B；
    (2)、AC与BD互相平分．

    查看试题解析

  • 12. 如图，△ABC中，AB=AC ， 点P在AB上，点Q在线段AC的延长线上，PB=CQ ， PQ与BC相交于点D．点F在BC上，过点P作BC的垂线，垂足为E，∠BPE=∠FPE ．

    (1)、求证：PF=CQ ．
    (2)、请猜测：线段BE、DE、CD数量关系为 ．

    查看试题解析

  • 13. 如图，已知∠A＝∠E，AB＝EB，点D在AC边上，且∠ABE＝∠CBD．

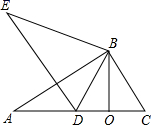    (1)、求证：△EBD≌△ABC．
    (2)、如果O为CD中点，∠BDE＝65°，求∠OBC的度数．

    查看试题解析

  • 14.                
    (1)、（阅读理解）

    课外兴趣小组活动时，老师提出了如下问题：

    如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：

    由已知和作图能得到△ADC≌△EDB的理由是____.

    A、SSS B、SAS C、AAS D、HL
    (2)、求得AD的取值范围是____.
    A、6＜AD＜8 B、6≤AD≤8 C、1＜AD＜7 D、1≤AD≤7
    (3)、（感悟）

    解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.

    （问题解决）

    如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF.求证：AC＝BF.

    查看试题解析

  • 15. 如图1，已知A，E，F，C在同一条直线，AE=CF，过E，F分别作DE⊥AC，BF⊥AC，AB=CD．

    (1)、求证：DB平分EF；
    (2)、若△DEC的边EC沿AC方向移动，其余条件不变，如图2，上述结论是否仍成立？请说明理由．

    查看试题解析

  • 16. 如图（1），已知△ABC和△AED均为等腰三角形，AB=AC，AD=AE，且∠BAC＝∠EAD．

    (1)、求证：CD=BE；
    (2)、将△ABC绕点A旋转到如图（2）的位置，（1）中的结论仍然成立吗？证明你的结论；
    (3)、如图（2），连结EC，若点P是EC的中点，连结PB并延长至点F，使CF＝CD．求证：∠EBP＝∠BFC．

    查看试题解析

  • 17. 如图

    (1)、如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF＝12∠BAD，线段EF、BE、FD之间的关系是；（不需要证明）
    (2)、如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF＝12∠BAD，（1）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证明．
    (3)、如图3，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝12∠BAD，（1）中的结论是否仍然成立？若成立，请证明．若不成立，请写出它们之间的数量关系，并证明．

    查看试题解析

  • 18.             

    (1)、如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°．探究图中线段EF，BE，FD之间的数量关系．

    小明同学探究的方法是：延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，

    他的结论是（直接写结论，不需证明）；

    (2)、如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC，CD上的点，且∠EAF是∠BAD的二分之一，上述结论是否仍然成立，并说明理由．
    (3)、如图3，四边形ABCD是边长为5的正方形，∠EBF=45°，直接写出三角形DEF的周长．

    查看试题解析