2022-2023初数北师大版八年级上册第七章平行线的证明 章末检测
试卷更新日期：2022-09-18 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 下列语句中，不是命题的是（ ）A、两点确定一条直线 B、同位角相等 C、垂线段最短 D、连接、两点2. 能说明命题“对于任意实数 ， ”是假命题的反例为（ ）A、 B、 C、 D、3. 下列四个生活，生产现象：
①从A地到B地架设电线，总是尽可能沿着线段AB架设；②把弯曲的公路改直，就能缩短路程；③用两个钉子就可以把木条固定在墙上；④植树时，只要定出两棵树的位置，就能确定同一行树所在的直线.其中可用公理“两点之间，线段最短”来解释的现象是（ ）
A、①② B、①③ C、②④ D、③④4. 下列叙述错误的是（ ）A、所有的命题都有条件和结论 B、所有的命题都是定理 C、所有的定理都是命题 D、所有的公理都是真命题5. 将一副直角三角尺如图放置，已知∠EAD=∠E=45°，∠C=30°，AE∥BC，求∠AFD的度数，以下是打乱的推理过程：①∵∠E=45°，②∴∠AFD=∠E＋∠EAC=45°＋30°=75°；③∵∠C=30°，AE∥BC，④∴∠EAC=∠C=30°．推理步骤正确的是（ ）
A、①②③④ B、①④③② C、③④①② D、③②①④6. 在证明命题“若 ， 则”是假命题时，下列选项中所举反例错误的是（ ）A、 B、 C、 D、7. 下面的语句是假命题的是（ ）A、同旁内角互补 B、钝角的补角是锐角 C、垂线段最短 D、直角的补角是直角8. 下列命题中是真命题的是（ ）A、实数由有理数和无理数组成 B、实数分为正实数和负实数 C、若 ， 则a=b D、是个分数9. a、b、c是同一平面内的三条直线，下列说法错误的是（ ）A、若a⊥b，b//c，则a⊥c B、若a⊥b，b⊥c，则a⊥c C、若a//b，b⊥c，则a⊥c D、若a//b，b//c，则a//c10. 定理：三角形的一个外角等于与它不相邻的两个内角的和．已知：如图，∠ACD是△ABC的外角．
求证：∠ACD＝∠A＋∠B．
证法1：如图，
∵∠A＋∠B＋∠ACB＝180°（三角形内角和定理）
又∵∠ACD＋∠ACB＝180°（平角定义），
∴∠ACD＋∠ACB＝∠A＋∠B＋∠ACB（等量代换）．
∴∠ACD＝∠A＋∠B（等式性质）
证法2：如图，
∵∠A＝88°，∠B＝58°，
且∠ACD＝146°（量角器测量所得）
又∵146°＝88°＋58°（计算所得）
∴∠ACD＝∠A＋∠B（等量代换）
下列说法正确的是（ ）
A、证法1还需证明其他形状的三角形，该定理的证明才完整 B、证法1用严谨的推理证明了该定理 C、证法2用特殊到一般法证明了该定理 D、证法2只要测量够一百个三角形进行验证，就能证明该定理二、填空题（每题4分，共24分）
-
11. 把命题“同位角相等”改写成“如果……那么……”的形式为 ．12. 三角形的任意两边之和大于第三边是命题．（填写真或假）13. 数学课上，老师要求同学们利用三角板画两条平行线．如图，小华的画法：①将含角三角尺的最长边与直线重合，用虚线作出一条最短边所在直线；②再次将含角三角尺的最短边与虚线重合，画出最长边所在直线 ， 则 ． 你认为他画图的依据是 ．
14. 一次数学测试，满分为100分.测试分数出来后，同桌的李华和吴珊同学把他俩的分数进行计算，李华说：我俩分数的和是160分，吴珊说：我俩分数的差是60分.那么，对于下列两个命题：①俩人的说法都是正确的；②至少有一人说错了；③俩人的说法都是错的.其中真命题是.（用序号填写）15. 若用一组x ， y的值说明命题“若 ， 则”是假命题，则这样的一组值可以是x= ， y= ．16. 下列命题中：①两点的所有连线中，线段最短；②不等式两边加同一个数，不等号的方向改变；③等式两边加同一个数，结果仍相等；④两条直线被第三条直线所截，同位角相等．是假命题的是：（填编号）三、解答题（共8题，共66分）
-
17. 如图，已知点C在线段AB上，AC＝6，点D是线段AB的中点，点E是线段BC的中点．求DE的长．
请把下面的解题过程补充完整：
解：因为点D是线段AB的中点，
所以DB＝ ▲ ；
因为点E是线段BC的中点，
所以BE＝ ▲ ；
因为DE＝DB﹣BE，
所以DE＝ ▲ ﹣ ▲ ＝ ▲ ；
因为AC＝6，
所以DE＝ ▲ ．
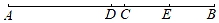18. 在小学，我们曾经通过动手操作，利用拼图的方法研究了三角形三个内角的数量关系．如图，把三角形ABC分成三部分，然后以某一顶点（如点B）为集中点，把三个角拼在一起，观察发现恰好构成了平角，从而得到了“三角形三个内角的和是180°”的结论．但是，通过本学期的学习我们知道：由观察、实验、归纳、类比、猜想得到的结论还需要通过证明来确认它的符合题意性．小聪认真研究了拼图的操作方法，形成了证明命题“三角形三个内角的和是180°”的思路：
①画出命题对应的几何图形；
②写出已知，求证；
③受拼接方法的启发画出辅助线；
④写出证明过程．
请你参考小聪解决问题的思路，写出证明该命题的完整过程．
19.(1)、如图1，在△ABC中，D是AB上一点，E是AC上一点，BE、CD相交于点F ， ∠A＝62°，∠ACD＝35°，∠ABE＝20°．求：∠BFD的度数．对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．
解：∵∠BDC＝∠A+∠ACD（ ▲ ），
∴∠BDC＝62°+35°＝97°（等量代换）．
∵∠BFD+∠BDC+∠ABE＝ ▲ （ ▲ ），
∴∠BFD＝180°﹣∠BDC﹣∠ABE＝180°﹣97°﹣20°＝63°（等式的性质）．
(2)、如图2，把一个长方形的纸ABCD沿对角线折叠（长方形对边平行且相等，四个角是直角），重合部分△FBD是个什么三角形？请证明你的结论．20. 如图1所示， 、 都是直角．
(1)、试猜想 与 在数量上的关系是相等、互余还是互补的关系？你能用推理的方法说明你的猜想是否正确吗？(2)、当 绕着点O旋转到图2的位置时，你原来的猜想还成立吗？21. 如图，已知四个关系式：①AC＝DC；②BC＝EC；③∠DCA＝∠ECB：④AB＝DE．
(1)、从上面四个关系式中任取三个为条件，余下的一个为结论，组成一个命题．在组成的命题中真命题的个数是；(2)、从（1）中选择一个真命题进行证明已知：
求证：
证明：
22. 如图，已知AB∥CD，EF∥MN，∠1=115°，
(1)、求∠2和∠4的度数；(2)、本题隐含着一个规律，请你根据（1）的结果进行归纳：如果一个角的两边分别平行于另一个角的两边，那么这两个角；(3)、利用(2)的结论解答：如果两个角的两边分别平行，其中一个角是另一个角的两倍，求这两个角的大小.23. 探究问题：已知 ， 画一个角 ， 使// ， // ， 且DE交BC于点P．与有怎样的数量关系？
(1)、我们发现与有两种位置关系：如图1与图2所示．①图1中与数量关系为 ▲ ；图2中与数量关系为 ▲ ；选择图1的情况，说明理由．
②由①得出一个真命题，请用文字叙述该命题．
(2)、应用②中的真命题，解决以下问题：若两个角的两边互相平行，且一个角比另一个角的3倍少60°，求出这两个角的度数．24. （概念学习）定义：对于一个三位的自然数 ，各数位上的数字都不为0，且百位数字与十位数字之和除以个位数字的商为整数，则称这个自然数 为“好数”．例如：714是“好数”，因为它是一个三位的自然数，7，1，4都不为0，且 ， ，2为整数；
643不是“好数”，因为 ， 的商不是整数．
(1)、（初步探究）自然数312，675，981，802是“好数”的为；
(2)、在横线上填“真”或“假”：①个位数字为1的一个三位自然数一定是“好数”是命题；
②各数位上的数字都相同的一个三位自然数一定是“好数”是命题；
(3)、（深入思考）求同时满足下列条件的“好数”：
①百位数字比十位数字大5；
②百位数字与十位数字之和等于个位数字．
25. 问题情境：我们知道，“如果两条平行直线被第三条直线所截，截得的同位角相等，内错角相等，同旁内角互补”，所以在某些探究性度量中通过“构造平行线”可以起到转化角的作用．已知三角板ABC中，∠BAC＝60°，∠B＝30°，∠C＝90°，长方形DEFG中，DE//GF．
问题初探：
如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，则∠EMC的度数是多少呢？若过点C作CH//GF，则CH//DE，这样就将∠CAF转化为∠HCA，∠EMC转化为∠MCH，从而可以求得∠EMC的度数为…．
(1)、请你直接写出：∠CAF＝°，∠EMC＝°．(2)、类比再探：若将将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想∠EMC与∠CAF的数量关系？并说明理由．(3)、方法迁移：请你猜想（1）（2）解决问题的思路，在图（2）中探究∠BAG与∠BMD的数量关系？并说明理由．