2022-2023初数北师大版八年级上册7.5 三角形的内角和定理 同步练习
试卷更新日期：2022-09-18 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 在中， ， 则的形状是（ ）A、等腰三角形 B、钝角三角形 C、直角三角形 D、锐角三角形2. 下列说法错误的是（ ）A、有一个内角是直角的三角形是直角三角形 B、一个三角形只能有一个内角是钝角 C、对顶角相等 D、有两个内角是锐角的三角形是锐角三角形3. 已知一个多边形的外角和是其内角和的 ，则下列说法正确的是（ ）A、过这个多边形一个顶点可做7条对角线 B、它的内角和为1260° C、如果将它剪掉一个角，则还余下8个角 D、它的每个外角为40°4. 如果一个三角形有两个外角（不在同一顶点）的和等于270°，则此三角形一定是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形5. 如图：已知 ， BD、CD、BE分别平分的内角、外角、外角 ， 其中点D、C、E在同一条直线上，以下结论：错误的是（ ）
A、 B、 C、 D、6. 下列说法正确的是（ ）A、同位角相等 B、一个角的补角一定是钝角 C、过直线外一点有且只有一条直线与已知直线平行 D、三角形按角的大小分类可分为锐角三角形和钝角三角形7. 下列三角形，不一定是等边三角形的是（ ）A、三个角都相等的三角形 B、有两个角等于60°的三角形 C、边上的高也是这边的中线的三角形 D、有一个外角等于120°的等腰三角形8. 如图，AB⊥AF，∠B、∠C、∠D、∠E、∠F的关系为（ ）
A、∠B+∠C+∠D+∠E+∠F＝270° B、∠B+∠C﹣∠D+∠E+∠F＝270° C、∠B+∠C+∠D+∠E+∠F＝360° D、∠B+∠C﹣∠D+∠E+∠F＝360°9. 如图：CDAB，BC平分∠ACD，CF平分∠ACG，∠BAC=40°，∠1=∠2，则下列结论：①∠ACE=2∠4；②CB⊥CF；③∠1=70°；④∠3=2∠4，其中正确的是（ ）
A、①②③ B、①②④ C、②③④ D、①②③④10. 如图，∠ABD和∠ACE是△ABC的外角，过点B的直线FH和过点C的直线GH相交于点H，且∠DBF＝∠ABD，∠ECG＝∠ACE.设∠A＝α，∠H＝β，则α与β之间的数量关系为（ ）
A、α＋β＝120° B、α＋β＝180° C、α＋β＝120° D、2α＋β＝120°二、填空题（每题3分，共18分）
-
11. △ABC中，已知∠A＝50°，∠B＝60°，则∠C的外角的度数是 ．12. 如图，∠ACD是△ABC的外角，若∠ACD＝120°，∠A＝50°，则∠B＝ ．
13. 三角形的一个外角是100°，则与它不相邻的两内角平分线夹角（钝角）是 .
14. 在中，已知 ， 的形状是 ．15. 如图，铅笔放置在△ABC的边AB上，笔尖方向为点A到点B的方向，把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后，笔尖方向变为点B到点A的方向，这种变化说明 ．
16. 如图，AE∥CF，∠ACF的平分线交AE于点B，G是CF上的一点，∠GBE的平分线交CF于点D，且BD⊥BC，下列结论：①BC平分∠ABG；②AC∥BG；③与∠DBE互余的角有2个；④若∠A＝α，则∠BDF＝180°﹣ ， 其中正确的是 ． （请把正确结论的序号都填上）
三、解答题（共8题，共52分）
-
17. 已知：如图，∠CAE是△ABC的外角，AD∥BC且∠1＝∠2，求证：AB＝AC．
18. 已知：如图，△ABC中，∠B＝∠C，AD是△ABC外角∠EAC的平分线．先猜想AD与BC的位置关系，再进行说理．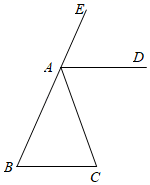
19. 如图，在△ABC中，点D，E分别是AB、AC上一点，若CD、DE分别是∠ACB和∠ADC的角平分线，且DE∥BC，求证：∠DEC + 2∠B = 180°.
20. 如图所示，点E在 外部，点D在BC边上，DE交AC于F，若 ，AD=AB，求证：AC=AE.
21. 如图，已知BD是△ABC的角平分线，CD是△ABC的外角∠ACE的外角平分线，CD与BD交于点D.
(1)、若∠A=50°，则∠D=；(2)、若∠A=80°，则∠D=；(3)、若∠A=130°，则∠D=；(4)、若∠D=36°，则∠A=；(5)、综上所述，你会得到什么结论？证明你的结论的准确性.22. 如图，∠ACD是等边△ABC的一个外角，点E是∠ACD内部任意一点，作直线CE．
(1)、当CE平分∠ACD时，证明：AB∥CE．(2)、已知点A关于直线CE的对称点为F，连接AF、BF、CF，其中AF、BF分别交直线CE于P、Q两点．记∠ACE＝α，当0＜α＜60°时，求∠BFC，（用含α的式子表示）(3)、若（2）中的α满足0°＜α＜120°时，①∠AFB＝ °；
②探究线段QB、QC、QP之间的数量关系，并证明．
23. 当光线经过镜面反射时，入射光线、反射光线与镜面所夹的角对应相等．例如：在图①，有 ， ． 设镜子与的夹角 ．
(1)、如图①，若 ， 判断入射光线与反射光线的位置关系，并说明理由；(2)、如图②，若 ， 设镜子与的夹角（），入射光线与镜面的夹角（），已知入射光线分别从镜面、、反射，反射光线与入射光线平行，请求出与的关系式．24. 第一学习小组按照老师留的预习任务，对如下问题进行了自主探究性学习：已知：如图1所示，在中， ， ， 是的中线，过点C作 ， 垂足为M，且交于点E．
(1)、【探究一：相等的角】同学们用量角器度量后猜想 ， 请你先判断他们的猜想是否符合题意，再用所学知识说明理由；
(2)、【探究二：相等的线段】如图2所示，组员小亮在（1）的条件上添加了一条线段 ， 且平分交于点N，即可得 ， 并给出了说明理由；请你和他共同完成下面的说理过程．
解：如图2中，
因为平分 ， ，
所以 ， （依据： ）
因为 ，
所以 ，
所以 ，
在和中，
因为▲ ， ▲ ， ▲
所以（依据： ），
所以 ． （依据： ）
(3)、【探究三：全等的三角形】如图3所示，组员小刚在（2）的条件上，连接 ， 又发现了一组全等三角形，请直接写出这组全等三角形．