2022-2023初数北师大版八年级上册7.4平行线的性质 同步练习
试卷更新日期:2022-09-18 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,直线 , 直线 , 若 , 则的度数为( )
 A、50° B、45° C、40° D、30°2. 如图,直线a∥b,直线c与直线a,b分别交于点A,B,AD⊥b于点D,若∠1=57°,则∠2的度数为( )
A、50° B、45° C、40° D、30°2. 如图,直线a∥b,直线c与直线a,b分别交于点A,B,AD⊥b于点D,若∠1=57°,则∠2的度数为( )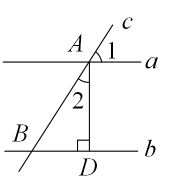 A、30° B、32° C、33° D、40°3. 如图,直线AB∥CD,∠EFB=60°,则∠CGE的度数是( )
A、30° B、32° C、33° D、40°3. 如图,直线AB∥CD,∠EFB=60°,则∠CGE的度数是( )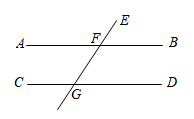 A、130° B、110° C、120° D、60°4. 如图,在四边形中,下列结论正确的是( )
A、130° B、110° C、120° D、60°4. 如图,在四边形中,下列结论正确的是( ) A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 如图,将一副三角板的直角顶点重合,且使 , 则的度数是( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则5. 如图,将一副三角板的直角顶点重合,且使 , 则的度数是( )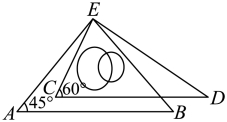 A、 B、 C、 D、6. 如图所示, , , 若 , 则的度数为( )
A、 B、 C、 D、6. 如图所示, , , 若 , 则的度数为( ) A、100° B、110° C、120° D、130°7. 如图,已知直线 , 点B在直线a上,点A,C在直线b上,且 . 若 , 则∠2的度数是( )
A、100° B、110° C、120° D、130°7. 如图,已知直线 , 点B在直线a上,点A,C在直线b上,且 . 若 , 则∠2的度数是( )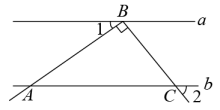 A、45° B、50° C、55° D、60°8. 如图,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3,若图3中∠CFE=120°,则图1中的∠DEF的度数是( )
A、45° B、50° C、55° D、60°8. 如图,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3,若图3中∠CFE=120°,则图1中的∠DEF的度数是( ) A、30° B、20° C、40° D、15°9. 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB.若∠B为锐角,BC∥DF,则∠B的大小为( )
A、30° B、20° C、40° D、15°9. 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB.若∠B为锐角,BC∥DF,则∠B的大小为( )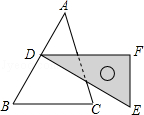 A、30° B、45° C、60° D、75°10. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )
A、30° B、45° C、60° D、75°10. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )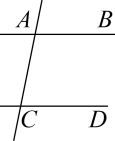 A、③④ B、①③④ C、①②④ D、②③④
A、③④ B、①③④ C、①②④ D、②③④二、填空题(每题3分,共18分)
-
11. 如图,已知直线ab,cd,若∠1、∠2是图中的两个角,且这两个角的两边分别平行, , , 则x值为 .
 12. 如图,已知AB∥CD,BC∥DE,那么∠B +∠D =.
12. 如图,已知AB∥CD,BC∥DE,那么∠B +∠D =.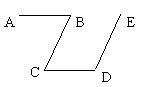 13. 如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是 .
13. 如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是 . 14. 如图, , 若 , , 则的度数为°.
14. 如图, , 若 , , 则的度数为°. 15. 生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,垂直于地面于 , 平行于地面 , 则
15. 生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,垂直于地面于 , 平行于地面 , 则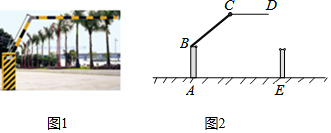 16. 《七彩云南》少数民族传统艺术表演,是七彩云南欢乐世界的王牌演艺节目,它荟萃云南人文之美,深受观众喜爱.在展演中,舞台上的灯光由灯带上位于点和点的两盏激光灯控制.如图,光线与灯带的夹角 , 当光线与灯带的夹角时, .
16. 《七彩云南》少数民族传统艺术表演,是七彩云南欢乐世界的王牌演艺节目,它荟萃云南人文之美,深受观众喜爱.在展演中,舞台上的灯光由灯带上位于点和点的两盏激光灯控制.如图,光线与灯带的夹角 , 当光线与灯带的夹角时, .
三、解答题(共8题,共52分)
-
17. 如图,点P为∠AOB的角平分线OC上的一点,过点P作PM∥OB交OA于点M,过点P作PN⊥OB于点N.当∠AOB=60°时,求∠OPN的度数.

解:∵PN⊥OB于点N,
∴∠PNB= ▲ °( )(填推理的依据).
∵PM∥OB,
∴∠MPN=∠PNB=90°,
∠POB= ▲ ( )(填推理的依据).
∵OP平分∠AOB,且∠AOB=60°,
∴∠POB=∠AOB=30°(角的平分线的定义).
∴∠MPO= ▲ °.
∵∠MPO+∠OPN=∠MPN,
∴∠OPN= ▲ °.
18. 把推理过程补充完整,并填写相应的理由.
如图,∵AC∥EF(已知),
∴ . ( )
. ( )
又∵平分(已知),
∴ ▲ . ( )
∴ . ( )
19. 完成下面的证明:已知:如图,点D,E,F分别是三角形ABC的边 BC、AC、AB上的点,且DE∥BA,DF∥CA.
求证: .
证明:∵DE∥BA
∴ ▲ = ▲ ( )
∵DF∥CA
∴ ▲ = ▲ ( )
∴
20. 完成下面的证明过程,如图,BD∥GF,∠1=∠2.求证:∠DEC=∠ABC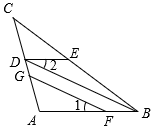
证明:∵BD∥GF( )
∴∠1= ▲ (两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠2= ▲ ( )
∴DE∥AB( )
∴∠DEC=∠ABC( )
21. 阅读下列推理过程,在括号中填写依据.已知:如图,点、分别在线段、上, , , 交于点 , 平分 .
求证:平分 .

证明:∵平分(已知).
∴(角平分线的定义).
∵(已知),
∴( ).
∴(等量代换).
∵(已知),
∴( ).
▲ (两直线平行,内错角相等).
∴( ).
∴平分(角平分线的定义).
22. 数学课上,同学们通过撕、拼的方法,探索、验证三角形的内角和等于180°.下面是小彬的课堂笔记,请阅读操作方法,补全说理过程.如图1,△ABC中的三个内角分别为∠1,∠2,∠3.将∠2和∠3撕下,按图2的方式拼摆,使∠2和∠3的顶点均与∠1的顶点重合,∠2的一边与AB重合,∠3的一边与AC重合.
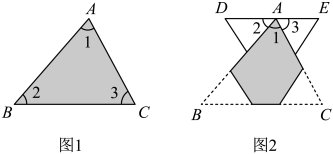
理由:由操作可知∠B=∠2,
所以AD∥ ▲ (依据: ▲ ).
同理,∠C=∠3,
所以, ▲ ∥ ▲ ,
所以,AD、AE在同一直线上,
所以,∠DAE= ▲ ° ,
即 ∠1+ ▲ + ▲ = ▲ .
23. 如图1,点在直线上,点在直线上,平分平分 , 且. (1)、判断直线与的位置关系,并说明理由;(2)、如图2,若为直线上一定点,为直线上一动点,当点在直线上运动时(不与点重合),猜想与之间的数量关系,并说明理由.24. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.
(1)、判断直线与的位置关系,并说明理由;(2)、如图2,若为直线上一定点,为直线上一动点,当点在直线上运动时(不与点重合),猜想与之间的数量关系,并说明理由.24. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.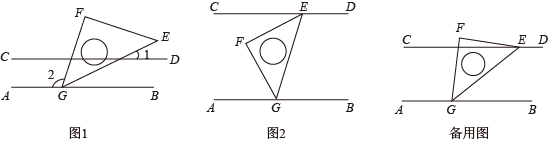 (1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.
(1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.