2022-2023初数北师大版八年级上册7.3平行线的判定 同步练习
试卷更新日期:2022-09-18 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 在下面的四个图形中,已知∠1=∠2,那么能判定AB∥CD的是( )A、
 B、
B、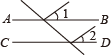 C、
C、 D、
D、 2. 如图,能判定EC∥AB的条件是( )
2. 如图,能判定EC∥AB的条件是( ) A、∠B=∠ACE B、∠A=∠ECD C、∠B=∠ACB D、∠A=∠ACE3. 如图,点E在BA延长线上,下列条件不能判断的是( )
A、∠B=∠ACE B、∠A=∠ECD C、∠B=∠ACB D、∠A=∠ACE3. 如图,点E在BA延长线上,下列条件不能判断的是( ) A、 B、 C、 D、4. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( )
A、 B、 C、 D、4. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( ) A、2个 B、3个 C、4个 D、5个5. 如图,下列条件中,不能判断直线的是( )
A、2个 B、3个 C、4个 D、5个5. 如图,下列条件中,不能判断直线的是( ) A、∠1=∠2 B、∠3=∠4 C、∠4=∠6 D、∠2+∠5=180°6. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线 , , 贝贝、晶晶、欢欢三位同学的做法如图所示:
A、∠1=∠2 B、∠3=∠4 C、∠4=∠6 D、∠2+∠5=180°6. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线 , , 贝贝、晶晶、欢欢三位同学的做法如图所示:
上述三位同学的做法中,依据“内错角相等,两直线平行”的是( )A、仅贝贝同学 B、贝贝和晶晶 C、晶晶和欢欢 D、贝贝和欢欢7. 如图,点E在BC的延长线上,下列条件中能判定CDAB的是()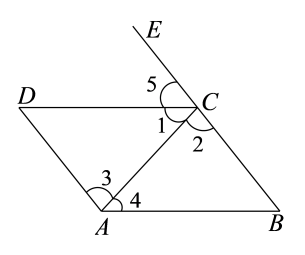
①∠1=∠4②∠2=∠3③∠5=∠B④∠DCB+∠B=180°
A、①②③④ B、①②③ C、①③④ D、①②8. 下列命题错误的是( )A、经过直线外一点,有且只有一条直线与这条直线平行 B、在同一平面内,过一点有且只有一条直线与已知直线垂直 C、连接直线外一点与直线上各点的所有线段中,垂线段最短 D、在同一平面内,垂直于同一条直线的两条直线互相垂直9. 如图,平分 , 平分 , 下列选项能判断∥的是( ) A、 B、 C、 D、10. 如图,给出下列条件:
A、 B、 C、 D、10. 如图,给出下列条件:①∠1=∠3;②∠3=∠5;③∠4+∠7=180°;④∠5+∠3=180°.
能判断a∥b的是( )
 A、①②④ B、①③④ C、①②③④ D、①②
A、①②④ B、①③④ C、①②③④ D、①②二、填空题(每题3分,共18分)
-
11. 如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件有 .
 12. 如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是 .
12. 如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是 .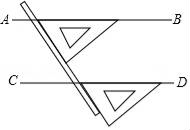 13. 如图,小明在两块按如图所示的方式摆放的含30°角的直角三角板的边缘画直线AB、CD,得到 , 这是根据 , 两直线平行.
13. 如图,小明在两块按如图所示的方式摆放的含30°角的直角三角板的边缘画直线AB、CD,得到 , 这是根据 , 两直线平行.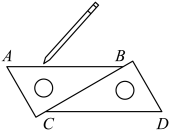 14. 如图,如果 , 那么 .
14. 如图,如果 , 那么 . 15. 如图,要使CDBE , 需要添加的一个条件为: .
15. 如图,要使CDBE , 需要添加的一个条件为: .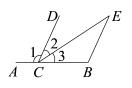 16. 如图,直线AB,CD被直线CE所截, , 请写出能判定AB∥CD的一个条件: .
16. 如图,直线AB,CD被直线CE所截, , 请写出能判定AB∥CD的一个条件: .
三、解答题(共8题,共52分)
-
17. 已知:如图,点E,F是BD上的点,∠AED=∠CFB,AE=CF,BE=DF.
求证:AB∥CD,AB=CD.
 18. 如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: .
18. 如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: .请完成下列推理过程:
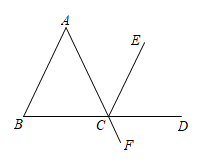
证明:∵CD 平分∠ECF
∴∠ECD= ▲ ( )
∵∠ACB=∠FCD( )
∴∠ECD=∠ACB( )
∵∠B=∠ACB
∴∠B=∠▲( )
∴ ( ).
19. 如图,点E、F分别是直线AB、CD上的点,分别连接AD、EC,交点为G,连接BF,与AD交于点H,若∠1=∠2,∠B=∠C.求证:∠A=∠D.
请根据题意将下面的解答过程补充完整:
解:∵∠1=∠CGD( ),∠1=∠2,
∴∠2=∠CGD,
∴ ▲ ( ),
∴∠B=∠AEG( )
∵∠B=∠C,
∴∠AEG=∠C,
∴ ▲ ( ),
∴∠A=∠D( ).
20. 完成下面的证明:如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.
完成推理过程:
BE平分∠ABD(已知),
∴∠ABD=2∠α( ).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β( )
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( )
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°( ).
∴AB∥CD( ).
21. 如图,已知点在上,平分平分. (1)、试说明:;(2)、若 , 试判断与平行吗?为什么?22. 下面是小明完成“过直线外一点作这条直线的平行线”的尺规作图.
(1)、试说明:;(2)、若 , 试判断与平行吗?为什么?22. 下面是小明完成“过直线外一点作这条直线的平行线”的尺规作图.
已知:直线l及直线l外一点P.
求作:直线PQ,使得// . (不写作法,保留作图痕迹)
如图,直线PQ就是所求直线.
(1)、根据作图痕迹,填空:①AC是的 ▲ , ② ▲ ;
(2)、根据作图痕迹,说明直线PQ与l为什么平行?23. 如图所示,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°. (1)、求证:AB∥CD;(2)、试猜想∠2与∠3的数量关系,并说明理由.24. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°)
(1)、求证:AB∥CD;(2)、试猜想∠2与∠3的数量关系,并说明理由.24. 三角板是学习数学的重要工具 ,将一副三角板的直角顶点 C 按如图所示的方式叠放在一起, 当 时 ,且点 E 在直线AC 的上方时, 解决下列问题∶ (友情提示 ∶ ∠A=60°,∠D=30°,∠B=∠E=45°) (1)、①若 ∠DCE=45°,求∠ACB;
(1)、①若 ∠DCE=45°,求∠ACB;②若∠ACB=140°,求∠DCE ;
(2)、由(1)猜想 ∠ACB与∠DCE的数量关系,并说明理由;(3)、这两块三角板是否存在一组边互相平行?若存在,请直接写出∠ACE的所有可能的值(不必说明理由);若不存在,请说明理由.