2022-2023初数北师大版八年级上册第六章数据的分析 章末检测

试卷更新日期：2022-09-18 类型：单元试卷

进入 出卷网 下载

一、单选题（每题3分，共30分）

  • 1. 一组数据：5，7，6，3，4的平均数是（  ）
    A、5 B、6 C、4 D、8

    查看试题解析

  • 2. 某公司招聘大堂经理，考核项目为个人形象、交际能力、专业知识三个项目，并按2：4：4的权重计算出个人最终得分．某应聘者三项得分依次为80，85，90，则他的最终得分是（　　）
    A、85 B、86 C、87 D、88

    查看试题解析

  • 3. 某次文艺汇演中若干名评委对九（1）班节目给出评分，在计算中去掉一个最高分和最低分．这种操作，对数据的下列统计量一定不会影响的是（    ）
    A、平均数 B、中位数 C、众数 D、方差

    查看试题解析

  • 4. 某校10名学生参加“交通安全”知识测试，他们得分情况如表中所示，则这10名学生所得分数的众数和中位数分别是（  ）

    A、95和85 B、90和85 C、90和87.5 D、85和87.5

    查看试题解析

  • 5. 某校“啦啦操”兴趣小组共有50名学生，她们的年龄分布如下表：

    年龄/岁

    12

    13

    14

    15

    人数

    5

    23

    ■

    ■

    由于表格污损，14岁、15岁人数看不清，则下列关于年龄的统计量可以确定的是（  ）．

    A、平均数、众数 B、众数、中位数 C、平均数、中位数 D、中位数、方差

    查看试题解析

  • 6. 一组数据：-1，1，3，4，a，若它们的平均数为2，则这组数据的众数为（        ）
    A、1 B、2 C、3 D、4

    查看试题解析

  • 7. 一组数据：a1 ， a2 ， ⋅⋅⋅ ， an的平均数为P ， 众数为Z ， 中位数为W ， 则以下判断正确的是（  ）
    A、P一定出现在a1 ， a2 ， ⋅⋅⋅ ， an中 B、Z一定出现在a1 ， a2 ， ⋅⋅⋅ ， an中 C、W一定出现在a1 ， a2 ， ⋅⋅⋅ ， an中 D、P ， Z ， W都不会出现在a1 ， a2 ， ⋅⋅⋅ ， an中

    查看试题解析

  • 8. 甲、乙两人在相同条件下进行射击练习，每人10次射击成绩的平均数都是8环，方差分别是S甲2=0.4 ， S乙2=1.5 ， 则两人射击成绩波动情况是（  ）
    A、甲波动大 B、乙波动大 C、甲、乙波动一样大 D、无法比较

    查看试题解析

  • 9. 已知一组数据a，b，c的平均数为10，方差为4，那么数据a−3 ， b−3 ， c−3的平均数和方差分别是（  ）
    A、10，4 B、7，4 C、3，1 D、7，1

    查看试题解析

  • 10. 跳远运动员李强在一次训练中，先跳了6次的成绩如下：7.6，7.8，7.7，7.8，8.0，7.9（单位：m）．这六次成绩的平均数为7.8，方差为160 ． 如果李强再跳两次，成绩分别为7.6，8.0，则李强这8次跳远成绩与前6次的成绩相比较，其方差 （  ）．
    A、变大 B、变小 C、不变 D、无法确定

    查看试题解析

二、填空题（每题4分，共24分）

  • 11. 如图是小明某一天测得的7次体温情况的折线统计图，这组数据的中位数是 ．

    查看试题解析

  • 12. 从－1，0， 12 ，2中任取两个不同的数求积，不同算式构成的积的众数是 ．

    查看试题解析

  • 13. 已知一组数据x1 ， x2 ， x3 ， x4 ， x5的平均数是3，则数据2x1−1 ， 2x2−1 ， 2x3−1 ， 2x4−1 ， 2x5−1的平均数是 ．

    查看试题解析

  • 14. 北京冬奥会金牌榜前十位的金牌数分别为16，12，9，8，8，8，7，7，6，5．这组数据的平均数、众数和中位数中，最大的是 ．

    查看试题解析

  • 15. 学校举行演讲比赛，共有15名同学进入决赛，比赛将评出金奖1名，银奖3名，铜奖4名．某参赛选手知道自己的分数后，要判断自己能否获奖，他应当关注的有关 成绩的统计量是 （填“平均数”、“中位数”或“众数”）．

    查看试题解析

  • 16. 现有5名同学的身高分别为165，172，168，170，175（单位：厘米）．增加1名身高为170的同学后，这6名同学身高的平均数和方差与原来相比，平均数（填“变大”、“变小”“不变”），方差（填“变大”、“变小”、“不变”）．

    查看试题解析

三、解答题（共8题，共66分）

  • 17. 一组数据从小到大顺序排列后为：1，4，6，x，其中位数和平均数相等，求x的值．

    查看试题解析

  • 18. 某篮球队对队员进行定点投篮测试，每人每天投篮10次，现对甲队员在五天中进行球数（单位：个）进行统计，结果如表：

    甲

    7

    9

    7

    8

    9

    求甲进球的平均数和方差.

    查看试题解析

  • 19. 随机抽取某小吃店一周的营业额（单位：元）如下表：

    星期一

    星期二

    星期三

    星期四

    星期五

    星期六

    星期日

    合计

    540

    680

    640

    640

    780

    1110

    1070

    5460
    (1)、分析数据，填空：这组数据的平均数是元，中位数是元，众数是元．
    (2)、估计一个月的营业额（按30天计算）：

    ①星期一到星期五营业额相差不大，用这5天的平均数估算合适么？

    答（填“合适”或“不合适”）：▲ ．

    ②选择一个你认为最合适的数据估算这个小吃店一个月的营业额．

    查看试题解析

  • 20. 从甲、乙两个企业随机抽取部分职工，对某个月收入情况进行调查，并把调查结果分别制成扇形统计图和条形统计图．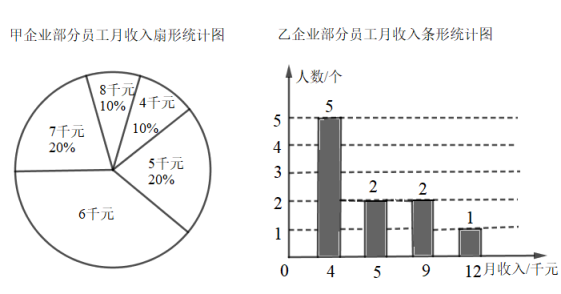

    (1)、在扇形统计图中，“6千元”所在的扇形的圆心角是；
    (2)、在调查人数中，比较甲企业的平均工资与乙企业的平均工资大小时，小明提出自己的看法：虽然不知道甲企业的调查人数，但是由加权平均数的定义，可以计算甲企业的平均工资，因此可以比较，小明的说法符合题意吗？若符合题意，请比较甲企业的平均工资与乙企业的平均工资大小．

    查看试题解析

  • 21. 某校八年级学生开展踢键子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：


    1号

    2号

    3号

    4号

    5号

    总数

    甲班

    120

    118

    130

    109

    123

    600

    乙班

    109

    120

    115

    139

    117

    600

    经统计发现两班总数相等，此时有学生建议，可以通过考查数据中的其他信息作为参考．请你回答下列问题：

    (1)、填空：甲班的优秀率为 ， 乙班的优秀率为；
    (2)、填空：甲班比赛数据的中位数为 ， 乙班比赛数据的中位数为；
    (3)、根据以上两条信息，你认为应该把冠军奖杯发给哪一个班级？简述你的理由．

    查看试题解析

  • 22. 某校为了改善学生伙食，准备午餐为学生提供鸡腿．现有A、B两家副食品厂可以提供规格为75g的鸡腿，而且它们的价格相同，品质也相近．质检人员分别从两家随机各抽取10个，记录它们的质量（单位：g）如下：

    A加工厂 74   74   74   75   73   77   78   72   76   77

    B加工厂 78   74   77   73   75   75   74   74   75   75

    并对以上数据进行整理如下：


    平均数

    中位数

    众数

    方差

    A加工厂

    75

    74.5

    b

    3.4

    B加工厂

    75

    a

    75

    2

    根据以上分析，回答下列问题：

    (1)、统计表中a= ， b=；
    (2)、根据以上信息估计B加工厂加工的100个鸡腿中，质量为75g的鸡腿有多少个？
    (3)、如果考虑鸡腿的规格，学校应该选购哪家加工厂的鸡腿？说明理由．

    查看试题解析

  • 23. 近年来网约车给人们的出行带来了便利．八年级张亮同学对“美团”和“滴滴”两家网约车公司司机月收入进行了一项抽样调查，两家公司分别抽取的10名司机月收入（单位：千元）如图所示：

    根据以上信息，整理分析数据如下：


    平均月收入

    中位数

    众数

    方差

    “美团”

    6

    a

    b

    1.2

    “滴滴”

    6

    4.5

    4

    c

    (1)、填空：a=；b=；c=；
    (2)、张亮的叔叔决定从两家公司中选择一家做网约车司机，如果你是张亮，你建议他选哪家公司？请说明理由．

    查看试题解析

  • 24. 某商场统计了每个营业员在某月的销售额，绘制了如下统计图．

    解答下列问题：

    (1)、设营业员的月销售额为x（单位：万元）．商场规定：当x<15时为不称职，当15≤x<20时为基本称职，当20≤x<25时为称职，当x≥25时为优秀．试求出不称职、基本称职、称职、优秀四个层次营业员人数所占百分比，并画出相应的扇形图．
    (2)、根据（1）中规定，所有称职和优秀的营业员月销售额的中位数、众数和平均数分别是多少？
    (3)、为了调动营业员的积极性，决定制定一个月销售额奖励标准，凡达到或超过这个标准的营业员将受到奖励．如果要使得称职和优秀的所有营业员的半数左右能获奖，奖励标准应定为多少元？并简述其理由．

    查看试题解析