2022-2023初数北师大版八年级上册6.4 数据的离散程度 同步练习

试卷更新日期：2022-09-18 类型：同步测试

进入 出卷网 下载

一、单选题（每题3分，共30分）

  • 1. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩平均数均为9环，方差分别为：s甲2=0.56 ， s乙2=0.48 ， s丙2=0.58 ， s丁2=0.52 ， 则成绩最稳定的是（ ）．
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 2. 若x1 ， x2 ， x3 ， ⋯，xn的平均数为8，方差为2，则关于x1＋2，x2＋2，x3＋2，……，xn＋2，下列结论正确的是（  ）
    A、平均数为8，方差为2 B、平均数为8，方差为4 C、平均数为10，方差为2 D、平均数为10，方差为4

    查看试题解析

  • 3. 已知样本数据3，4，6，5，7，下列说法错误的是（ ）
    A、平均数是5 B、方差是2 C、中位数是6 D、标准差是 2

    查看试题解析

  • 4. 在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，参加表演的女演员的身高的平均数（单位：cm）和方差分别为x¯甲=165 ， x¯乙=165 ， s甲2=1.5 ， s乙2=2.5 ， 那么女演员的身高更整齐的是（ ）
    A、甲团 B、乙团 C、两团一样 D、无法确定

    查看试题解析

  • 5. 在方差的计算公式S2=110[(x1−20)2+(x2−20)2+...+(x10−20)2]中，数字10和20表示的意义分别是（  ）
    A、数据得个数和平均数 B、数据的方差和平均数 C、数个数和方差 D、以上都不对

    查看试题解析

  • 6. 用计算器计算方差时，要首先进入统计计算状态，需要按键（    ）
    A、 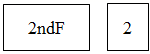B、 C、 D、

    查看试题解析

  • 7. 为了从四名同学中选出一人参加计算机编程比赛，对他们进行了多次测试，并对每个人的测试成绩的平均数及方差进行了统计（如下表），则应选的同学是（  ）

    学生

    学生一

    学生二

    学生三

    学生四

    平均数

    95

    96

    96

    95

    方差

    5

    5

    4.8

    4.8

    A、学生一 B、学生二 C、学生三 D、学生四

    查看试题解析

  • 8. 甲组数据为4、5、6、7；乙组数据为3、5、6、8，下列说法正确的是（   ）
    A、甲更稳定 B、乙更稳定 C、方差一样 D、无法比较

    查看试题解析

  • 9. 将数据a、b、e、d、e、f的每一个数据都增加5，则下列说法中错误的是（   ）
    A、平均数增加5 B、中位数增加5 C、众数增加5 D、方差增加5

    查看试题解析

  • 10. 某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验，它们亩产量的平均数分别是x¯甲=621千克，x¯乙=622千克，方差分别是s甲2=2.6 ， s乙2=28.7 ． 则关于这两种小麦推广种植的合理决策是（       ）
    A、乙的平均亩产量较高，应推广乙 B、甲、乙的平均亩产量相差不多，均可推广 C、甲、乙的平均亩产量相差不多，但甲的亩产量比较稳定，应推广甲 D、乙的平均亩产量较高，且亩产量比较稳定，应推广乙

    查看试题解析

二、填空题（每题3分，共18分）

  • 11. 小明利用公式S2=1n[（5-x）2+（8-x）2+（4-x）2+（7-x）2+（6-x）2]计算5个数据的方差，则这5个数据的标准差S的值是。

    查看试题解析

  • 12. 一组数据2022，2022，2022，2022，2022的方差是 ．

    查看试题解析

  • 13. 甲、乙、丙、丁四位跨栏运动员在某天“110米跨栏”训练中，每人各跑5次，据统计，他们的平均成绩都是13.2秒，甲、乙、丙、丁成绩的方差分别是0.11，0.03，0.05，0.02．则当天这四位运动员“110米跨栏”训练成绩最稳定的是 ．

    查看试题解析

  • 14. 甲、乙二人五次数学考试成绩如下：

    甲：85，84，82，88，86.

    乙：84，85，85，85，86.

    则甲、乙两人成绩比较稳定的是 ．

    查看试题解析

  • 15. 数据x1 ， x2 ， x3 ， x4的平均数是4，方差是3，则数据x1+1 ， x2+1 ， x3+1 ， x4+1的平均数和方差分别是 ， ．

    查看试题解析

  • 16. 有甲、乙两组数据，如表所示：甲、乙两组数据的方差分别为s甲2 ， s乙2 ， 则s甲2s乙2（填“>”，“<”或“=”）.

    甲

    10

    12

    13

    14

    16

    乙

    12

    12

    13

    14

    14

    查看试题解析

三、解答题（共8题，共52分）

  • 17. 某排球队6名场上队员的身高（单位：cm）是180，184，188，190，192，194.现用一名身高为186cm的队员换下场上身高为192cm的队员，与换人前相比，场上队员身高的方差会变化吗？通过计算说明你的理由。

    查看试题解析

  • 18. 某学校为选拔数学能力突出的学生参加中学生数学竞赛，组织了多次测试，其中甲乙两位同学成绩较为优秀，他们在六次赛前测试中的成绩（单位：分）如下表所示．

    甲

    80

    75

    90

    64

    88

    95

    乙

    84

    80

    88

    76

    79

    85

    如果根据这六次成绩选拔其中一人参加比赛，你认为哪一位比较合适？为什么？

    查看试题解析

  • 19. 某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛，其预赛成绩如图所示：

    (1)、根据上图填写下表：


    平均数

    众数

    中位数

    方差

    甲班

    8.5

    8.5

    0.7

    乙班

    8.5

    8

    1.6

    (2)、请你分别从平均数、众数、中位数和方差四个方面评价甲、乙两班的预赛成绩，并说明你的理由；
    (3)、乙班小明说：“我的成绩是中等水平”，你知道他是几号选手？

    查看试题解析

  • 20.

    某农村初中2013年、2014年分别选拔了7名同学参加县级“综合体能”竞赛，学校想了解今年（2014年）7位同学实力，于是在3月1日进行一次与去年项目、评分方法完全一样的测试．两年成绩如下表：

    2013年

    58

    65

    70

    70

    70

    75

    82

    2014年

    50

    55

    70

    75

    78

    80

    82

    （1）请根据表中数据补全条形统计图；

    （2）分别求出两年7位同学成绩的中位数和平均成绩；

    （3）经计算2014的7位同学成绩的方差S2=136.9，那么哪年的7位同学的成绩较为整齐？通过计算说明；

    （4）除上述问题（2），（3）外，根据题中情境由你提出一个问题，并给予解答．

    方差计算公式：S2=1nx1-x-2+x2-x-2+xn-x-3 ．

    查看试题解析

  • 21. 某学校组织七、八年级全体学生举行了安全知识竞赛活动，为了解竞赛成绩情况，为两个年级各随机抽取10名学生的成绩（满分为100分）进行了分析，并依据分析结果绘制了如下表所示的不完整统计表：

    七年级：90，95，95，80，85，90，80，90，85，100；

    八年级：85，85，95，80，95，90，90，90，100，90．

    年级

    平均数

    中位数

    众数

    方差

    七年级

    89

    m

    90

    39

    八年级

    n

    90

    p

    q

    根据以上信息解答下面问题：

    (1)、填空：m＝　   　 ， p＝ 　   　；
    (2)、求q的值；
    (3)、通过数据分析，你认为哪个年级的成绩比较好？说明理由．

    查看试题解析

  • 22. 某市射击队甲、乙两名队员在相同的条件下各射靶10次，每次射靶的成绩情况如图所示：

    (1)、请将表格补充完整：（参考公式：方差S2=1n[(x1−x¯)2+(x2−x¯)2+⋯+(xn−x¯)2]）


    平均数

    方差

    中位数

    甲

    7

    ①

    7

    乙

    ②

    5.4

    ③

    (2)、请从下列三个不同的角度对这次测试结果进行分析：①从平均数和方差相结合看，的成绩好些；②从平均数和中位数相结合看，的成绩好些；
    (3)、若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．

    查看试题解析

  • 23. 为了加强心理健康教育，某校组织七年级（1）（2）两班学生进行了心理健康常识测试（分数为整数，满分为10分），已知两班学生人数相同，根据测试成绩绘制了如下所示的统计图．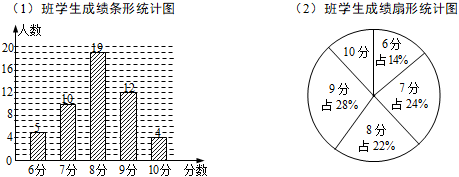

    (1)、求（2）班学生中测试成绩为10分的人数；
    (2)、请确定下表中a，b，c的值（只要求写出求a的计算过程）；

    统计量

    平均数

    众数

    中位数

    方差

    （1）班

    8

    8

    c

    1.16

    （2）班

    a

    b

    8

    1.56

    (3)、从上表中选择合适的统计量，说明哪个班的成绩更均匀．

    查看试题解析

  • 24. 甲乙两人在相同的条件下各射击10次，每次射击的成绩情况如图所示．（方差的计算公式：s2＝ 1n [（x1﹣ x¯ ）2+（x2﹣ x¯ ）2+……+（xn﹣ x¯ ）2]．）

    (1)、请你填写甲的相关数据：

    平均数

    众数

    方差

    甲
    (2)、如果甲第11次射击的成绩是8环，则甲得分中的三个统计量，即平均数、众数、方差发生哪些变化？
    (3)、根据甲、乙10次射击的成绩，如果教练选择甲参加射击比赛，教练的理由是什么？如果教练选择乙参加射击比赛，教练的理由又是什么？

    查看试题解析