2022-2023初数北师大版八年级上册第五章二元一次方程组章末检测

试卷更新日期：2022-09-18 类型：单元试卷

进入出卷网下载

一、填空题（每题4分，共24分）

1. 请写出一个二元一次方程组，使它的解为 ${\begin{cases} x = 1 \\ y = - 1 \end{cases}$ ．

查看试题解析
2. 若关于x，y的二元一次方程组 ${\begin{array}{l} 2 x - y = 3 m + 4 \\ x + 4 y = 2 - m \end{array}$ 的解x，y互为相反数，则m的值为．

查看试题解析
3. 已知一次函数的图象 $y = k x - 2$ 与直线 $y = 3 x + 4$ 平行，则k＝．

查看试题解析
4. 《九章算术》是我国古代一部著名的算书，它的出现标志着中国古代数学形成了完整的体系．其中卷八方程[七]中记载：“今有牛五、羊二，直金八两．牛二、羊五，直金六两．牛、羊各一只直金几何？”题目大意是：5头牛、2只羊共值金8两.2头牛、5只羊共值金6两.1头牛和1只羊值金两．

查看试题解析
5. 问题解决：糖葫芦一般是用竹签串上山楂．再蘸以冰糖制作而成，现将一些山楂分别串在若干个竹签上，如果每根竹签串4个山楂，还剩余3个山楂；如果每根竹签串7个山楂，还剩余6根竹签，求竹签有多少根？山楂有多少个？反思归纳：现有m根竹签，n个山楂，若每根竹签串a个山楂，还剩b个山楂，则m、n、a、b满足的等量关系为（用含m、n、a、b的代数式表示）．

查看试题解析
6. 定义一种新运算“※”，规定 $x ※ y = a x + b y^{2}$ ，其中 $a ， b$ 为常数，等式右边是通常的加法、乘法和乘方运算.若 $1 ※ 2 = 5 ， 2 ※ 1 = 6$ ，则 $2 ※ 3 =$ .

查看试题解析

二、解答题（共9题，共66分）

7. 解方组：

(1)、 ${\begin{array}{l} 2 x + y = 4 \\ x = y - 1 \end{array}$ ；

(2)、 $\frac{s + 2 t}{3} = \frac{3 s - t}{2}$ ＝3；

(3)、 ${\begin{array}{l} x + 2 y + z = 0 \\ 2 x - y - z = 1 \\ 3 x - y - z = 2 \end{array}$

查看试题解析
8.
解方程组
（1） $\{\begin{matrix} x - 2 y = 5 \\ 5 x + 4 y = - 3 \end{matrix}$
（2） $\{\begin{matrix} x + y = 4 \\ 2 x - y = - 1 \end{matrix}$ （用作图方法求解）

查看试题解析
9. 已知方程组 ${\begin{array}{l} 5 x + y = 3 \\ a x + 5 y = 4 \end{array}$ 和 ${\begin{array}{l} x - 2 y = 5 \\ 5 x + b y = 1 \end{array}$ 有相同的解，求 $a - 5 b$ 的平方根．

查看试题解析
10. 甲、乙两人解同一个方程组 ${\begin{array}{l} 3 x + a y = 13 ① \\ b x - 3 y = 9 ② \end{array}$ ，甲因看错①中的a得解为 ${\begin{cases} x = 6 \\ y = 7 \end{cases}$ ，乙因抄错了②中的b解得 ${\begin{cases} x = 1 \\ y = 5 \end{cases}$ ，请求出原方程组的解．

查看试题解析
11. 阅读下列方程组的解法，然后解答相关问题：
解方程组 ${\begin{array}{l} 27 x + 26 y = 25 ① \\ 25 x + 24 y = 23 ② \end{array}$ 时，若直接利用消元法解，那么运算比较繁杂，采用下列解法则轻而易举

解：①-②，得 $2 x + 2 y = 2$ ，即 $x + y = 1$ ． ③

②-③×24，得 $x = - 1$ ．

把 $x = - 1$ 代入③，解得 $y = 2$ ．故原方程组的解是 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ ．

(1)、请利用上述方法解方程组 ${\begin{array}{l} 19 x + 21 y = 23 \\ 11 x + 13 y = 15 \end{array}$ ．

(2)、猜想并写出关于x，y的方程组 ${\begin{array}{l} a x + (a - m) y = a - 2 m \\ b x + (b - m) y = b - 2 m \end{array}$ 的解，并加以检验．

查看试题解析

12. 为了切实保护汉江生态环境，襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后，某水库自然生态养殖的鱼在市场上热销，经销商老李每天从该水库购进草鱼和鲢鱼进行销售，两种鱼的进价和售价如下表所示：

	进价（元/斤）	售价（元/斤）
鲢鱼	$a$	5
草鱼	$b$	销量不超过200斤的部分	销量超过200斤的部分
		8	7

已知老李购进10斤鲢鱼和20斤草鱼需要155元，购进20斤鲢鱼和10斤草鱼需要130元.

(1)、求

a

，

b

的值；

(2)、老李每天购进两种鱼共300斤，并在当天都销售完，其中销售鲢鱼不少于80斤且不超过120斤，设每天销售鲢鱼

x

斤（销售过程中损耗不计）.

①分别求出每天销售鲢鱼获利 $y_{1}$ （元），销售草鱼获利 $y_{2}$ （元）与 $x$ 的函数关系式，并写出 $x$ 的取值范围；

②端午节这天，老李让利销售，将鲢鱼售价每斤降低 $m$ 元，草鱼售价全部定为7元斤，为了保证当天销售这两种鱼总获利 $W$ （元）的最小值不少于320元，求 $m$ 的最大值.

查看试题解析

13. 为了响应“阳光运动一小时”校园体育活动，我校计划再购买一批篮球，已知购买2个A品牌的篮球和3个B品牌的篮球共需380元；购买4个A品牌的篮球和2个B品牌的篮球共需360元．

(1)、求A、B两种品牌的篮球的单价．

(2)、我校打算网购20个A品牌的篮球和3个B品牌的篮球，“双十一”期间，京东购物打折促销，其中A品牌打八折，B品牌打九折，问：学校购买打折后的篮球所花的费用比打折前节省了多少钱？

查看试题解析
14. 如图，某化工厂与A，B两地有公路和铁路相连，这家工厂从A地购买一批每吨1 000元的原料运回工厂，制成每吨8 000元的产品运到B地．已知公路运价为1.5元/（吨•千米），铁路运价为1.2元/（吨•千米），这两次运输共支出公路运费15 000元，铁路运费97 200元，请计算这批产品的销售款比原料费和运输费的和多多少元？
根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：
甲： ${\begin{matrix} 1.5 (20 x + 10 y) = \\ 1.2 (110 x + 120 y) = \end{matrix}$
乙： ${\begin{matrix} 1.5 (20 \times \frac{x}{8000} + 10 \times \frac{y}{1000}) = \\ 1.2 (110 \times \frac{x}{8000} + 120 \times \frac{y}{1000}) = \end{matrix}$

(1)、根据甲，乙两名同学所列方程组，请你分别指出未知数x，y表示的意义，然后在等式右边的方框内补全甲、乙两名同学所列方程组．
甲：x表示，y表示
乙：x表示，y表示

(2)、甲同学根据他所列方程组解得x=300，请你帮他解出y的值，并解决该实际问题．

查看试题解析
15. （活动回顾）：七年级下册教材中我们曾探究过“以方程x+y＝5的解为坐标（x的值为横坐标、y的值为纵坐标）的点的特性”，了解了二元一次方程的解与其图象上点的坐标的关系．
发现：以方程x+y＝5的解为坐标的所有点组成的图象与一次函数y=-x+5的图像相同，是同一条直线；

结论：一般的，以一个二元一次方程的解为坐标的点组成的图像与相应的一次函数的图象相同，是一条直线．

示例：如图1，我们在画方程 $x - y = 5$ 的图象时，可以取点 $A (- 1 ， - 1)$ 和 $B (2 ， 2)$ ，作出直线AB ．

（解决问题）：

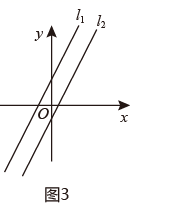
(1)、请你在图2所给的平面直角坐标系中画出二元一次方程组 ${\begin{matrix} 2 x + y = 4 \\ x - y = - 1 \end{matrix}$ 中的两个二元一次方程的图象（提示：依据“两点确定一条直线”，画出图象即可，无需写过程）

(2)、观察图象，两条直线的交点坐标为，由此你得出这个二元一次方程组的解是；

(3)、已知二元一次方程ax+by＝6的图象经过两点A（﹣1，3）和B（2，0），试求a、b的值．

(4)、在同一平面直角坐标系中，一次函数y=2x+2图像l₁和一次函数y=2x-1的图像l₂ ，如图3所示，
①请判断l₁和l₂的关系，并说明理由；

②根据图像，请直接判断方程组 ${\begin{array}{l} 2 x - y = - 2 \\ 2 x - y = 1 \end{array}$ 的解的情况（不需要说明理由）.

查看试题解析

2022-2023初数北师大版八年级上册第五章二元一次方程组 章末检测

一、填空题（每题4分，共24分）

二、解答题（共9题，共66分）

2022-2023初数北师大版八年级上册第五章二元一次方程组章末检测