2022-2023初数北师大版八年级上册5.6-5.7同步练习
试卷更新日期:2022-09-18 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 若方程组没有解,则一次函数y=2-x与y=-x的图象必定( )A、重合 B、平行 C、相交 D、无法确定2. 如图,一次函数y=2x+1的图象与y=kx+b的图象相交于点A,则方程组的解是( )
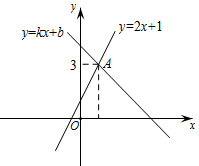 A、 B、 C、 D、3. 如果一次函数y=3x+6与y=2x-4的图象交点坐标为(a,b),则 是方程组( )的解.A、 B、 C、 D、4. 已知方程组的解为 , 则直线y=﹣x+2与直线y=2x﹣7的交点在平面直角坐标系中位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知一次函数y=k1x+b1和一次函数y1=k2x+b2的自变量x与因变量y1 , y2的部分对应数值如表所示,则关于x、y的二元一次方程组的解为( )
A、 B、 C、 D、3. 如果一次函数y=3x+6与y=2x-4的图象交点坐标为(a,b),则 是方程组( )的解.A、 B、 C、 D、4. 已知方程组的解为 , 则直线y=﹣x+2与直线y=2x﹣7的交点在平面直角坐标系中位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知一次函数y=k1x+b1和一次函数y1=k2x+b2的自变量x与因变量y1 , y2的部分对应数值如表所示,则关于x、y的二元一次方程组的解为( )x
…
﹣2
﹣1
0
1
2
…
y1
…
﹣1
0
1
2
3
…
y2
…
﹣5
﹣3
﹣1
1
3
…
A、 B、 C、 D、6. 用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( ) A、 B、 C、 D、7. 已知直线 交x轴于点 ,交 轴于点 ,直线 与直线 关于x轴对称,将直线 向下平移8个单位得到直线 ,则直线 与直线 的交点坐标为( )A、 B、 C、 D、8. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、
A、 B、 C、 D、7. 已知直线 交x轴于点 ,交 轴于点 ,直线 与直线 关于x轴对称,将直线 向下平移8个单位得到直线 ,则直线 与直线 的交点坐标为( )A、 B、 C、 D、8. 一次函数 与正比例函数 (m,n为常数、且 )在同一平面直角坐标系中的图可能是( )A、 B、
B、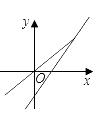 C、
C、 D、
D、 9. 无论m为何实数.直线与的交点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 一次函数y1=ax+b与y2=cx+d的图像如图所示,下列结论中正确的有( )
9. 无论m为何实数.直线与的交点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 一次函数y1=ax+b与y2=cx+d的图像如图所示,下列结论中正确的有( )①对于函数y=ax+b来说,y随x的增大而减小②函数y=ax+d的图像不经过第一象限③④
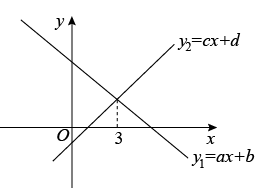 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每空2分,共14分)
-
11. 已知一次函数y=ax+b和y=kx的图象交于点P(﹣4,2),则关于x、y的二元一次方程组 的解是.12. 如图,直线l1:y=x+1与x轴交于点A,与直线l2:y= x+2交于点B,点C为x轴上的一点,若△ABC为直角三角形,则点C的横坐标为 .
 13. 一次函数y1=kx-1(k是常数,且k≠0)和y2=x+1图象的交点始终在第三象限,则k的取值范围是.14. 如图,在同一平面直角坐标系中,直线l1:yx与直线l2:y=kx+3相交于点A,则方程组的解为 .
13. 一次函数y1=kx-1(k是常数,且k≠0)和y2=x+1图象的交点始终在第三象限,则k的取值范围是.14. 如图,在同一平面直角坐标系中,直线l1:yx与直线l2:y=kx+3相交于点A,则方程组的解为 . 15. 如果方程组 无解,那么直线 不经过第象限.16. 直线 与 平行,且经过点(2,1),则k= b=
15. 如果方程组 无解,那么直线 不经过第象限.16. 直线 与 平行,且经过点(2,1),则k= b=三、解答题(共14题,共)
-
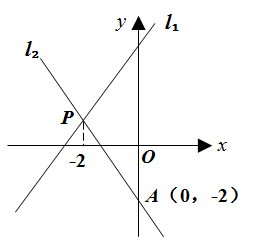
17. 一次函数的图象经过点 和 两点.(1)、求这个一次函数的表达式;(2)、线段 与第一象限的角平分线交于点 ,则点 的坐标为.18. 如图,直线 , 相交于点 ,直线 的函数表达式为 ,点 的横坐标为 ,且直线 与 轴交于点 ,求直线 的函数表达式.
 19. 阅读材料,回答以下问题:
19. 阅读材料,回答以下问题:我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.例如是方程的一个解,对应点 , 如图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点 , , , , 将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程的解.所以,我们就把这条直线就叫做方程的图象.一般的,以任意二元一次方程解为坐标的对应点连成的直线就叫这个方程的图象.请问:
 (1)、已知、、 , 则点(填“或或”)在方程的图象上.(2)、求方程和方程图象的交点坐标.(3)、已知以关于、的方程组的解为坐标的点在方程的图象上,求的值.20. 如图,正比例函数 的图象与一次函数 的图象交于点 ,一次函数图象经过点 ,与y轴的交点为D,与x轴的交点为C.
(1)、已知、、 , 则点(填“或或”)在方程的图象上.(2)、求方程和方程图象的交点坐标.(3)、已知以关于、的方程组的解为坐标的点在方程的图象上,求的值.20. 如图,正比例函数 的图象与一次函数 的图象交于点 ,一次函数图象经过点 ,与y轴的交点为D,与x轴的交点为C.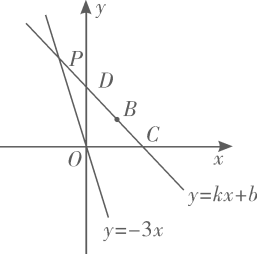 (1)、求一次函数表达式;(2)、求D点的坐标;(3)、求 的面积.(4)、不解关于x、y的方程组 ,直接写出方程组的解.21. 在一条笔直的公路旁依次有 、 、 三个村庄,甲、乙两人同时分别从 、 两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向 村,最终到达 村.设甲、乙两人到 村的距离 , 与行驶时间 之间的函数关系如图所示,请回答下列问题:
(1)、求一次函数表达式;(2)、求D点的坐标;(3)、求 的面积.(4)、不解关于x、y的方程组 ,直接写出方程组的解.21. 在一条笔直的公路旁依次有 、 、 三个村庄,甲、乙两人同时分别从 、 两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向 村,最终到达 村.设甲、乙两人到 村的距离 , 与行驶时间 之间的函数关系如图所示,请回答下列问题: (1)、 、 两村间的距离为 , ;(2)、求出甲、乙两人到 村的距离 , 与行驶时间 之间的函数关系式,并求出图中点 的坐标;(3)、乙在行驶过程中,何时距甲 ?22. 为了积极助力脱贫攻坚工作,如期打赢脱贫攻坚战,某驻村干部带领村民种植草莓,在每年的草莓成熟期都会吸引很多人到果园去采摘.现有甲、乙两家果园可供采摘,这两家草莓的品质相同,售价均为每千克30元,但是两家果园的采摘方案不同.
(1)、 、 两村间的距离为 , ;(2)、求出甲、乙两人到 村的距离 , 与行驶时间 之间的函数关系式,并求出图中点 的坐标;(3)、乙在行驶过程中,何时距甲 ?22. 为了积极助力脱贫攻坚工作,如期打赢脱贫攻坚战,某驻村干部带领村民种植草莓,在每年的草莓成熟期都会吸引很多人到果园去采摘.现有甲、乙两家果园可供采摘,这两家草莓的品质相同,售价均为每千克30元,但是两家果园的采摘方案不同.甲果园:每人需购买20元的门票一张,采摘的草莓按6折优惠;
乙果园:不需要购买门票,采摘的草莓按售价付款不优惠.
设小明和爸爸妈妈三个人采摘的草莓数量为 千克,在甲、乙果园采摘所需总费用分别为 、 元,其函数图象如图所示.

(1)、请分别求出 、 与 之间的函数关系式;(2)、请求出图中点A的坐标并说明点A表示的实际意义;(3)、请根据函数图象,直接写出小明一家选择哪家果园采摘更合算.23. 定义:我们把一次函数与正比例函数的交点称为一次函数的“不动点”.例如求的“不动点”;联立方程 , 解得 , 则的“不动点”为 .(1)、由定义可知,一次函数的“不动点”为 .(2)、若一次函数的“不动点”为 , 求m、n的值.(3)、若直线与x轴交于点A,与y轴交于点B,且直线上没有“不动点”,若P点为x轴上一个动点,使得 , 求满足条件的P点坐标.