安徽省宣城市三校2022-2023学年高二上学期数学期初联考试卷

试卷更新日期：2022-09-16 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | 2 x^{2} + 2 < 5 x} ， B = {y | y = x^{2} + 1}$ ，则 $A ∩ B =$ （）

A、 $(0 ， 2)$ B、 $[1 ， 2)$ C、 $(1 ， 2)$ D、 $(\frac{1}{2} ， 1)$

查看试题解析
2. 已知 $a ， b ， c \in R$ ，在下列条件中，使得 $a < b$ 成立的一个充分而不必要条件是（）

A、 $(a - b) c^{2} < 0$ B、 $a^{3} < b^{3}$ C、 $\frac{1}{a} < \frac{1}{b}$ D、 $a^{2} < b^{2}$

查看试题解析
3. 已知某射击运动员每次击中目标的概率都相同.现采用随机模拟的方法估计该运动员射击3次，击中3次的概率：先由计算器输出0到9之间取整数值的随机数，指定0，1表示没有击中目标， $2 ， 3 ， 4 ， 5 ， 6 ， 7 ， 8 ， 9$ 表示击中目标.因为射击3次，故以每3个随机数为一组，代表射击3次的结果.经随机模拟产生了以下20组随机数：
572  029  714  985  034  437  863  964  141  469
037  623  261  804  601  366  959  742  671  428
据此估计，该射击运动员射击3次击中3次的概率约为（       ）

A、0.45 B、0.50 C、0.55 D、0.60

查看试题解析
4. 在 $△ A B C$ 中，角 $A ， B ， C$ 所对的边分别为 $a ， b ， c ， A = \frac{π}{3} ， b = 2 ， c = 3$ ，则 $\frac{a - 2 b + 2 c}{s i n A - 2 s i n B + 2 s i n C}$ 的值等于（）

A、 $\sqrt{21}$ B、 $\frac{2 \sqrt{21}}{3}$ C、 $\frac{4 \sqrt{7}}{3}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析
5. 关于 $x$ 的一元二次不等式 $m x^{2} - 2 m x - 1 ⩽ 0$ 恒成立，则实数 $m$ 的取值范围为（）

A、 $(- \infty ， 0]$ B、 $(- \infty ， 1]$ C、 $[- 1 ， 0)$ D、 $[- 1 ， 0]$

查看试题解析
6. 函数 $f (x) = c o s [\frac{π}{2} (1 - x)] + l o g_{5} x (x > 0)$ 的零点个数为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，在 $▱ A B C D$ 中，M为BC的中点 $\vec{A C} = m \vec{A M} + n \vec{B D}$ ，则 $\frac{m}{n}$ =（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，正四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的上､下底面边长分别为 $2 \sqrt{2} ， 4 ， E ， F ， G ， H$ 分别为 $A B$ ， $B C ， C D ， D A$ 的中点，8个顶点 $E ， F ， G ， H ， A_{1} ， B_{1} ， C_{1} ， D_{1}$ 构成的十面体恰有内切球，则该内切球的表面积为（）

A、 $8 \sqrt{2} π$ B、 $6 \sqrt{2} π$ C、 $4 \sqrt{2} π$ D、 $2 \sqrt{2} π$

查看试题解析

二、多选题

9. 对于任意两个向量 $\vec{a} ， \vec{b}$ ，下列命题正确的是（）

A、 $| \vec{a} + \vec{b} | \leq | \vec{a} | + | \vec{b} |$ B、 $| \vec{a} - \vec{b} | \leq | \vec{a} | - | \vec{b} |$ C、 $| \vec{a} \cdot \vec{b} | \leq | \vec{a} | \cdot | \vec{b} |$ D、若 $| \vec{a} | > | \vec{b} |$ ，则 $\vec{a} > \vec{b}$

查看试题解析
10. 甲､乙两盒中皆装有若干个不同色的小球，从甲盒中摸出一个红球的概率是 $\frac{1}{3}$ ，从乙盒中摸出一个红球的概率是 $\frac{1}{2}$ ，现小明从两盒各摸出一个球，每摸出一个红球得3分，摸出其他颜色小球得0分，下列说法中正确的是（）

A、小明得6分的概率为 $\frac{5}{6}$ B、小明得分低于6分的概率为 $\frac{5}{6}$ C、小明得分不少于3分的概率为 $\frac{5}{6}$ D、小明恰好得3分的概率为 $\frac{1}{2}$

查看试题解析
11. 关于函数 $f (x) = s i n (x + \frac{π}{6}) s i n x - \frac{\sqrt{3}}{4}$ ，下列说法中错误的是（）

A、其表达式可写成 $f (x) = - c o s (2 x + \frac{π}{6})$ B、曲线 $y = f (x)$ 关于点 $(- \frac{π}{12} ， 0)$ 对称 C、 $y = f (x)$ 在区间 $[\frac{π}{6} ， \frac{π}{3}]$ 上单调递增 D、 $\exists a \in (0 ， \frac{π}{2})$ ，使得 $f (x + a) = f (x + 3 a)$ 恒成立

查看试题解析
12. 若点P在棱长为2的正方体ABCD— $A_{1} B_{1} C_{1} D$ 的表面运动，点M为棱 $A_{1} D_{1}$ 的中点，则下列说法中正确的是（）

A、当点P在底面ABCD内运动时，三棱锥M—ADP体积不变 B、当点P在底面ABCD内运动时，点P到平面 $C_{1} D_{1}$ M的距离不变 C、当直线AP与直线DM所成的角为 $90 °$ 时，线段AP长度的最大值为3 D、当直线AP与直线BB1所成的角为 $45$ °时，点P的轨迹长度为π

查看试题解析

三、填空题

13. 设 $z = \frac{2}{1 - i} + i$ （其中 $i$ 为虚数单位），则 $| z | =$ .

查看试题解析
14. 已知幂函数 $f (x)$ 的图象过点 $(2 ， \frac{1}{4})$ ，则 $f (\sqrt{7}) =$ .

查看试题解析
15. 已知点 $P$ 在 $△ A B C$ 的边 $B C$ 上， $A P = P C = C A = 2 ， △ A B C$ 的面积为 $3 \sqrt{3}$ ，则 $s i n ∠ P A B =$ .

查看试题解析
16. 设 $f (x)$ 的定义域为 $R$ ，且满足 $f (1 - x) = f (1 + x) ， f (x) + f (- x) = 2$ ，若 $f (1) = 3$ ，则 $\frac{f (1) + f (2) + f (3) + ⋯ + f (2022)}{f (2023) + f (2028) + f (2030)} =$ .

查看试题解析

四、解答题

17. 在△ABC中，角A，B，C所对的边分别为a，b，c，且 $b c o s \frac{A}{2} = a s i n B ．$

(1)、求角A的大小；

(2)、若 $b = a + 1 ， c = a - 2$ ，求cosB的值．

查看试题解析
18. 某班20位女同学平均分为甲､乙两组，她们的美学鉴赏课考试成绩如下（单位：分）：
甲组： $65 ， 90 ， 85 ， 75 ， 65 ， 70 ， 75 ， 90 ， 95 ， 80$
乙组： $84 ， 95 ， 75 ， 70 ， 85 ， 80 ， 85 ， 65 ， 90 ， 81$

(1)、试分别计算两组数据的极差和方差；

(2)、试根据（1）中的计算结果，判断哪一组的成绩较稳定？

查看试题解析
19. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ ， $F$ 分别是线段 $A_{1} B_{1}$ ， $B C$ 的中点.

(1)、证明： $E F ∥$ 平面 $A A_{1} C_{1} C$ ；

(2)、若 $A B = B C = 2$ ，直线 $E F$ 与 $B B_{1}$ 所成角的余弦值是 $\frac{\sqrt{3}}{3}$ ，求四面体 $B E F B_{1}$ 的体积.

查看试题解析
20. 读书可以增长知识，开拓视野，修身怡情.树人中学为了解本校学生课外阅读情况，按性别进行分层，用分层随机抽样的方法从全校学生中抽出一个容量为100的样本，其中男生40名，女生60名.经调查统计，分别得到40名男生一周课外阅读时间（单位：小时）的频数分布表和60名女生一周课外阅读时间（单位：小时）的频率分布直方图.
男生一周阅读时间频数分布表
小时
频数
$[0 ， 2)$
9
$[2 ， 4)$
25
$[4 ， 6)$
3
$[6 ， 8)$
3

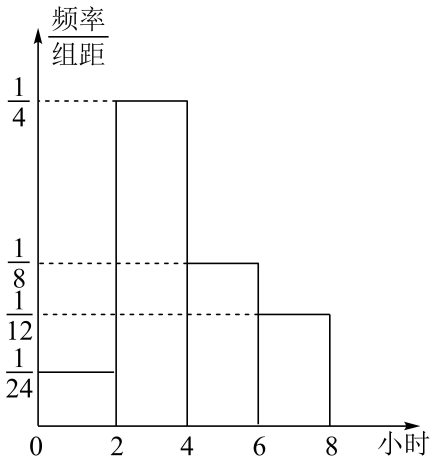(1)、由以上频率分布直方图估计该校女生一周阅读时间的众数和75%分位数；

(2)、由以上频数分布表和频率分布直方图估计总样本的平均数 $\bar{z}$ ；

(3)、从一周课外阅读时间为 $[4 ， 6)$ 的样本学生中按比例分配抽取6人，再从这6人中任意抽取2人，求恰好抽到一男一女的概率.
（注：以各组的区间中点值代表该组的各个值）

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $A B = 3$ ， $A D = \sqrt{5}$ ， $△ B C D$ 是以 $D$ 为直角顶点的等腰直角三角形， $∠ B A D = θ$ ， $θ \in (\frac{π}{2} ， π)$

(1)、当 $c o s θ = - \frac{\sqrt{5}}{5}$ 时，求 $c o s ∠ A D C$ 及 $A C$ ；

(2)、当四边形 $A B C D$ 的面积取最大值时，求 $△ B C D$ 的面积.

查看试题解析
22. 如图，在直角梯形 $A B C D$ 中， $A B ∥ D C$ ， $∠ A B C = 90 °$ ， $A B = 2 D C = 2 B C$ ， $E$ 为 $A B$ 的中点，沿 $D E$ 将 $△ A D E$ 折起，使得点 $A$ 到点 $P$ 的位置，且 $P E ⊥ E B$ ， $M$ 为 $P B$ 的中点， $N$ 是 $B C$ 上的动点（与点 $B$ ， $C$ 不重合）．

(1)、证明：平面 $E M N ⊥$ 平面 $P B C$ ；

(2)、是否存在点 $N$ ，使得二面角 $B - E N - M$ 的正切值为 $\sqrt{5}$ ？若存在，确定 $N$ 点位置；若不存在，请说明理由．

查看试题解析

男生一周阅读时间频数分布表
小时	频数
$[0 ， 2)$	9
$[2 ， 4)$	25
$[4 ， 6)$	3
$[6 ， 8)$	3